2012届高考数学文科一轮复习精选课件(新人教a版):第5章 不等5.3 二元一次不等式(组)与简单的线性规划问题
文档属性
| 名称 | 2012届高考数学文科一轮复习精选课件(新人教a版):第5章 不等5.3 二元一次不等式(组)与简单的线性规划问题 |

|
|
| 格式 | rar | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
学案3 二元一次不等式(组)与简单
的线性规划问题
考点1
考点2
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
考点3
考点4
返回目录
考 纲 解 读
二元一次不等式(组)与简单的线性规划问题 1.能从实际问题中抽象出二元一次不等式组.
2.理解二元一次不等式组表示平面的区域,能够准确地画出可行域.
3.能够将实际问题抽象概括为线性规划问题,培养应用线性规划的知识解决实际问题的能力.
4.培养学生运用数学知识解决实际问题的能力,体会数形结合的数学思想.
考 向 预 测
从近几年的高考试题看,高考中常常以选择题、填空题的形式考查二元一次不等式组表示的平面区域的图形形状以及目标函数的最大值或最小值,有时也在解答题中考查线性规划、求函数的最优解等问题.已知目标函数的最值,求约束条件或目标函数中参数的取值问题,是高考的一种考查方向.
返回目录
1.二元一次不等式(组)表示平面区域
作二元一次不等式Ax+By+C>0(或Ax+By+C<0)表示的平面区域的方法步骤:
(1)在平面直角坐标系中作出直线Ax+By+C=0.
(2)在直线的一侧任取一点P(x0,y0),特别地,当C≠0时,常把 作为此特殊点.
原点
返回目录
(3)若Ax0+By0+C>0,则包含点P的半平面为不等式
所表示的平面区域,不包含点P的半平面为不等式 所表示的平面区域.
2.线性规划的有关概念
(1)线性约束条件——由条件列出一次不等式(或方程)组.
(2)线性目标函数——由条件列出一次函数表达式.
(3)线性规划问题:求线性目标函数在约束条件下的最大值或最小值问题.
Ax+By+C>0
Ax+By+C<0
返回目录
(4)可行解:满足 的解(x,y).
(5)可行域:所有 的集合.
(6)最优解:使 取得最大值或最小 值的可行解.
3.利用线性规划求最值,一般用图解法求解,其步骤是
(1)在平面直角坐标系内作出可行域.
(2)作出目标函数的等值线.
(3)确定最优解:在可行域内平行移动目标函数等值线,从而确定 .
(4)求最值:将最优解代入目标函数即可求出最大值或最小值.
最优解
线性约束条件
可行解
目标函数
返回目录
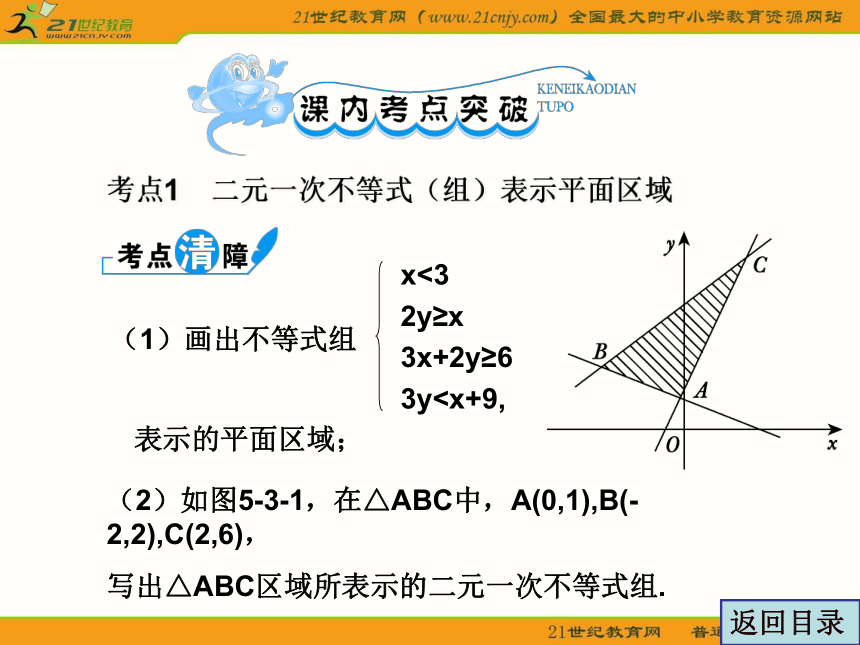
考点1 二元一次不等式(组)表示平面区域
x<3
2y≥x
3x+2y≥6
3y(2)如图5-3-1,在△ABC中,A(0,1),B(-2,2),C(2,6),
写出△ABC区域所表示的二元一次不等式组.
(1)画出不等式组
表示的平面区域;
返回目录
【分析】(1)分别画出每个不等式所表示的平面区域,然后取其公共部分.
(2)先由两点式分别求出直线AB,AC,BC的方程,然后写出不等式组.
【解析】(1)不等式x<3表示x=3左侧点的焦合.
不等式2y≥x表示x-2y=0上及其左上方点的集合.
不等式3x+2y≥6表示直线3x+2y-6=0
上及右上方点的集合.
不等式3y右下方的集合.
综上可得:不等式组表示的平面区域如图所示.
返回目录
(2)由两点式得直线AB,BC,CA的方程并化简为:
直线AB:x+2y-2=0,直线BC:x-y+4=0,直线CA:5x-2y+2=0.
∴原点(0,0)不在各直线上,将原点坐标代入到各直线方程左端,结合式子的符号可得不等式组为
x+2y-2≥0
x-y+4≥0
5x-2y+2≤0.
返回目录
二元一次不等式(组)表示平面区域的判断方法:
(1)直线定界,特殊点定域
注意不等式中有无等号,无等号时直线画成虚线,有等号时直线画成实线.若直线不过原点,特殊点常选取原点;若直线过原点,则特殊点常选取(1,0)或(0,1)来验证.
(2)同号上,异号下
即当B(Ax+By+C)>0时,区域为直线Ax+By+C=0的上方,当B(Ax+By+C)<0时,区域为直线Ax+By+C=0的下方.
返回目录
设集合A={(x,y)|x,y,1-x-y是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是( )
返回目录
返回目录
A(由于x,y,1-x-y是三角形的三边长,
x+y>1-x-y x+y> ,
x+1-x-y>y x< ,
y+1-x-y>x? y< .
再分别在同一坐标系中作直线x= ,y= ,
x+y= ,易知A正确.
故应选A.)
故有
返回目录
考点2 字母范围问题
x+y-11≥0
3x-y+3≥0
5x-3y+9≤0,
表示的平面区域为D.若指数函数y=ax的图象上存在区域D上的点,则a的取值范围是( )
A.(1,3] B.[2,3] C.(1,2] D.[3,+∞)
[2010年高考北京卷]设不等式组
【分析】作出平面区域D,对不同的a,研究什么时候满足条件,结合选项求a.
返回目录
【解析】作出不等式组表示的平面区域D,如图阴影部分所示.
x+y-11=0
3x-y+3=0
对y=ax的图象,当0没有点在区域D上.
当a>1,y=ax恰好经过A点时,由a2=9,得a=3.
要满足题意,需满足a2≤9,解得1故应选A.
由
得交点A(2,9).
返回目录
线性规划中的字母范围问题,要注意研究可行域以及字母与可行域联系.
返回目录
x-y+5≥0
y≥a
0≤x≤2
表示的平面区域是一个三角形,则a的取值范围是( )
A.a<5 B.a≥7
C.5≤a<7 D.a<5或a≥7
若不等式组
返回目录
【解析】如图,不等式组
x-y+5≥0
0≤x≤2
表示的平面区域与x轴构成一个
梯形,它的一个顶点坐标是(2,7)
用平行于x轴的直线y=a截梯形得到
三角形,则a的取值范围是5≤a<7.
故应选C.
返回目录
考点3 简单线性规划问题
[2010年高考山东卷]设变量x,y满足约束条件
x-y+2≥0
x-5y+10≤0
x+y-8≤0,
则目标函数z=3x-4y的最大值和最小值分别为( )
A.3,-11 B.-3,-11
C.11,-3 D.11,3
返回目录
【分析】画出不等式表示的可行域,由基本步骤求
目标函数的最大(小)值.
【解析】作出可行域如图阴影部
分所示,由图可知z=3x-4y经过点A时
z有最小值,经过点B时z有最大值.易
求A(3,5),B(5,3).
∴z最大=3×5-4×3=3,z最小=3×3-4×5=-11.
返回目录
线性规划求最值问题,要充分理解目标函数的几何意义,诸如直线的截距、两点间的距离(或平方)、点到直线的距离、过已知直线两点的斜率等.
返回目录
[2010年高考全国卷Ⅱ]若变量x,y满足约束条件
x≥-1
y≥x
3x+2y≤5,
A.1 B.2 C.3 D.4
名师伴你行
则z=2x+y的最大值为( )
返回目录
【解析】如图所示,由约束条件作出可行域.
将目标函数z=2x+y化为y=-2x+z,由图知在A点z取最大值.
y=x
3x+2y=5
∴zmax=2×1+1=3.
故应选C.
联立
得A(1,1).
返回目录
[2010年高考四川卷]某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
考点4 线性规划的应用
返回目录
【分析】将实际问题转化为线性规划问题,关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解.
【解析】设甲车间加工原料x箱,乙车间加工原料y
箱,由题意可知
x+y≤70
10x+6y≤480
x≥0
y≥0,
返回目录
甲、乙两车间每天总获利为z=280x+200y.
画出可行域如图所示.
点M(15,55)为直线x+y=70
和直线10x+6y=480的交点,
由图象知在点M(15,55)处z
取得最大值.
故应选B.
返回目录
(1)解决线性规划实际应用题的一般步骤:
①认真审题,分析并掌握实际问题的背景,设出未知数,写出线性约束条件和目标函数.
②作出可行域.
③作出目标函数值为零时对应的直线l.
④在可行域内平行移动直线l,从图中能判定问题有唯一最优解,或是有无穷最优解或无最优解.
⑤求出最优解,从而得到目标函数的最值.
返回目录
(2)解线性规划问题的关键步骤是在图上完成的,所以作图应尽可能精确,图上操作尽可能规范,假若图上的最优点并不明显时,不妨将几个有可能是最优点的坐标都求出来,然后逐一检验,以“验明正身”.另外对最优整数解问题,可使用“局部微调法”,其步骤可用以下十二字概括:微调整、求交点、取范围、找整解.
返回目录
[2010年高考陕西卷]铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为(百万元).
a b/万吨 c/百万元
A 50% 1 3
B 70% 0.5 6
返回目录
【解析】设购买A,B两种铁矿石分别为x万吨,y万吨,购买铁矿石的费用为z百万元,则z=3x+6y.
由题意可得约束条件为
x+ y≥1.9
x+ y≤2
x≥0
y≥0.
作出可行域如图所示,由图可知,目标函数z=3x+6y在点A(1,2)处取得最小值,zmin=3×1+6×2=15.
返回目录
1.判断二元一次不等式(组)表示平面区域的方法
(1)直线定界,特殊点定域
注意不等式中不等号有无等号,无等号时直线画成虚线,有等号时直线画成实线.若直线不过原点,特殊点常选取原点.
(2)同号上,异号下
即当B(Ax+By+C)>0时,区域为直线Ax+By+C=0的上方,当B(Ax+By+C)<0时,区域为直线Ax+By+C=0的下方.
返回目录
2.最优解的确定方法
线性目标函数z=ax+by取最大值时的最优解与b的正负有关,当b>0时,最优解是将直线ax+by=0的可行域内向上方平移到端点(一般是两直线交点)的位置得到的;当b<0时,则是向下方平移.
3.求线性规划问题时注意问题
用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.
返回目录
学案3 二元一次不等式(组)与简单
的线性规划问题
考点1
考点2
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
考点3
考点4
返回目录
考 纲 解 读
二元一次不等式(组)与简单的线性规划问题 1.能从实际问题中抽象出二元一次不等式组.
2.理解二元一次不等式组表示平面的区域,能够准确地画出可行域.
3.能够将实际问题抽象概括为线性规划问题,培养应用线性规划的知识解决实际问题的能力.
4.培养学生运用数学知识解决实际问题的能力,体会数形结合的数学思想.
考 向 预 测
从近几年的高考试题看,高考中常常以选择题、填空题的形式考查二元一次不等式组表示的平面区域的图形形状以及目标函数的最大值或最小值,有时也在解答题中考查线性规划、求函数的最优解等问题.已知目标函数的最值,求约束条件或目标函数中参数的取值问题,是高考的一种考查方向.
返回目录
1.二元一次不等式(组)表示平面区域
作二元一次不等式Ax+By+C>0(或Ax+By+C<0)表示的平面区域的方法步骤:
(1)在平面直角坐标系中作出直线Ax+By+C=0.
(2)在直线的一侧任取一点P(x0,y0),特别地,当C≠0时,常把 作为此特殊点.
原点
返回目录
(3)若Ax0+By0+C>0,则包含点P的半平面为不等式
所表示的平面区域,不包含点P的半平面为不等式 所表示的平面区域.
2.线性规划的有关概念
(1)线性约束条件——由条件列出一次不等式(或方程)组.
(2)线性目标函数——由条件列出一次函数表达式.
(3)线性规划问题:求线性目标函数在约束条件下的最大值或最小值问题.
Ax+By+C>0
Ax+By+C<0
返回目录
(4)可行解:满足 的解(x,y).
(5)可行域:所有 的集合.
(6)最优解:使 取得最大值或最小 值的可行解.
3.利用线性规划求最值,一般用图解法求解,其步骤是
(1)在平面直角坐标系内作出可行域.
(2)作出目标函数的等值线.
(3)确定最优解:在可行域内平行移动目标函数等值线,从而确定 .
(4)求最值:将最优解代入目标函数即可求出最大值或最小值.
最优解
线性约束条件
可行解
目标函数
返回目录
考点1 二元一次不等式(组)表示平面区域
x<3
2y≥x
3x+2y≥6
3y
写出△ABC区域所表示的二元一次不等式组.
(1)画出不等式组
表示的平面区域;
返回目录
【分析】(1)分别画出每个不等式所表示的平面区域,然后取其公共部分.
(2)先由两点式分别求出直线AB,AC,BC的方程,然后写出不等式组.
【解析】(1)不等式x<3表示x=3左侧点的焦合.
不等式2y≥x表示x-2y=0上及其左上方点的集合.
不等式3x+2y≥6表示直线3x+2y-6=0
上及右上方点的集合.
不等式3y
综上可得:不等式组表示的平面区域如图所示.
返回目录
(2)由两点式得直线AB,BC,CA的方程并化简为:
直线AB:x+2y-2=0,直线BC:x-y+4=0,直线CA:5x-2y+2=0.
∴原点(0,0)不在各直线上,将原点坐标代入到各直线方程左端,结合式子的符号可得不等式组为
x+2y-2≥0
x-y+4≥0
5x-2y+2≤0.
返回目录
二元一次不等式(组)表示平面区域的判断方法:
(1)直线定界,特殊点定域
注意不等式中有无等号,无等号时直线画成虚线,有等号时直线画成实线.若直线不过原点,特殊点常选取原点;若直线过原点,则特殊点常选取(1,0)或(0,1)来验证.
(2)同号上,异号下
即当B(Ax+By+C)>0时,区域为直线Ax+By+C=0的上方,当B(Ax+By+C)<0时,区域为直线Ax+By+C=0的下方.
返回目录
设集合A={(x,y)|x,y,1-x-y是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是( )
返回目录
返回目录
A(由于x,y,1-x-y是三角形的三边长,
x+y>1-x-y x+y> ,
x+1-x-y>y x< ,
y+1-x-y>x? y< .
再分别在同一坐标系中作直线x= ,y= ,
x+y= ,易知A正确.
故应选A.)
故有
返回目录
考点2 字母范围问题
x+y-11≥0
3x-y+3≥0
5x-3y+9≤0,
表示的平面区域为D.若指数函数y=ax的图象上存在区域D上的点,则a的取值范围是( )
A.(1,3] B.[2,3] C.(1,2] D.[3,+∞)
[2010年高考北京卷]设不等式组
【分析】作出平面区域D,对不同的a,研究什么时候满足条件,结合选项求a.
返回目录
【解析】作出不等式组表示的平面区域D,如图阴影部分所示.
x+y-11=0
3x-y+3=0
对y=ax的图象,当0
当a>1,y=ax恰好经过A点时,由a2=9,得a=3.
要满足题意,需满足a2≤9,解得1
由
得交点A(2,9).
返回目录
线性规划中的字母范围问题,要注意研究可行域以及字母与可行域联系.
返回目录
x-y+5≥0
y≥a
0≤x≤2
表示的平面区域是一个三角形,则a的取值范围是( )
A.a<5 B.a≥7
C.5≤a<7 D.a<5或a≥7
若不等式组
返回目录
【解析】如图,不等式组
x-y+5≥0
0≤x≤2
表示的平面区域与x轴构成一个
梯形,它的一个顶点坐标是(2,7)
用平行于x轴的直线y=a截梯形得到
三角形,则a的取值范围是5≤a<7.
故应选C.
返回目录
考点3 简单线性规划问题
[2010年高考山东卷]设变量x,y满足约束条件
x-y+2≥0
x-5y+10≤0
x+y-8≤0,
则目标函数z=3x-4y的最大值和最小值分别为( )
A.3,-11 B.-3,-11
C.11,-3 D.11,3
返回目录
【分析】画出不等式表示的可行域,由基本步骤求
目标函数的最大(小)值.
【解析】作出可行域如图阴影部
分所示,由图可知z=3x-4y经过点A时
z有最小值,经过点B时z有最大值.易
求A(3,5),B(5,3).
∴z最大=3×5-4×3=3,z最小=3×3-4×5=-11.
返回目录
线性规划求最值问题,要充分理解目标函数的几何意义,诸如直线的截距、两点间的距离(或平方)、点到直线的距离、过已知直线两点的斜率等.
返回目录
[2010年高考全国卷Ⅱ]若变量x,y满足约束条件
x≥-1
y≥x
3x+2y≤5,
A.1 B.2 C.3 D.4
名师伴你行
则z=2x+y的最大值为( )
返回目录
【解析】如图所示,由约束条件作出可行域.
将目标函数z=2x+y化为y=-2x+z,由图知在A点z取最大值.
y=x
3x+2y=5
∴zmax=2×1+1=3.
故应选C.
联立
得A(1,1).
返回目录
[2010年高考四川卷]某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
考点4 线性规划的应用
返回目录
【分析】将实际问题转化为线性规划问题,关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解.
【解析】设甲车间加工原料x箱,乙车间加工原料y
箱,由题意可知
x+y≤70
10x+6y≤480
x≥0
y≥0,
返回目录
甲、乙两车间每天总获利为z=280x+200y.
画出可行域如图所示.
点M(15,55)为直线x+y=70
和直线10x+6y=480的交点,
由图象知在点M(15,55)处z
取得最大值.
故应选B.
返回目录
(1)解决线性规划实际应用题的一般步骤:
①认真审题,分析并掌握实际问题的背景,设出未知数,写出线性约束条件和目标函数.
②作出可行域.
③作出目标函数值为零时对应的直线l.
④在可行域内平行移动直线l,从图中能判定问题有唯一最优解,或是有无穷最优解或无最优解.
⑤求出最优解,从而得到目标函数的最值.
返回目录
(2)解线性规划问题的关键步骤是在图上完成的,所以作图应尽可能精确,图上操作尽可能规范,假若图上的最优点并不明显时,不妨将几个有可能是最优点的坐标都求出来,然后逐一检验,以“验明正身”.另外对最优整数解问题,可使用“局部微调法”,其步骤可用以下十二字概括:微调整、求交点、取范围、找整解.
返回目录
[2010年高考陕西卷]铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为(百万元).
a b/万吨 c/百万元
A 50% 1 3
B 70% 0.5 6
返回目录
【解析】设购买A,B两种铁矿石分别为x万吨,y万吨,购买铁矿石的费用为z百万元,则z=3x+6y.
由题意可得约束条件为
x+ y≥1.9
x+ y≤2
x≥0
y≥0.
作出可行域如图所示,由图可知,目标函数z=3x+6y在点A(1,2)处取得最小值,zmin=3×1+6×2=15.
返回目录
1.判断二元一次不等式(组)表示平面区域的方法
(1)直线定界,特殊点定域
注意不等式中不等号有无等号,无等号时直线画成虚线,有等号时直线画成实线.若直线不过原点,特殊点常选取原点.
(2)同号上,异号下
即当B(Ax+By+C)>0时,区域为直线Ax+By+C=0的上方,当B(Ax+By+C)<0时,区域为直线Ax+By+C=0的下方.
返回目录
2.最优解的确定方法
线性目标函数z=ax+by取最大值时的最优解与b的正负有关,当b>0时,最优解是将直线ax+by=0的可行域内向上方平移到端点(一般是两直线交点)的位置得到的;当b<0时,则是向下方平移.
3.求线性规划问题时注意问题
用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.
返回目录
