2012届新课标高考数学文科一轮复习精选课件:2.11导数及其运算
文档属性
| 名称 | 2012届新课标高考数学文科一轮复习精选课件:2.11导数及其运算 |

|
|
| 格式 | rar | ||
| 文件大小 | 766.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
学案11 导数及其运算
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
知识网络构建
返回目录
考 纲 解 读
导数及其运算 (1)了解导数概念的实际背景.
(2)通过函数图象直观理解导数的几何意义.
(3)能根据导数的定义求函数y=C(C为常数),y=x,y= ,y=x2,y=x3,y=x的导数.
(4)能利用以下给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.
常见的基本初等函数的导数公式:
(C)′=0(C为常数);(xn)′=nxn-1(n∈N+);
(sinx)′=cosx;(cosx)′=-sinx;(ex)′=ex;(ax)′=axlna(a>0,且a≠1);
(lnx)′= ;(logax)′= logae(a>0,且a≠1).
常用的导数运算法则:
法则1:[u(x)±v(x)]′=u′(x)±v′(x).
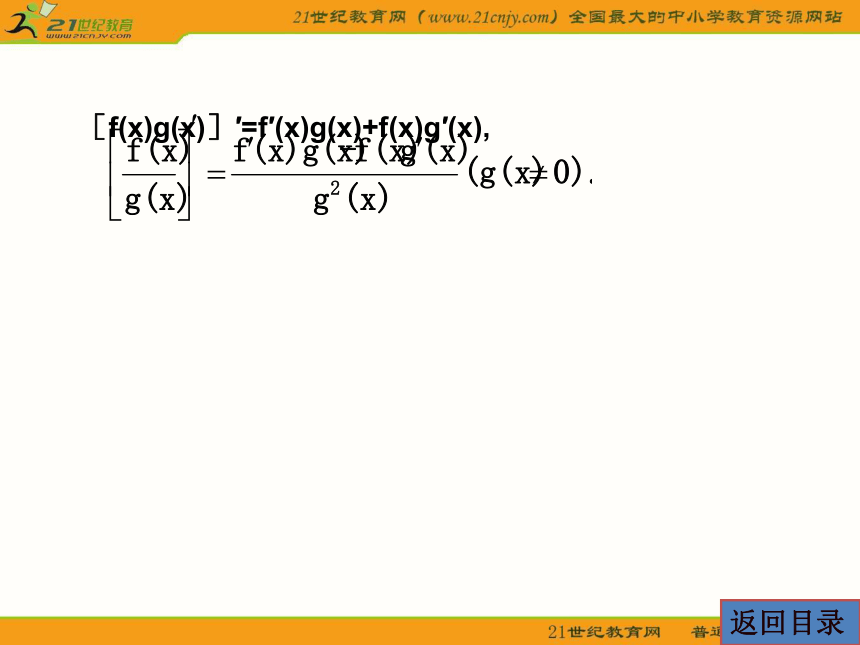
法则2:[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x).
法则3: (v(x)≠0).
考 向 预 测
1.导数的几何意义是高考考查的重点内容,常以选择题、填空题的形式出现,有时也出现在解答题中.
2.导数的运算每年必考,一般不单独考查,在考查导数应用的同时考查导数的运算.
返回目录
1.导数的概念
若函数y=f(x)在x0处的增量Δy与自变量的增量Δx的比值,当Δx→0时的极限lim = 存在,则称f(x)在x0处可导,并称此极限值为函数f(x)在x0处的导数,记为 或 .
Δx→0
y′|x=x
f′(x0)
0
返回目录
2.导函数
如果函数y=f(x)在开区间(a,b)内每一点都可导,就 说f(x)在区间(a,b)内可导,其导数也是开区间(a,b)内的函数,又称作f(x)的导函数,记作 或 .
3.函数f(x)在x0处的导数
函数f(x)的导函数f′(x)在x=x0处的函数值 即为函数f(x)在x0处的导数.
4.导数的几何意义
(1)设函数f(x)在x0处可导,则它在该点的导数等于函数所表示的曲线在相应点M(x0,y0)处的 .
(2)设s=s(t)是位移函数,则s′(t0)表示物体在t=t0时刻的 .
f′(x)
y′
f′(x0)
切线的斜率
瞬时速度
返回目录
(3)设v=v(t)是速度函数,则v′(t0)表示物体在t=t0时刻的 .
5.常用的导数公式
C′= (C为常数);(xm)′= (m∈Q);
(sinx)′= ;(cosx)′= ;
(ex)′= ;(ax)′= ;
(lnx)′= ;(logax)′= .
6.导数的运算法则
[f(x)±g(x)]′=f′(x)±g′(x),
[Cf(x)]′=Cf′(x)(C为常数),
加速度
0
mxm-1
cos x
-sinx
ex
axlna
logae
返回目录
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),
返回目录
返回目录
考点1 导数的定义
用定义法求下列函数的导数.
(1)y=x2; (2)y= .
【分析】先求 ,再求其Δx→0时的极限.
返回目录
【解析】 (1)∵
= =
=2x+Δx,
∴y′=lim =lim(2x+Δx)=2x.
(2)Δy= =- ,
=-4· ,
∴lim =lim [-4· ]= .
Δx→0
Δx→0
Δx→0
Δx→0
返回目录
利用导数定义求函数的导数应分三步:①求函数增量Δy;②求平均变化率 ;③求极限lim .
Δx→0
返回目录
用定义求函数y=f(x)= 在x=1处的导数.
返回目录
【解析】Δy=f(1+Δx)-f(1)
返回目录
考点2 求简单函数的导数
求下列各函数的导数:
返回目录
【分析】利用常见函数的导数及求导法则.
【 解析】(1)
返回目录
(2)当x>0时,y=lnx, y′= ;
当x<0时,y=ln(-x),
y′=( )·(-1)= .
∴y′= .
返回目录
(3)
(4) y′=(3xex)′-(2x)′+(e)′
=(3x)′ex+3x(ex)′-(2x)′+0
=3xln3·ex+3xex-2xln2
=(3e)xln3e-2xln2.
(5) y′=
=
= .
(6) y′=(xcosx)′-(sinx)′
=cosx-xsinx-cosx=-xsinx
返回目录
熟练运用导数的运算法则及复合函数的求导法则,并进行简单的求导数运算,注意运算中公式使用的合理性及准确性.
返回目录
(1)y=x2sinx;
(2)y= .
【解析】(1)y′=(x2)′sinx+x2(sinx)′
=2xsinx+x2cosx.
(2)y′=
=
= .
返回目录
考点3 导数的几何意义
[2009年高考江西卷]设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.4 B. C.2 D.
返回目录
【分析】利用导数的几何意义解题.
【解析】由条件知g′(1)=2,又∵f′(x)=[g(x)+x2]′=g′(x)+2x,∴f′(1)=g′(1)+2=2+2=4.
故应选A.
返回目录
曲线在某点处切线的斜率即为该点处的导数.
返回目录
已知曲线C:y=x3-3x2+2x,直线l:y=kx,且l与C切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
返回目录
∵直线l过原点,则k= (x0≠0).
由点(x0,y0)在曲线C上,
得y0= -3 +2x0,∴ = -3x0+2.
∵y′=3x2-6x+2,∴k=3 -6x0+2.
又k= ,∴2 -6x0+2= = -3x0+2,
整理得2 -3x0=0.
∵x0≠0,∴x0= ,
此时y0=- ,k=- ,
因此直线l的方程为y=- x,
切点坐标为( ,- ).
返回目录
1.在对导数的概念进行理解时,特别要注意f′(x0)与(f(x0))′是不一样的,f′(x0)代表函数f(x)在x=x0处的导数值,不一定为0;而(f(x0))′是函数值f(x0)的导数,而数值f(x0)是一个常量,其导数一定为0,即(f(x0))′=0.
2.对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.
返回目录
学案11 导数及其运算
考点1
考点2
考点3
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
知识网络构建
返回目录
考 纲 解 读
导数及其运算 (1)了解导数概念的实际背景.
(2)通过函数图象直观理解导数的几何意义.
(3)能根据导数的定义求函数y=C(C为常数),y=x,y= ,y=x2,y=x3,y=x的导数.
(4)能利用以下给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.
常见的基本初等函数的导数公式:
(C)′=0(C为常数);(xn)′=nxn-1(n∈N+);
(sinx)′=cosx;(cosx)′=-sinx;(ex)′=ex;(ax)′=axlna(a>0,且a≠1);
(lnx)′= ;(logax)′= logae(a>0,且a≠1).
常用的导数运算法则:
法则1:[u(x)±v(x)]′=u′(x)±v′(x).
法则2:[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x).
法则3: (v(x)≠0).
考 向 预 测
1.导数的几何意义是高考考查的重点内容,常以选择题、填空题的形式出现,有时也出现在解答题中.
2.导数的运算每年必考,一般不单独考查,在考查导数应用的同时考查导数的运算.
返回目录
1.导数的概念
若函数y=f(x)在x0处的增量Δy与自变量的增量Δx的比值,当Δx→0时的极限lim = 存在,则称f(x)在x0处可导,并称此极限值为函数f(x)在x0处的导数,记为 或 .
Δx→0
y′|x=x
f′(x0)
0
返回目录
2.导函数
如果函数y=f(x)在开区间(a,b)内每一点都可导,就 说f(x)在区间(a,b)内可导,其导数也是开区间(a,b)内的函数,又称作f(x)的导函数,记作 或 .
3.函数f(x)在x0处的导数
函数f(x)的导函数f′(x)在x=x0处的函数值 即为函数f(x)在x0处的导数.
4.导数的几何意义
(1)设函数f(x)在x0处可导,则它在该点的导数等于函数所表示的曲线在相应点M(x0,y0)处的 .
(2)设s=s(t)是位移函数,则s′(t0)表示物体在t=t0时刻的 .
f′(x)
y′
f′(x0)
切线的斜率
瞬时速度
返回目录
(3)设v=v(t)是速度函数,则v′(t0)表示物体在t=t0时刻的 .
5.常用的导数公式
C′= (C为常数);(xm)′= (m∈Q);
(sinx)′= ;(cosx)′= ;
(ex)′= ;(ax)′= ;
(lnx)′= ;(logax)′= .
6.导数的运算法则
[f(x)±g(x)]′=f′(x)±g′(x),
[Cf(x)]′=Cf′(x)(C为常数),
加速度
0
mxm-1
cos x
-sinx
ex
axlna
logae
返回目录
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),
返回目录
返回目录
考点1 导数的定义
用定义法求下列函数的导数.
(1)y=x2; (2)y= .
【分析】先求 ,再求其Δx→0时的极限.
返回目录
【解析】 (1)∵
= =
=2x+Δx,
∴y′=lim =lim(2x+Δx)=2x.
(2)Δy= =- ,
=-4· ,
∴lim =lim [-4· ]= .
Δx→0
Δx→0
Δx→0
Δx→0
返回目录
利用导数定义求函数的导数应分三步:①求函数增量Δy;②求平均变化率 ;③求极限lim .
Δx→0
返回目录
用定义求函数y=f(x)= 在x=1处的导数.
返回目录
【解析】Δy=f(1+Δx)-f(1)
返回目录
考点2 求简单函数的导数
求下列各函数的导数:
返回目录
【分析】利用常见函数的导数及求导法则.
【 解析】(1)
返回目录
(2)当x>0时,y=lnx, y′= ;
当x<0时,y=ln(-x),
y′=( )·(-1)= .
∴y′= .
返回目录
(3)
(4) y′=(3xex)′-(2x)′+(e)′
=(3x)′ex+3x(ex)′-(2x)′+0
=3xln3·ex+3xex-2xln2
=(3e)xln3e-2xln2.
(5) y′=
=
= .
(6) y′=(xcosx)′-(sinx)′
=cosx-xsinx-cosx=-xsinx
返回目录
熟练运用导数的运算法则及复合函数的求导法则,并进行简单的求导数运算,注意运算中公式使用的合理性及准确性.
返回目录
(1)y=x2sinx;
(2)y= .
【解析】(1)y′=(x2)′sinx+x2(sinx)′
=2xsinx+x2cosx.
(2)y′=
=
= .
返回目录
考点3 导数的几何意义
[2009年高考江西卷]设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.4 B. C.2 D.
返回目录
【分析】利用导数的几何意义解题.
【解析】由条件知g′(1)=2,又∵f′(x)=[g(x)+x2]′=g′(x)+2x,∴f′(1)=g′(1)+2=2+2=4.
故应选A.
返回目录
曲线在某点处切线的斜率即为该点处的导数.
返回目录
已知曲线C:y=x3-3x2+2x,直线l:y=kx,且l与C切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
返回目录
∵直线l过原点,则k= (x0≠0).
由点(x0,y0)在曲线C上,
得y0= -3 +2x0,∴ = -3x0+2.
∵y′=3x2-6x+2,∴k=3 -6x0+2.
又k= ,∴2 -6x0+2= = -3x0+2,
整理得2 -3x0=0.
∵x0≠0,∴x0= ,
此时y0=- ,k=- ,
因此直线l的方程为y=- x,
切点坐标为( ,- ).
返回目录
1.在对导数的概念进行理解时,特别要注意f′(x0)与(f(x0))′是不一样的,f′(x0)代表函数f(x)在x=x0处的导数值,不一定为0;而(f(x0))′是函数值f(x0)的导数,而数值f(x0)是一个常量,其导数一定为0,即(f(x0))′=0.
2.对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.
返回目录
