2012届高考数学文科一轮复习精选课件(新人教a版):6.1 数列
文档属性
| 名称 | 2012届高考数学文科一轮复习精选课件(新人教a版):6.1 数列 |
|
|
| 格式 | rar | ||
| 文件大小 | 820.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-15 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
学案1 数 列
考点1
考点2
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
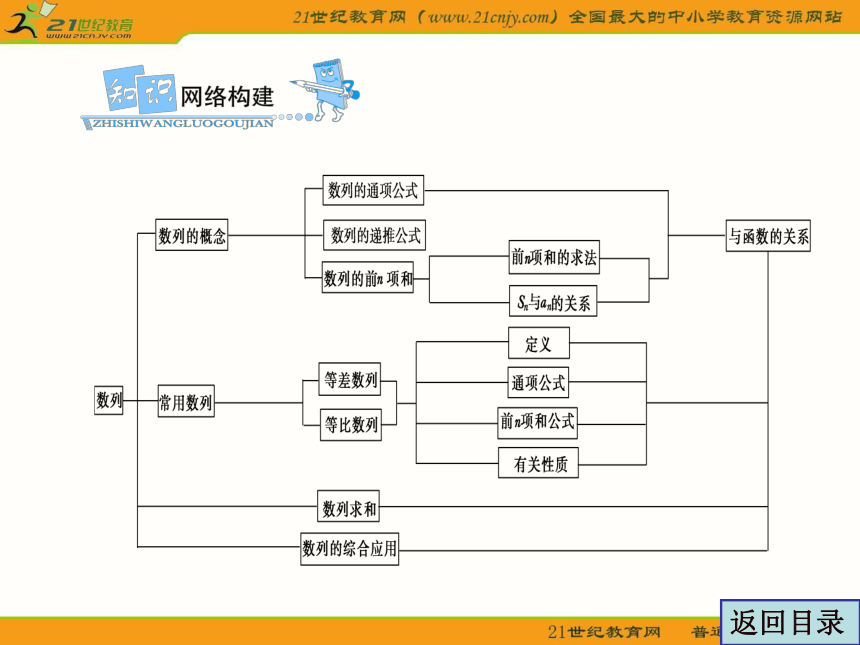
知识网络构建
返回目录
考 纲 解 读
数列 了解数列的概念和几种简单的表示方法.
了解数列是自变量为正整数的一类函数.
返回目录
从近两年的高考题来看,Sn与an的关系,数列的递推公式是高考的热点,题型为解答题,分值在12分左右,属较难题目,旨在考查学生分析问题、解决问题的能力.在考查基本知识的同时又注重考查等价转化、函数与方程、分类讨论等思想方法.
预测2012年高考仍将以Sn与an的关系为主要考点,重点考查学生的运算能力与逻辑推理能力.
考 向 预 测
返回目录
1.按照 叫做数列.数列中的 叫做这个数列的项;在函数意义下,数列是定义域为 的函数,f(n)是当自变量n从1开始依次取自然数时所对应的一列函数值f(1),f(2),…,f(n),….通常用an代替f(n),故数列的一般形式为:a1,a2,a3,…,an,…,简记为{an},其中an是数列的第 项.
一定次序排列着的一列数
每一个数
N* 或它的子集
n
返回目录
2.如果数列{an}的 与序号 之间的关系可以用一个式子an=f(n)来表示,那么 an= f(n)叫做数列的 .但并非每个数列都有通项公式,也并非都是唯一的.
3.如果已知数列{an}的第 项(或 ),且从第二项(或某一项)开始的 与它的 ( 或 )间的关系可以用一个公式来表示,那么这个公式叫数列的递推公式.数列常用的表示法有 :(通项公式或递推公式)、 、
.
第n项
n
通项公式
1
前几项
任一项an
前一项an-1
前几项
解析法
列表法
图象法
返回目录
4.数列按项数来分,分为 、 ;按项 增减规律分为 、 、 和 .
递增数列?an+1 an;递减数列?an+1 an;常数列?
an+1 an.递增数列与递减数列通称为 .
按任何一项的绝对值是否都小于某一正数来分,可分为 和 .
,(n=1)
,(n≥2).
an≥an-1, an≤an-1,
an≥an+1. an≤an+1.
Sn-Sn-1
5.已知Sn,则an=
数列{an}中,
若an最大,则
若an最小,则
有穷数列
无穷数列
递增数列
递减数列
摆动数列
常数列
>
<
=
单调数列
有界数列
无界数列
S1
返回目录
写出下面各数列的一个通项公式:
(1)3,5,7,9,…;
(2) …;
(3)-1, ,…;
考点1 由数列前几项求数列通项公式
返回目录
【分析】先观察各项的特点,然后归纳出其通项公式,要注意项与项数的关系及项与前后项的关系.
【解析】(1)各项减去1后为正偶数,
所以an=2n+1.
(2)每一项的分子比分母少1,而分母组成数列
21,22,23,24,…,所以an= .
(3)奇数项为负,偶数项为正,故通项公式中含因子(-1)n;各项绝对值的分母组成数列1,2,3,4,…;而各项绝对值的分子组成的数列中,奇数项为1,偶数项为3,即奇数项为2-1,偶数项为2+1,
返回目录
所以an=(-1)n· .
- (n为正奇数)
(n为正偶数).
也可写为an=
返回目录
(1)据所给数列的前几项求其通项公式时,需仔细观察分析,抓住以下几方面的特征:
①分式中分子、分母的特征;
②相邻项的变化特征;
③拆项后的特征;
④各项符号特征等,并对此进行归纳、联想.
(2)根据数列的前几项写出数列的一个通项公式是不完全归纳法蕴含着“从特殊到一般”的思想,由不完全归纳得出的结果是不可靠的,要注意代值检验,对于正负符号变化,可用(-1)n或(-1)n+1来调整.
返回目录
根据数列的前几项,写出下列各数列的一个通项公式:
(1) , , , ,…;
(2)1,3,6,10,15,…;
(3) , ,- , ,…;
(4)7,77,777,….
返回目录
(1) 注意前四项中有两项的分子均为4,不妨把分子都统一为4,即: , , , ,….因而有an= .
(2)注意6=2×3,10=2×5,15=3×5,规律还不明显,再把各项同乘以2再除以2,即
,…,因而有an= .
返回目录
(3)其分母的规律是明显的,关键在于观察分子,分子后三项绝对值递增,且比分母小3.又注意到第三项为
负,而第一项的分子也可以写成-(-1),∴an=(-1)n .
(4)把各项除以7,得1,11,111,…,再乘以9,
得9,99,999,….∴an= (10n-1).
返回目录
考点2 公式法求通项公式
直接求通
【分析】由公式
S1 n=1
Sn-Sn-1 n≥2
项公式.
an=
已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.
(1)Sn=2n2-3n;(2)Sn=3n-2;(3)Sn=3an-2.
返回目录
【解析】 (1)a1=S1=-1,当n≥2时,
an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5.
由于a1也适合此等式,因此an=4n-5(n∈N*).
(2)a1=S1=1,当n≥2时,
an=Sn-Sn-1=(3n-2)-(3n-1-2)=2·3n-1.
1 (n=1),
2·3n-1 (n≥2).
∴an=
返回目录
(3)∵an=Sn-Sn-1=(3an-2)-(3an-1-2),
∴an= an-1(n≥2).
又a1=S1=3a1-2,∴a1=1.
∴{an}是以1为首项, 为公比的等比数列.
∴an=1·( )n-1=( )n-1.
返回目录
数列的通项an与前n项和Sn的关系是
S1(n=1)
Sn-Sn-1(n≥2),
视.已知an求Sn时方法千差万别,但已知Sn求an时方法却是高度统一.当n≥2时求出an也适合n=1时的情形, 可直接写成an=Sn-Sn-1,否则分段表示.
此公式经常使用,应引起足够的重
an=
返回目录
已知数列{ an }的前n项和Sn满足an+2SnSn-1=0
(n≥2),a1= ,求an.
返回目录
∵当n≥2时,an=Sn-Sn-1,∴Sn-Sn-1+2SnSn-1=0,
即 =2,∴数列{ } 是公差为2的等差数列.
又S1=a1=12,∴ =2,
∴ =2+(n-1)·2=2n,∴Sn= .
∴当n≥2时,an=-2SnSn-1
=-2· · =- ,
(n=1)
(n≥2).
∴an=
返回目录
1.用归纳法据前几项写出数列的一个通项公式,体现了由特殊到一般的思维方法,需要我们有一定的数学观察能力和分析能力,并熟知一些常见的数列的通项公式,如:数列{n2},{2n},{(-1)n},{2n},{2n-1}.
2.对于符号(数字、字母、运算符号、关系符号)、图形、文字所表示的数学问题,要有目的的观察并得出结论,是学习数学应重视的能力,应多进行对比、分析,从整体到局部多角度进行观察.观察的结果要准确、完整、深刻.
返回目录
学案1 数 列
考点1
考点2
填填知学情
课内考点突破
规 律 探 究
考 纲 解 读
考 向 预 测
知识网络构建
返回目录
考 纲 解 读
数列 了解数列的概念和几种简单的表示方法.
了解数列是自变量为正整数的一类函数.
返回目录
从近两年的高考题来看,Sn与an的关系,数列的递推公式是高考的热点,题型为解答题,分值在12分左右,属较难题目,旨在考查学生分析问题、解决问题的能力.在考查基本知识的同时又注重考查等价转化、函数与方程、分类讨论等思想方法.
预测2012年高考仍将以Sn与an的关系为主要考点,重点考查学生的运算能力与逻辑推理能力.
考 向 预 测
返回目录
1.按照 叫做数列.数列中的 叫做这个数列的项;在函数意义下,数列是定义域为 的函数,f(n)是当自变量n从1开始依次取自然数时所对应的一列函数值f(1),f(2),…,f(n),….通常用an代替f(n),故数列的一般形式为:a1,a2,a3,…,an,…,简记为{an},其中an是数列的第 项.
一定次序排列着的一列数
每一个数
N* 或它的子集
n
返回目录
2.如果数列{an}的 与序号 之间的关系可以用一个式子an=f(n)来表示,那么 an= f(n)叫做数列的 .但并非每个数列都有通项公式,也并非都是唯一的.
3.如果已知数列{an}的第 项(或 ),且从第二项(或某一项)开始的 与它的 ( 或 )间的关系可以用一个公式来表示,那么这个公式叫数列的递推公式.数列常用的表示法有 :(通项公式或递推公式)、 、
.
第n项
n
通项公式
1
前几项
任一项an
前一项an-1
前几项
解析法
列表法
图象法
返回目录
4.数列按项数来分,分为 、 ;按项 增减规律分为 、 、 和 .
递增数列?an+1 an;递减数列?an+1 an;常数列?
an+1 an.递增数列与递减数列通称为 .
按任何一项的绝对值是否都小于某一正数来分,可分为 和 .
,(n=1)
,(n≥2).
an≥an-1, an≤an-1,
an≥an+1. an≤an+1.
Sn-Sn-1
5.已知Sn,则an=
数列{an}中,
若an最大,则
若an最小,则
有穷数列
无穷数列
递增数列
递减数列
摆动数列
常数列
>
<
=
单调数列
有界数列
无界数列
S1
返回目录
写出下面各数列的一个通项公式:
(1)3,5,7,9,…;
(2) …;
(3)-1, ,…;
考点1 由数列前几项求数列通项公式
返回目录
【分析】先观察各项的特点,然后归纳出其通项公式,要注意项与项数的关系及项与前后项的关系.
【解析】(1)各项减去1后为正偶数,
所以an=2n+1.
(2)每一项的分子比分母少1,而分母组成数列
21,22,23,24,…,所以an= .
(3)奇数项为负,偶数项为正,故通项公式中含因子(-1)n;各项绝对值的分母组成数列1,2,3,4,…;而各项绝对值的分子组成的数列中,奇数项为1,偶数项为3,即奇数项为2-1,偶数项为2+1,
返回目录
所以an=(-1)n· .
- (n为正奇数)
(n为正偶数).
也可写为an=
返回目录
(1)据所给数列的前几项求其通项公式时,需仔细观察分析,抓住以下几方面的特征:
①分式中分子、分母的特征;
②相邻项的变化特征;
③拆项后的特征;
④各项符号特征等,并对此进行归纳、联想.
(2)根据数列的前几项写出数列的一个通项公式是不完全归纳法蕴含着“从特殊到一般”的思想,由不完全归纳得出的结果是不可靠的,要注意代值检验,对于正负符号变化,可用(-1)n或(-1)n+1来调整.
返回目录
根据数列的前几项,写出下列各数列的一个通项公式:
(1) , , , ,…;
(2)1,3,6,10,15,…;
(3) , ,- , ,…;
(4)7,77,777,….
返回目录
(1) 注意前四项中有两项的分子均为4,不妨把分子都统一为4,即: , , , ,….因而有an= .
(2)注意6=2×3,10=2×5,15=3×5,规律还不明显,再把各项同乘以2再除以2,即
,…,因而有an= .
返回目录
(3)其分母的规律是明显的,关键在于观察分子,分子后三项绝对值递增,且比分母小3.又注意到第三项为
负,而第一项的分子也可以写成-(-1),∴an=(-1)n .
(4)把各项除以7,得1,11,111,…,再乘以9,
得9,99,999,….∴an= (10n-1).
返回目录
考点2 公式法求通项公式
直接求通
【分析】由公式
S1 n=1
Sn-Sn-1 n≥2
项公式.
an=
已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.
(1)Sn=2n2-3n;(2)Sn=3n-2;(3)Sn=3an-2.
返回目录
【解析】 (1)a1=S1=-1,当n≥2时,
an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5.
由于a1也适合此等式,因此an=4n-5(n∈N*).
(2)a1=S1=1,当n≥2时,
an=Sn-Sn-1=(3n-2)-(3n-1-2)=2·3n-1.
1 (n=1),
2·3n-1 (n≥2).
∴an=
返回目录
(3)∵an=Sn-Sn-1=(3an-2)-(3an-1-2),
∴an= an-1(n≥2).
又a1=S1=3a1-2,∴a1=1.
∴{an}是以1为首项, 为公比的等比数列.
∴an=1·( )n-1=( )n-1.
返回目录
数列的通项an与前n项和Sn的关系是
S1(n=1)
Sn-Sn-1(n≥2),
视.已知an求Sn时方法千差万别,但已知Sn求an时方法却是高度统一.当n≥2时求出an也适合n=1时的情形, 可直接写成an=Sn-Sn-1,否则分段表示.
此公式经常使用,应引起足够的重
an=
返回目录
已知数列{ an }的前n项和Sn满足an+2SnSn-1=0
(n≥2),a1= ,求an.
返回目录
∵当n≥2时,an=Sn-Sn-1,∴Sn-Sn-1+2SnSn-1=0,
即 =2,∴数列{ } 是公差为2的等差数列.
又S1=a1=12,∴ =2,
∴ =2+(n-1)·2=2n,∴Sn= .
∴当n≥2时,an=-2SnSn-1
=-2· · =- ,
(n=1)
(n≥2).
∴an=
返回目录
1.用归纳法据前几项写出数列的一个通项公式,体现了由特殊到一般的思维方法,需要我们有一定的数学观察能力和分析能力,并熟知一些常见的数列的通项公式,如:数列{n2},{2n},{(-1)n},{2n},{2n-1}.
2.对于符号(数字、字母、运算符号、关系符号)、图形、文字所表示的数学问题,要有目的的观察并得出结论,是学习数学应重视的能力,应多进行对比、分析,从整体到局部多角度进行观察.观察的结果要准确、完整、深刻.
返回目录
