2.3.2-2.3.3平面向量的正交分解及坐标表示和运算(共24张PPT)
文档属性
| 名称 | 2.3.2-2.3.3平面向量的正交分解及坐标表示和运算(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览





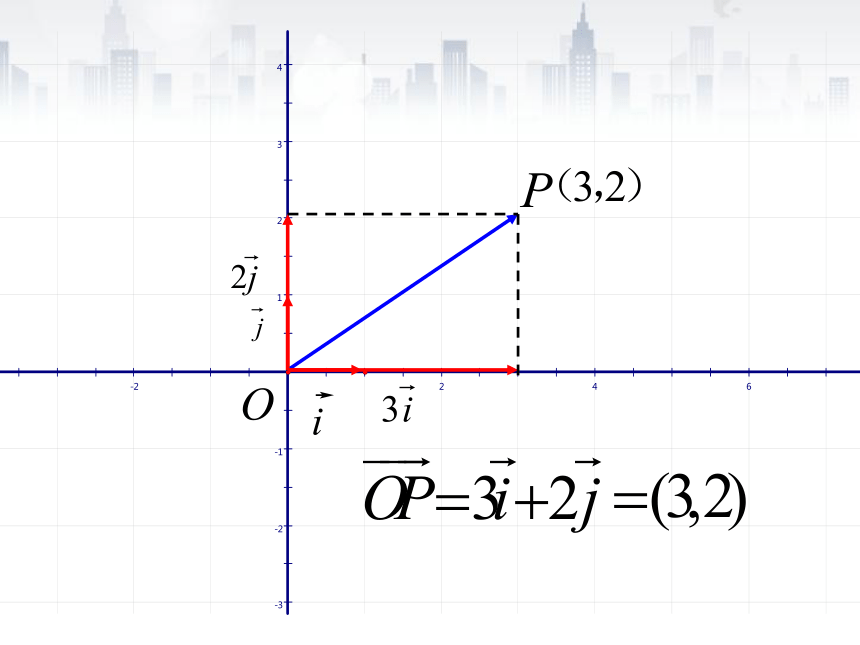
文档简介
(共24张PPT)
复习
平面向量基本定理:
复习
平面向量基本定理:
(2)基底不唯一,关键是不共线;
复习
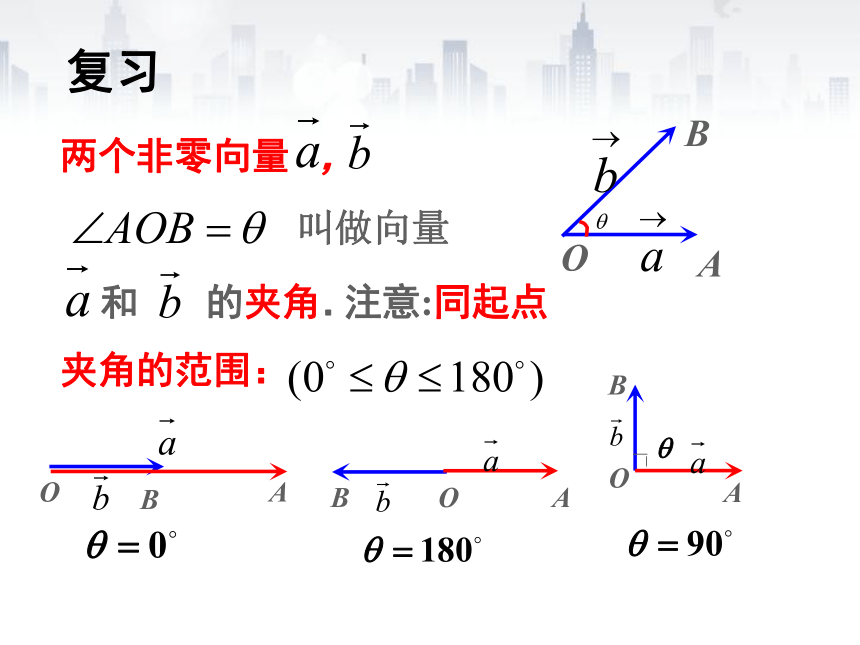
两个非零向量
,
和
的夹角.
夹角的范围:
注意:同起点
叫做向量
定义:把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
直角坐标系中,点A的
坐标(x
,y)的含义是什么?
OM=x,ON=y
思考:互相垂直的两个向量能否作为平面内所有向量的一组基底?
探索1:
以O为起点,
P
为终点的向量能否用坐标表示?如何表示?
向量的坐标表示
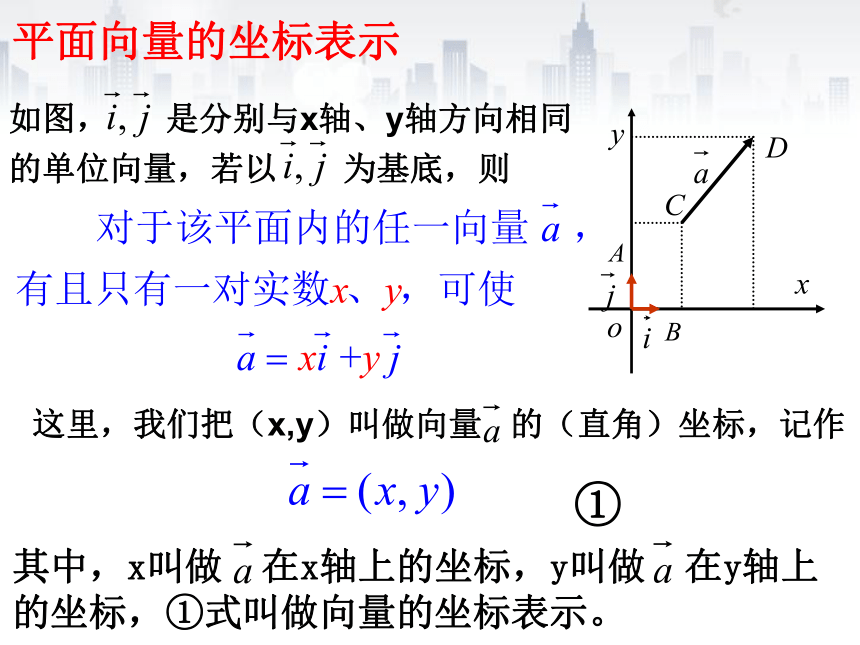
平面向量的坐标表示
①
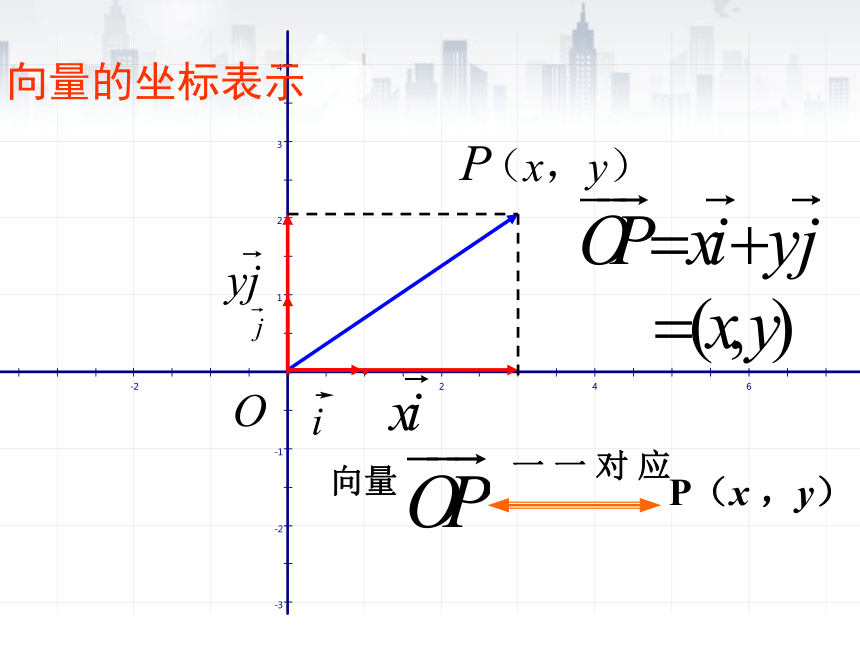
向量的坐标表示
O
x
y
A
当向量的起点在坐标原点时,向量的坐标就是向量终点的坐标.
两个向量相等,利用坐标如何表示?
2.已知
则下列说法正确的是( )
A.B点的坐标是(4,2)
B.A点的坐标是(4,2)
C.当A为原点时,B点的坐标是(4,2)
D.当B为原点时,A点的坐标是(4,2)
C
全优53页基础夯实
2.若向量(x,y)=0,则必有( )
A.x=0或y=0
B.x=0且y=0
C.xy=0
D.x+y=0
B
全优91页限时规范训练
例2.如图,分别用基底
、表示向量
、
、
、
,并求出
它们的坐标。
A
A1
A2
解:如图可知
同理
问题:
若已知
=(1
,3)
,
=(5
,1),
(6,4)
问题:
若已知
=(1
,3)
,
=(5
,1),
猜想:
=(x1
,
)
+
(
,
y2
)
平面向量的坐标运算法则
结论:两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差)。
向量的数乘运算
?
结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标
解:
=(6,3)+(-12,16)
=(-6,19).
课本
P
100
1
课本
P
100
2
5.已知a=(1,2),b=(-4,4),c=(-3,-6)且c=xa+yb(x,y∈R),则x+y=________.
-3
【解析】由c=xa+yb,得
(-3,-6)=x(1,2)+y(-4,4)
=(x-4y,2x+4y),
解得x=-3,y=0,
则x+y=-3.
全优53页基础夯实
x
y
O
B
A
一个向量的坐标等于表示此向量的有向
线段的终点的坐标减去起点的坐标.
解:
练习:课本100页3(1)(2)
例4 如图,已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)
、(3,4),试求顶点D的坐标.
解法1:设顶点D的坐标为(x,y).
(1,2)=(3-x,4-y)
.
∴顶点D的坐标为(2,2).
解法2:如图,由向量加法的平行四边形法则可知
∴顶点D的坐标为(2,2).
=(-2-(-1),1-3)+(3-(-1),4-3)
=(2,2).
=(3,-1),
例4 如图,已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)
、(3,4),试求顶点D的坐标.
复习
平面向量基本定理:
复习
平面向量基本定理:
(2)基底不唯一,关键是不共线;
复习
两个非零向量
,
和
的夹角.
夹角的范围:
注意:同起点
叫做向量
定义:把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
直角坐标系中,点A的
坐标(x
,y)的含义是什么?
OM=x,ON=y
思考:互相垂直的两个向量能否作为平面内所有向量的一组基底?
探索1:
以O为起点,
P
为终点的向量能否用坐标表示?如何表示?
向量的坐标表示
平面向量的坐标表示
①
向量的坐标表示
O
x
y
A
当向量的起点在坐标原点时,向量的坐标就是向量终点的坐标.
两个向量相等,利用坐标如何表示?
2.已知
则下列说法正确的是( )
A.B点的坐标是(4,2)
B.A点的坐标是(4,2)
C.当A为原点时,B点的坐标是(4,2)
D.当B为原点时,A点的坐标是(4,2)
C
全优53页基础夯实
2.若向量(x,y)=0,则必有( )
A.x=0或y=0
B.x=0且y=0
C.xy=0
D.x+y=0
B
全优91页限时规范训练
例2.如图,分别用基底
、表示向量
、
、
、
,并求出
它们的坐标。
A
A1
A2
解:如图可知
同理
问题:
若已知
=(1
,3)
,
=(5
,1),
(6,4)
问题:
若已知
=(1
,3)
,
=(5
,1),
猜想:
=(x1
,
)
+
(
,
y2
)
平面向量的坐标运算法则
结论:两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差)。
向量的数乘运算
?
结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标
解:
=(6,3)+(-12,16)
=(-6,19).
课本
P
100
1
课本
P
100
2
5.已知a=(1,2),b=(-4,4),c=(-3,-6)且c=xa+yb(x,y∈R),则x+y=________.
-3
【解析】由c=xa+yb,得
(-3,-6)=x(1,2)+y(-4,4)
=(x-4y,2x+4y),
解得x=-3,y=0,
则x+y=-3.
全优53页基础夯实
x
y
O
B
A
一个向量的坐标等于表示此向量的有向
线段的终点的坐标减去起点的坐标.
解:
练习:课本100页3(1)(2)
例4 如图,已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)
、(3,4),试求顶点D的坐标.
解法1:设顶点D的坐标为(x,y).
(1,2)=(3-x,4-y)
.
∴顶点D的坐标为(2,2).
解法2:如图,由向量加法的平行四边形法则可知
∴顶点D的坐标为(2,2).
=(-2-(-1),1-3)+(3-(-1),4-3)
=(2,2).
=(3,-1),
例4 如图,已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3)
、(3,4),试求顶点D的坐标.
