11.2.1 三角形的内角课时达标(含答案)
文档属性
| 名称 | 11.2.1 三角形的内角课时达标(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
11.2.1三角形的内角课时达标
一、选择题
1、已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60°
B.30°
C.20°
D.40°
2、在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.75°???
B.60°
??
C.45°?
??
D.30°?
3、如图,∠BAC=90°,AD⊥BC,则图中互余的角有(
??)
A.2对?
B.3对??
C.4对??
D.5对
4、一个三角形中,有一个角是55°,另外的两个角可能是(???????
)
A.
95°,20°???????????
B.
45°,80°?
C.
55°,60°???????????
D.
90°,20°
5、如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
A.95°
B.120°???
C.135°???
D.无法确定
6、三角形的一个外角等于与它不相邻的内角的4倍,等于与它相邻的一个内角的2倍,则这个三角形各角的度数为(
)
A.45°,45°,90°?
B.30°,60°,90°
C.25°,25°,130°
D.36°,72°,72°
7、直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为(
)
A.60°???????????
B.50°????????
C.40°????????
D.30°
8、等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为
A.45°???????????
B.135°???????
C.45°或67.5°
D.45°或135°
9、在下列条件中:①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°-∠B;④∠A=∠B=∠C.能确定△ABC是直角三角形的条件有
A.1个???????????
B.2个????????
C.3个????????
D.4个
二、填空题
10、在△ABC中,若∠B-∠A=15°,∠C-∠B=60°,则∠A=______,∠B=______,∠C=______.
11、一个人从A点出发向北偏东30°方向走到B点,再从B点出发向南偏东15°方向走到C点,此时C点正好在A点的北偏东70°的方向上,那么∠ACB的度数是__
12、图所示是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处∠BCD的度数为??
????.
13、.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是__________.
14、当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”。如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为___________度。
三、解答题
15、如图,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
16、已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
17、如图所示,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,∠BPC=134°,求∠A的度数.
???????????????????????????????????????????
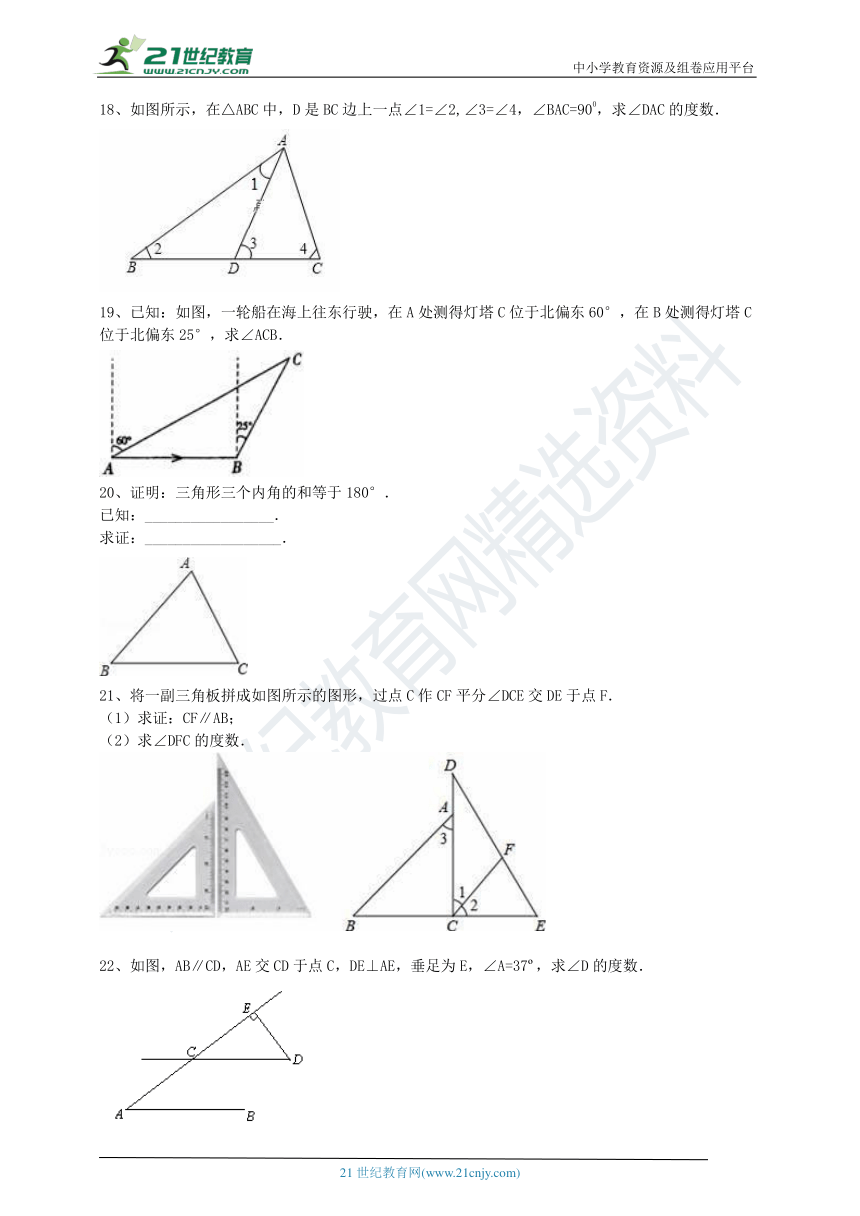
18、如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=900,求∠DAC的度数.
19、已知:如图,一轮船在海上往东行驶,在A处测得灯塔C位于北偏东60°,在B处测得灯塔C位于北偏东25°,求∠ACB.
20、证明:三角形三个内角的和等于180°.
已知:_________________.
求证:__________________.
21、将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
22、如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37?,求∠D的度数.
23、如图,三角形ABC中,DE∥AC,DF∥AB,试问∠A+∠B+∠C=180°这个结论成立吗?若成立,试写出推理过程;若不成立,请说明理由。OD平分∠COB。
(1)求∠DOC的度数;
(2)判断AB与OC的位置关系。
24、如图,在△ABC中,∠B<∠ACB,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD,且PE交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,求证:∠E=(∠ACB-∠B).
参考答案
一、选择题
1、D
2、D
?
3、C
4、B
5、C
6、B
7、C
8、D
9、C
二、填空题
10、30°,45°,105°.
11、95°__.
12、?119°
??.
13、α=β+γ.
【考点】三角形内角和定理.
【专题】探究型.
【分析】根据三角形的内角和是个定值180度计算.
【解答】解:∵三角内角和是个定值为180度,
∴∠A+∠B+∠C=180°
∴∠A越来越小,∠B、∠C越来越大时,
∴∠A﹣α+∠B+β+∠C+γ=180°,
∴α=β+γ.
故答案为:α=β+γ.
【点评】主要考查了三角形的内角和为180度这个知识点.
14、30
三、解答题
15、.解:设∠DAC=x,则∠BAD=57°-x.
∵∠C=∠ADC,
∴∠ADC=(180°-x).
又∵AD=BD,
∴∠B=∠BAD=57°-x.
∵∠ADC=∠B+∠BAD,
∴(180°-x)=2(57°-x),
解得x=16°.
即∠DAC的度数为16°.
16、解:∵在△ABC中,∠A:∠B:∠C=2:3:4,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°???????
∵CD是∠ACB平分线,
∴∠ACD=∠ACB=40°??????????????????????????
∴∠CDB=∠A+∠ACD=40°+40°=80°??????????????
18、32?,?
19、35°.
20、【考点】:三角形内角和定理.
【分析】画出画图,已知△ABC、求证:∠BAC+∠B+∠C=180°.过点A作EF∥BC,利用EF∥BC,可得∠1=∠B,∠2=∠C,而∠1+∠2+∠BAC=180°,利用等量代换可证∠BAC+∠B+∠C=180°.
【解答】解:已知:△ABC,
求证:∠BAC+∠B+∠C=180°,
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即知三角形内角和等于180°.
故答案为:△ABC;∠BAC+∠B+∠C=180°.
【点评】本题考查证明三角形内角和定理,解题的关键是做平行线,利用平行线的性质进行证明.
21、【考点】平行线的判定;角平分线的定义;三角形内角和定理.
【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;
(2)利用三角形内角和定理进行计算即可.
【解答】(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE,
∵∠DCE=90°,
∴∠1=45°,
∵∠3=45°,
∴∠1=∠3,
∴AB∥CF(内错角相等,两直线平行);
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
【点评】此题主要考查了平行线的判定,以及三角形内角和定理,关键是掌握内错角相等,两直线平行.
22、∵CD∥AB
∴∠A=∠ECD
∵∠A=37????
∴∠ECD=37?
∵DE⊥AE?
∴∠DEC=90?
∵∠ECD+∠DEC+∠D=180?
∴∠D=53?
23、成立。因为DE∥AC,所以∠C=∠EDB,∠EDF=∠DFC;又因为DF∥AB,所以∠B=∠FDC,∠A=∠DFC=∠EDF;即∠A+∠B+∠C=∠EDF+∠FDC+∠EDB,而∠EDF+∠FDC+∠EDB=180°,故∠A+∠B+∠C=180°。
24、(1)解:∵∠B=35°,∠ACB=85°,∴∠BAC=60°.
∵AD平分∠BAC,
∴∠DAC=30°.
∴∠ADC=65°.
又∵PE⊥AD,
∴∠DPE=90°.
∴∠E=25°.
(2)证明:∵∠B+∠BAC+∠ACB=180°,
∴∠BAC=180°-(∠B+∠ACB).
∵AD平分∠BAC,
∴∠BAD=∠BAC=90°-(∠B+∠ACB).
∴∠ADC=∠B+∠BAD=90°-(∠ACB-∠B).
∵PE⊥AD,
∴∠DPE=90°.
∴∠ADC+∠E=90°.
∴∠E=90°-∠ADC.
∴∠E=(∠ACB-∠B).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.2.1三角形的内角课时达标
一、选择题
1、已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
A.60°
B.30°
C.20°
D.40°
2、在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.75°???
B.60°
??
C.45°?
??
D.30°?
3、如图,∠BAC=90°,AD⊥BC,则图中互余的角有(
??)
A.2对?
B.3对??
C.4对??
D.5对
4、一个三角形中,有一个角是55°,另外的两个角可能是(???????
)
A.
95°,20°???????????
B.
45°,80°?
C.
55°,60°???????????
D.
90°,20°
5、如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
A.95°
B.120°???
C.135°???
D.无法确定
6、三角形的一个外角等于与它不相邻的内角的4倍,等于与它相邻的一个内角的2倍,则这个三角形各角的度数为(
)
A.45°,45°,90°?
B.30°,60°,90°
C.25°,25°,130°
D.36°,72°,72°
7、直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为(
)
A.60°???????????
B.50°????????
C.40°????????
D.30°
8、等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为
A.45°???????????
B.135°???????
C.45°或67.5°
D.45°或135°
9、在下列条件中:①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°-∠B;④∠A=∠B=∠C.能确定△ABC是直角三角形的条件有
A.1个???????????
B.2个????????
C.3个????????
D.4个
二、填空题
10、在△ABC中,若∠B-∠A=15°,∠C-∠B=60°,则∠A=______,∠B=______,∠C=______.
11、一个人从A点出发向北偏东30°方向走到B点,再从B点出发向南偏东15°方向走到C点,此时C点正好在A点的北偏东70°的方向上,那么∠ACB的度数是__
12、图所示是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处∠BCD的度数为??
????.
13、.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是__________.
14、当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”。如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为___________度。
三、解答题
15、如图,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
16、已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
17、如图所示,在△ABC中,BP、CP分别是∠ABC和∠ACB的角平分线,∠BPC=134°,求∠A的度数.
???????????????????????????????????????????
18、如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=900,求∠DAC的度数.
19、已知:如图,一轮船在海上往东行驶,在A处测得灯塔C位于北偏东60°,在B处测得灯塔C位于北偏东25°,求∠ACB.
20、证明:三角形三个内角的和等于180°.
已知:_________________.
求证:__________________.
21、将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
22、如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37?,求∠D的度数.
23、如图,三角形ABC中,DE∥AC,DF∥AB,试问∠A+∠B+∠C=180°这个结论成立吗?若成立,试写出推理过程;若不成立,请说明理由。OD平分∠COB。
(1)求∠DOC的度数;
(2)判断AB与OC的位置关系。
24、如图,在△ABC中,∠B<∠ACB,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD,且PE交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,求证:∠E=(∠ACB-∠B).
参考答案
一、选择题
1、D
2、D
?
3、C
4、B
5、C
6、B
7、C
8、D
9、C
二、填空题
10、30°,45°,105°.
11、95°__.
12、?119°
??.
13、α=β+γ.
【考点】三角形内角和定理.
【专题】探究型.
【分析】根据三角形的内角和是个定值180度计算.
【解答】解:∵三角内角和是个定值为180度,
∴∠A+∠B+∠C=180°
∴∠A越来越小,∠B、∠C越来越大时,
∴∠A﹣α+∠B+β+∠C+γ=180°,
∴α=β+γ.
故答案为:α=β+γ.
【点评】主要考查了三角形的内角和为180度这个知识点.
14、30
三、解答题
15、.解:设∠DAC=x,则∠BAD=57°-x.
∵∠C=∠ADC,
∴∠ADC=(180°-x).
又∵AD=BD,
∴∠B=∠BAD=57°-x.
∵∠ADC=∠B+∠BAD,
∴(180°-x)=2(57°-x),
解得x=16°.
即∠DAC的度数为16°.
16、解:∵在△ABC中,∠A:∠B:∠C=2:3:4,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°???????
∵CD是∠ACB平分线,
∴∠ACD=∠ACB=40°??????????????????????????
∴∠CDB=∠A+∠ACD=40°+40°=80°??????????????
18、32?,?
19、35°.
20、【考点】:三角形内角和定理.
【分析】画出画图,已知△ABC、求证:∠BAC+∠B+∠C=180°.过点A作EF∥BC,利用EF∥BC,可得∠1=∠B,∠2=∠C,而∠1+∠2+∠BAC=180°,利用等量代换可证∠BAC+∠B+∠C=180°.
【解答】解:已知:△ABC,
求证:∠BAC+∠B+∠C=180°,
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即知三角形内角和等于180°.
故答案为:△ABC;∠BAC+∠B+∠C=180°.
【点评】本题考查证明三角形内角和定理,解题的关键是做平行线,利用平行线的性质进行证明.
21、【考点】平行线的判定;角平分线的定义;三角形内角和定理.
【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;
(2)利用三角形内角和定理进行计算即可.
【解答】(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE,
∵∠DCE=90°,
∴∠1=45°,
∵∠3=45°,
∴∠1=∠3,
∴AB∥CF(内错角相等,两直线平行);
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
【点评】此题主要考查了平行线的判定,以及三角形内角和定理,关键是掌握内错角相等,两直线平行.
22、∵CD∥AB
∴∠A=∠ECD
∵∠A=37????
∴∠ECD=37?
∵DE⊥AE?
∴∠DEC=90?
∵∠ECD+∠DEC+∠D=180?
∴∠D=53?
23、成立。因为DE∥AC,所以∠C=∠EDB,∠EDF=∠DFC;又因为DF∥AB,所以∠B=∠FDC,∠A=∠DFC=∠EDF;即∠A+∠B+∠C=∠EDF+∠FDC+∠EDB,而∠EDF+∠FDC+∠EDB=180°,故∠A+∠B+∠C=180°。
24、(1)解:∵∠B=35°,∠ACB=85°,∴∠BAC=60°.
∵AD平分∠BAC,
∴∠DAC=30°.
∴∠ADC=65°.
又∵PE⊥AD,
∴∠DPE=90°.
∴∠E=25°.
(2)证明:∵∠B+∠BAC+∠ACB=180°,
∴∠BAC=180°-(∠B+∠ACB).
∵AD平分∠BAC,
∴∠BAD=∠BAC=90°-(∠B+∠ACB).
∴∠ADC=∠B+∠BAD=90°-(∠ACB-∠B).
∵PE⊥AD,
∴∠DPE=90°.
∴∠ADC+∠E=90°.
∴∠E=90°-∠ADC.
∴∠E=(∠ACB-∠B).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
