11.2.2 三角形的外角课时达标(含答案)
文档属性
| 名称 | 11.2.2 三角形的外角课时达标(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
11.2.2三角形的外角课时达标
一、选择题
如图,△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于(
)
?
A.
100°??????
B.
120°????
C.
130°????
D.
150°
2、若一个三角形的一个外角小于与它相邻的内角,则这个三角形是(
?
??
)
A.?直角三角形?????????B.?锐角三角形???
C.?钝角三角形?????????D.?无法确定
3、在△ABC中,∠A、∠B的外角分别是l20°、l50°,则∠C等于(???)
A.120°??
????B.156°
????C.60°??
???D.90°
4、如图,分别延长△ABC的三边BA、CB、AC,则=(?
)
A.180?
??????
B.270????
?
C.360?
?????
D.不能确定????????
5、如图,小林从P点向西直走12米后,向左转,转动的角度为,再走12米,如此重复,小林共走了108米回到点P,则(???
)
?
A.300?
????
B.400??
C.800????
D.不存在
6、如图,AB//CD,且∠D=150,∠E=250,则∠B的度数是(???
)?
A.300??????
B.500?????
C.400???????D.600?
7、如图,将三角尺的直角顶点放在直尺的一边上,∠1=300,∠2=500,则∠3的度数等于(???
)
A.500?????????
B.300???????
C.200???????
D.150
已知等腰三角形的一个外角为1000,则这个等腰三角形的顶角为(????
)
A.800??????????B.400????????
C.200或800??????D.200?
二、填空题
9、如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD= .?
10、把一副三角板按如图所示的方式摆放,则两条斜边所成的钝角x为 .?
11、如图,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A=________.
12、如图,∠A+∠B+∠C+∠D+∠E+∠F=________.
13、如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .?
14、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ,则有:
(1)∠A1=________;(2)∠An=________.
三、解答题
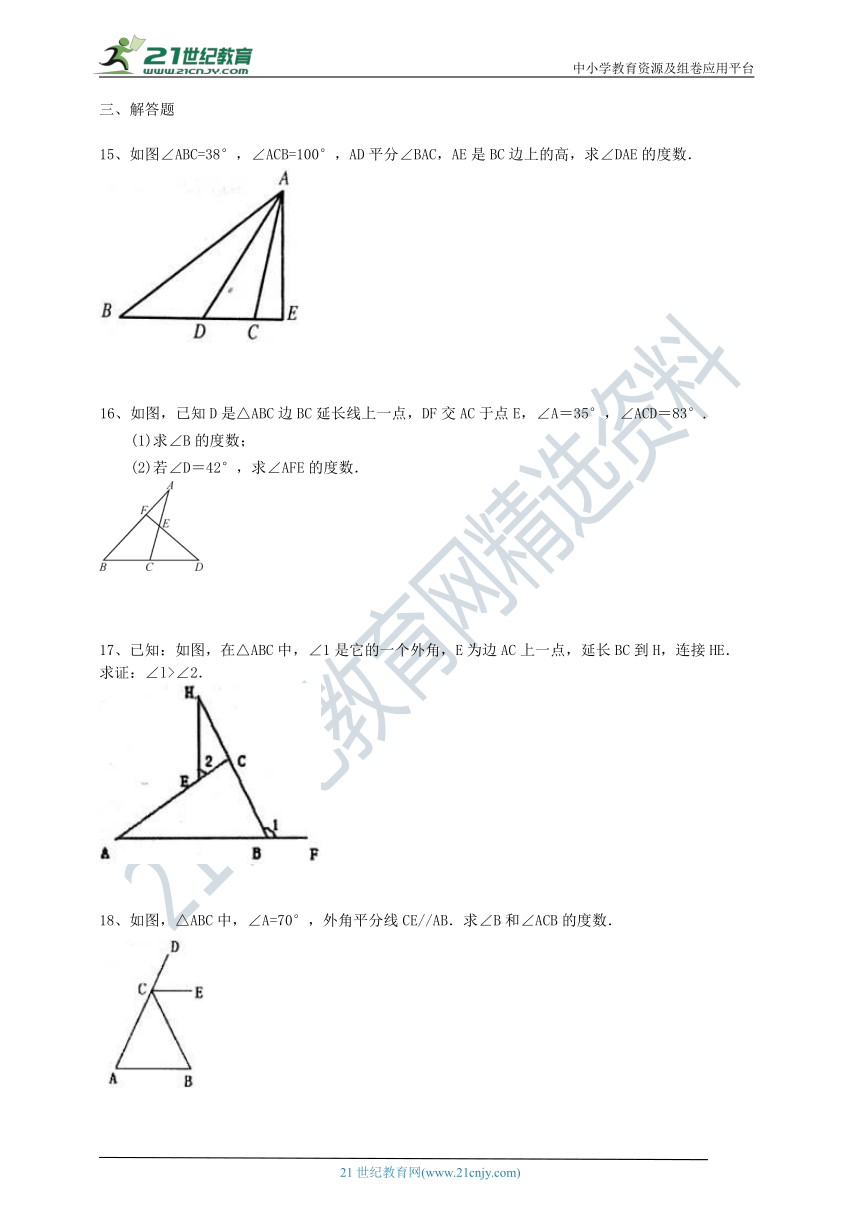
15、如图∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
16、如图,已知D是△ABC边BC延长线上一点,DF交AC于点E,∠A=35°,∠ACD=83°.
(1)求∠B的度数;
(2)若∠D=42°,求∠AFE的度数.
17、已知:如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到H,连接HE.
求证:∠l>∠2.
18、如图,△ABC中,∠A=70°,外角平分线CE//AB.求∠B和∠ACB的度数.
19、⊿ABC中,∠ABC、∠ACB的平分线相交于点O。
(1)若∠ABC
=
40°,∠ACB
=
50°,则∠BOC
=
???????????。
(2)若∠ABC
+∠ACB
=116°,则∠BOC
=???????????
。
(3)若∠A
=
76°,则∠BOC
=??????????
。
(4)若∠BOC
=
120°,则∠A
=
??????????。
(5)你能找出∠A与∠BOC
之间的数量关系吗?
?
20、动手操作,探究:(第⑴问2分、第⑵问5分、第⑶问5分,共12分)
如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系是_____??????
????????__.
研究(2):若折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):若折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
21、如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:??????
;
(2)仔细观察,在图2中“8字形”的个数:?????
个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠P与∠D、∠B之间数量关系,并说明理由。
参考答案
一、选择题
1、C
2、C??
3、D
4、C
5、B
6、C
7、C
8、C
二、填空题
9、150°
10、165°
11、10° 【点拨】设∠A=x.∵AB=BC=CD=DE=EF=FG,∴根据等腰三角形的性质和三角形的外角的性质,得∠CDB=∠CBD=2x,∠DEC=∠DCE=3x,∠DFE=∠EDF=4x,∠FGE=∠FEG=5x,∴180°-5x=130°,解得x=10°.∴∠A=10°.
12、360°
13、70°
(1)
(2)
三、解答题
16、解:(1)∵∠ACD是△ABC的一个外角,∠A=35°,∠ACD=83°
∴∠B=∠ACD-∠A=48°
(2)∵∠AFE是△BDF的一个外角,∠B=48°,∠D=42°
∴∠AFD=∠B+∠D=48°+42°=90°
17、证明:∵∠1是△ABC的一个外角
∴∠1>∠BCA
∵∠BCA是△HEC的一个外角
∴∠BCA>∠2
∴∠1>∠2
18、∠B=70°,∠ACB=40°
19、(1)135°;(2)122°;(3)128°;(4)60°;(5)∠BOC
=
90°+
∠A
20、(1)∠BDA′=2∠A?????????????????????????????????
(2)
∠BDA′+
∠CEA′=2∠A?????????????????
理由:在四边形AD
A′E中,
∠A+∠AD
A′+∠D
A′E+∠A′EA=360°
∴∠A+∠D
A′E=360°-∠AD
A′-∠A′EA
∵∠BDA′+∠AD
A′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠AD
A′+∠CEA′+∠A′EA=360°
∴∠BDA′+
∠CEA′=360°-∠AD
A′-∠A′EA
∴∠BDA′+
∠CEA′=∠A+∠D
A′E
∵△
A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠D
A′E
∴∠BDA′+
∠CEA′=2∠A
(3)∠BDA′-∠CEA′=2∠A
理由:∵∠BDA′=∠A+∠DFA,∠DFA=∠
A′+∠CEA′
???∴∠BDA′=∠A+∠
A′+∠CEA′
??
∴∠BDA′-∠CEA′=∠A+∠
A′
∵△
A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠D
A′E
∴∠BDA′-∠CEA′=2∠A
21、解:(1)结论:∠A+∠D=∠C+∠B
(2)结论:六个
(3)由∠D+∠1+∠2=∠B+∠3+∠4①(∵∠AOD=∠COB)
由∠1=∠2,∠3=∠4,
∴40°+2∠1=36°+2∠3
∴∠3-∠1=2°(1)
由∠ONC=∠B+∠4=∠P+∠2,②
∴∠P=∠B+∠4-∠2=36°+2°=38°
(4)由①∠D+2∠1=∠B+2∠3,
由②2∠B+2∠3=2∠P+2∠1
①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1
∠D+2∠B=2∠P+∠B.
∴∠P=
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.2.2三角形的外角课时达标
一、选择题
如图,△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于(
)
?
A.
100°??????
B.
120°????
C.
130°????
D.
150°
2、若一个三角形的一个外角小于与它相邻的内角,则这个三角形是(
?
??
)
A.?直角三角形?????????B.?锐角三角形???
C.?钝角三角形?????????D.?无法确定
3、在△ABC中,∠A、∠B的外角分别是l20°、l50°,则∠C等于(???)
A.120°??
????B.156°
????C.60°??
???D.90°
4、如图,分别延长△ABC的三边BA、CB、AC,则=(?
)
A.180?
??????
B.270????
?
C.360?
?????
D.不能确定????????
5、如图,小林从P点向西直走12米后,向左转,转动的角度为,再走12米,如此重复,小林共走了108米回到点P,则(???
)
?
A.300?
????
B.400??
C.800????
D.不存在
6、如图,AB//CD,且∠D=150,∠E=250,则∠B的度数是(???
)?
A.300??????
B.500?????
C.400???????D.600?
7、如图,将三角尺的直角顶点放在直尺的一边上,∠1=300,∠2=500,则∠3的度数等于(???
)
A.500?????????
B.300???????
C.200???????
D.150
已知等腰三角形的一个外角为1000,则这个等腰三角形的顶角为(????
)
A.800??????????B.400????????
C.200或800??????D.200?
二、填空题
9、如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD= .?
10、把一副三角板按如图所示的方式摆放,则两条斜边所成的钝角x为 .?
11、如图,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A=________.
12、如图,∠A+∠B+∠C+∠D+∠E+∠F=________.
13、如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .?
14、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ,则有:
(1)∠A1=________;(2)∠An=________.
三、解答题
15、如图∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
16、如图,已知D是△ABC边BC延长线上一点,DF交AC于点E,∠A=35°,∠ACD=83°.
(1)求∠B的度数;
(2)若∠D=42°,求∠AFE的度数.
17、已知:如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到H,连接HE.
求证:∠l>∠2.
18、如图,△ABC中,∠A=70°,外角平分线CE//AB.求∠B和∠ACB的度数.
19、⊿ABC中,∠ABC、∠ACB的平分线相交于点O。
(1)若∠ABC
=
40°,∠ACB
=
50°,则∠BOC
=
???????????。
(2)若∠ABC
+∠ACB
=116°,则∠BOC
=???????????
。
(3)若∠A
=
76°,则∠BOC
=??????????
。
(4)若∠BOC
=
120°,则∠A
=
??????????。
(5)你能找出∠A与∠BOC
之间的数量关系吗?
?
20、动手操作,探究:(第⑴问2分、第⑵问5分、第⑶问5分,共12分)
如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系是_____??????
????????__.
研究(2):若折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):若折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
21、如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:??????
;
(2)仔细观察,在图2中“8字形”的个数:?????
个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠P与∠D、∠B之间数量关系,并说明理由。
参考答案
一、选择题
1、C
2、C??
3、D
4、C
5、B
6、C
7、C
8、C
二、填空题
9、150°
10、165°
11、10° 【点拨】设∠A=x.∵AB=BC=CD=DE=EF=FG,∴根据等腰三角形的性质和三角形的外角的性质,得∠CDB=∠CBD=2x,∠DEC=∠DCE=3x,∠DFE=∠EDF=4x,∠FGE=∠FEG=5x,∴180°-5x=130°,解得x=10°.∴∠A=10°.
12、360°
13、70°
(1)
(2)
三、解答题
16、解:(1)∵∠ACD是△ABC的一个外角,∠A=35°,∠ACD=83°
∴∠B=∠ACD-∠A=48°
(2)∵∠AFE是△BDF的一个外角,∠B=48°,∠D=42°
∴∠AFD=∠B+∠D=48°+42°=90°
17、证明:∵∠1是△ABC的一个外角
∴∠1>∠BCA
∵∠BCA是△HEC的一个外角
∴∠BCA>∠2
∴∠1>∠2
18、∠B=70°,∠ACB=40°
19、(1)135°;(2)122°;(3)128°;(4)60°;(5)∠BOC
=
90°+
∠A
20、(1)∠BDA′=2∠A?????????????????????????????????
(2)
∠BDA′+
∠CEA′=2∠A?????????????????
理由:在四边形AD
A′E中,
∠A+∠AD
A′+∠D
A′E+∠A′EA=360°
∴∠A+∠D
A′E=360°-∠AD
A′-∠A′EA
∵∠BDA′+∠AD
A′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠AD
A′+∠CEA′+∠A′EA=360°
∴∠BDA′+
∠CEA′=360°-∠AD
A′-∠A′EA
∴∠BDA′+
∠CEA′=∠A+∠D
A′E
∵△
A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠D
A′E
∴∠BDA′+
∠CEA′=2∠A
(3)∠BDA′-∠CEA′=2∠A
理由:∵∠BDA′=∠A+∠DFA,∠DFA=∠
A′+∠CEA′
???∴∠BDA′=∠A+∠
A′+∠CEA′
??
∴∠BDA′-∠CEA′=∠A+∠
A′
∵△
A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠D
A′E
∴∠BDA′-∠CEA′=2∠A
21、解:(1)结论:∠A+∠D=∠C+∠B
(2)结论:六个
(3)由∠D+∠1+∠2=∠B+∠3+∠4①(∵∠AOD=∠COB)
由∠1=∠2,∠3=∠4,
∴40°+2∠1=36°+2∠3
∴∠3-∠1=2°(1)
由∠ONC=∠B+∠4=∠P+∠2,②
∴∠P=∠B+∠4-∠2=36°+2°=38°
(4)由①∠D+2∠1=∠B+2∠3,
由②2∠B+2∠3=2∠P+2∠1
①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1
∠D+2∠B=2∠P+∠B.
∴∠P=
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
