11.3.1 多边形课时达标(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
11.3.1多边形课时达标
一、选择题
1、下列图形中,多边形有( )
A.1个?????????
B.2个?????????
C.3个?????????
D.
4个
2、下列图形中,是正多边形的是(
)
A.等腰三角形?????
B.长方形
C.正方形????????D.五边都相等的五边形
3、下列各图中,是凸多边形的是(
)
4、下列说法正确的是(
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
5、一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形??
?
B.四边形?
??
C.五边形??
???
D.六边形
6、一个多边形有9条对角线,则这个多边形有多少条边( )
A.6?????
B.7??????
C.8????????
D.9
7、从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n??????B.n﹣1??????C.n﹣2??????
D.n﹣3
8、把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A.六边形????B.五边形?????C.四边形??????D.三角形
9、若一个一般的四边形的一组对角都是直角,则另一组对角可以(??
)
A.都是钝角
B.都是锐角
C.是一个锐角和一个直角
D.是一个锐角和一个钝角
二、填空题
10、从四边形的一个顶点出发可画 _________条对角线,从五边形的一个顶点出发可画_________条对角线,从六边形的一个顶点出发可画_________条对角线,请猜想从七边形的一个顶点出发有_________条对角线,从n边形的一个顶点出发有_________条对角线,从而推导出n边形共有_________条对角线.
11、一个凸多边形的内角中,最多有_________个锐角.
12、过m边形的一个顶点有4条对角线,n边形没有对角线,p边形有p条对角线,则(m-p)n=_________
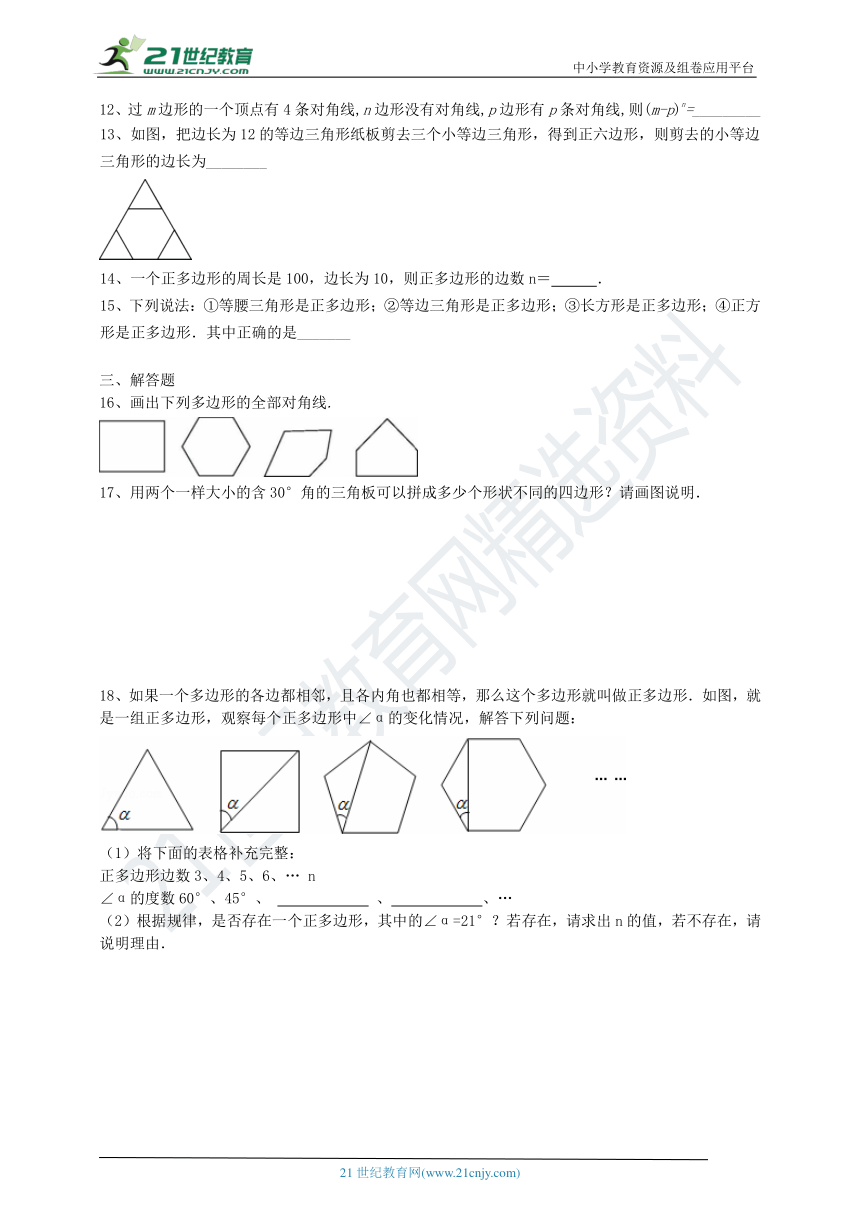
13、如图,把边长为12的等边三角形纸板剪去三个小等边三角形,得到正六边形,则剪去的小等边三角形的边长为________
14、一个正多边形的周长是100,边长为10,则正多边形的边数n=
.
15、下列说法:①等腰三角形是正多边形;②等边三角形是正多边形;③长方形是正多边形;④正方形是正多边形.其中正确的是_______
三、解答题
16、画出下列多边形的全部对角线.
17、用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.
18、如果一个多边形的各边都相邻,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数3、4、5、6、…
n
∠α的度数60°、45°、
、 、…
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
19、Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=?(n2﹣an+b)(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5=
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
20、观察下面图形,并回答问题.
(1)四边形有
条对角线;五边形有
条对角线;六边形有
条对角线.?
(2)根据规律七边形有
条对角线,n边形有? 条对角线.?
(3)为丰富学生的课余生活,合肥市第一中学8个班级之间举行篮球赛活动,如果采取单循环比赛(每两个班级之间只进行一场比赛),则篮球赛共需赛多少场?
参考答案
一、选择题
1、B
2、C
3、D
4、B
5、D?
?
6、A
7、C
8、A
9、D
二、填空题
10、解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有条对角线,
故答案为:1;2;3;4;(n﹣3);.
11、3
12、8
?
13、
4
14、
10
15、②④
解答题
16、解:如图所示.
17、解:四个.如图所示:
19、【考点】作图—应用与设计作图;二元一次方程的应用;多边形的对角线.
【分析】(1)依题意画出图形,数出图形中对角线交点的个数即可得出结论;
(2)将(1)中的数值代入公式可得出关于a、b的二元一次方程组,解方程组即可得出结论.
【解答】解:(1)画出图形如下.
由画形,可得:
当n=4时,P4=1;当n=5时,P5=5.
故答案为:1;5.
将(1)中的数值代入公式,得:
,
解得:
20、2?
5?
9
14
.
解:(3)当n=8时,=20(场),
答:篮球赛共需赛20场.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.3.1多边形课时达标
一、选择题
1、下列图形中,多边形有( )
A.1个?????????
B.2个?????????
C.3个?????????
D.
4个
2、下列图形中,是正多边形的是(
)
A.等腰三角形?????
B.长方形
C.正方形????????D.五边都相等的五边形
3、下列各图中,是凸多边形的是(
)
4、下列说法正确的是(
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
5、一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形??
?
B.四边形?
??
C.五边形??
???
D.六边形
6、一个多边形有9条对角线,则这个多边形有多少条边( )
A.6?????
B.7??????
C.8????????
D.9
7、从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n??????B.n﹣1??????C.n﹣2??????
D.n﹣3
8、把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A.六边形????B.五边形?????C.四边形??????D.三角形
9、若一个一般的四边形的一组对角都是直角,则另一组对角可以(??
)
A.都是钝角
B.都是锐角
C.是一个锐角和一个直角
D.是一个锐角和一个钝角
二、填空题
10、从四边形的一个顶点出发可画 _________条对角线,从五边形的一个顶点出发可画_________条对角线,从六边形的一个顶点出发可画_________条对角线,请猜想从七边形的一个顶点出发有_________条对角线,从n边形的一个顶点出发有_________条对角线,从而推导出n边形共有_________条对角线.
11、一个凸多边形的内角中,最多有_________个锐角.
12、过m边形的一个顶点有4条对角线,n边形没有对角线,p边形有p条对角线,则(m-p)n=_________
13、如图,把边长为12的等边三角形纸板剪去三个小等边三角形,得到正六边形,则剪去的小等边三角形的边长为________
14、一个正多边形的周长是100,边长为10,则正多边形的边数n=
.
15、下列说法:①等腰三角形是正多边形;②等边三角形是正多边形;③长方形是正多边形;④正方形是正多边形.其中正确的是_______
三、解答题
16、画出下列多边形的全部对角线.
17、用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.
18、如果一个多边形的各边都相邻,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数3、4、5、6、…
n
∠α的度数60°、45°、
、 、…
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
19、Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=?(n2﹣an+b)(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5=
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
20、观察下面图形,并回答问题.
(1)四边形有
条对角线;五边形有
条对角线;六边形有
条对角线.?
(2)根据规律七边形有
条对角线,n边形有? 条对角线.?
(3)为丰富学生的课余生活,合肥市第一中学8个班级之间举行篮球赛活动,如果采取单循环比赛(每两个班级之间只进行一场比赛),则篮球赛共需赛多少场?
参考答案
一、选择题
1、B
2、C
3、D
4、B
5、D?
?
6、A
7、C
8、A
9、D
二、填空题
10、解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有条对角线,
故答案为:1;2;3;4;(n﹣3);.
11、3
12、8
?
13、
4
14、
10
15、②④
解答题
16、解:如图所示.
17、解:四个.如图所示:
19、【考点】作图—应用与设计作图;二元一次方程的应用;多边形的对角线.
【分析】(1)依题意画出图形,数出图形中对角线交点的个数即可得出结论;
(2)将(1)中的数值代入公式可得出关于a、b的二元一次方程组,解方程组即可得出结论.
【解答】解:(1)画出图形如下.
由画形,可得:
当n=4时,P4=1;当n=5时,P5=5.
故答案为:1;5.
将(1)中的数值代入公式,得:
,
解得:
20、2?
5?
9
14
.
解:(3)当n=8时,=20(场),
答:篮球赛共需赛20场.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
