11.3.2 多边形的内角和课时达标(含答案)
文档属性
| 名称 | 11.3.2 多边形的内角和课时达标(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.3.2多边形的内角和课时达标
一、选择题
1、一个n边形的内角和为900°,则n等于( )
A.5
???
????
B.6
??????
???
C.7
???
???
?
???
D.8
2、正八边形的每个内角为(
)
A.1200???????B.1350????????C.1400???????????D.1440?
3、已知一个多边形的内角和比它的外角和的3倍多180°,则这个多边形是(
)
A.九边形
??????B.八边形
???????C.七边形
??????
D.六边形
4、正多边形的一个内角是120°,则这个正多边形的边数为(
)
A.4
??
B.8?
??
C.6?
??
D.12
5、在美丽的明清宫广场中心地带整修工程中,计划采用同一种正多边形地板砖铺设地面,在下面的地板砖:①正方形,②正五边形,③正六边形,④正八边形中能够铺满地面的地板砖的种数是(
)
A.1??????
B.2????
C.3??????
D.4
6、一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为(?
)
A.13???????B.15??????
C.13或15???????
D.15或16或17
7、若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为(???
)
A.90°??????B.105°
C.130°??????????
D.120°
二、填空题
8、一个多边形的每个外角都等于720?,则这个多边形的边数为__________.
9、将一个n边形变成n+1边形,其内角和________,外角和________.
10、如图,正六边形ABCDEF,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N,则∠MPN=_______.
11、如图,在同一平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则∠3+∠1-∠2=________.
三、解答题
12、求图中的x值.
???
13、如图,已知正五边形ABCDE的每一个角都相等.
(1)求∠B的度数;
(2)连接AC,若∠BAC=∠BCA,求∠ACD的度数.
?
14、请根据下面x与y的对话解答下列各小题:
X:我和y都是多边形,我们俩的内角和相加的结果为1440°;
Y:x的边数与我的边数之比为1:3.
(1)求x与y的外角和相加的度数?
(2)分别求出x与y的边数?
(3)试求出y共有多少条对角线?
15、已知两个多边形的内角和之和为1
800°,且两多边形的边数之比为2∶5,求这两个多边形的边数.
16、多边形的内角和与某一个外角的度数总和为1
350°,求多边形的边数.
17、已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
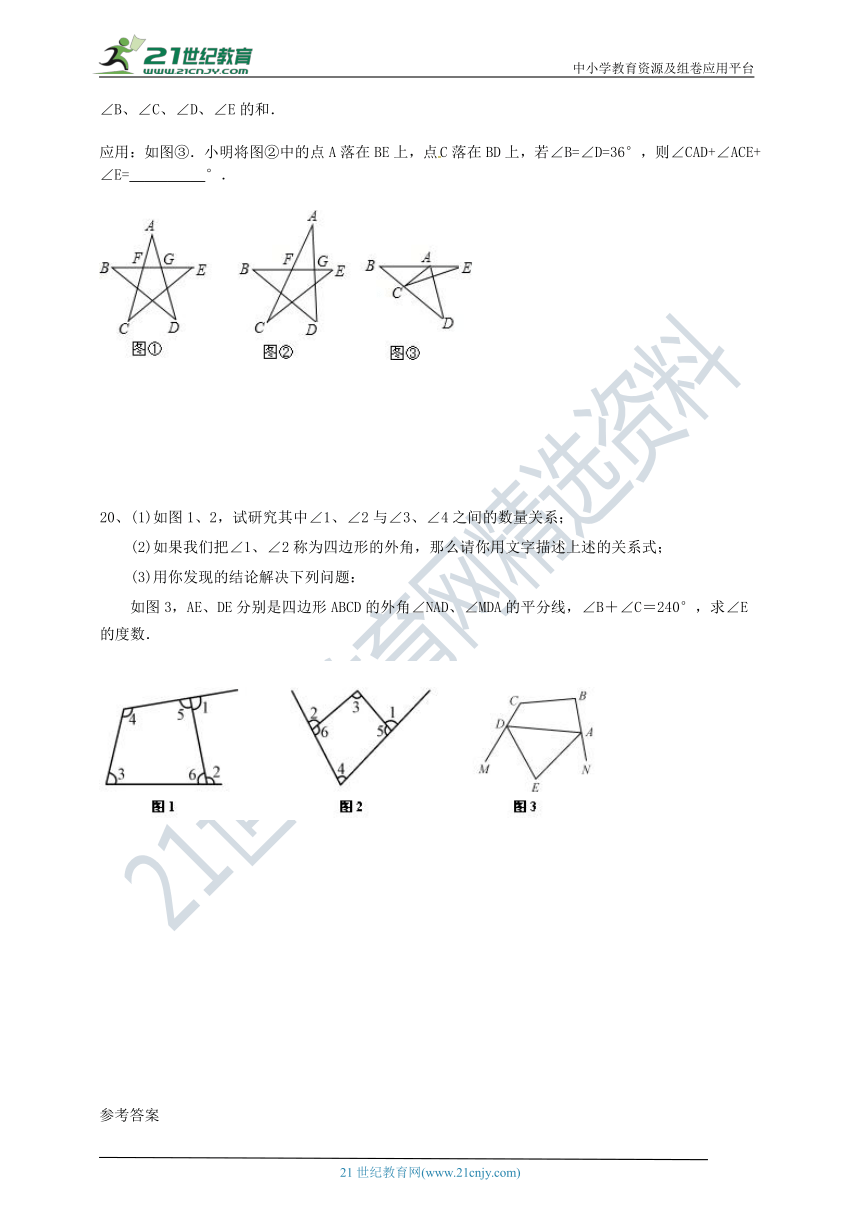
18、探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=__________°,
∴∠A+∠B+∠C+∠D+∠E=__________°,
∴∠A=∠B=∠C=∠D=∠E=__________°.
19、拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
20、(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
参考答案
一、选择题
1、C
2、B
3、A
4、C
5、B
6、D?
7、C
二、填空题
8、5
9、增加180°、不变
10、60°
11、24°
三、解答题
13、解:(1)正五边形ABCDE的内角和是(5-2)×1800=5400,则
(2)在△ABC中,∵∠BAC=∠BCA,∴
∴∠ACD=∠BCD-∠BCA=1080-360=720
14、【考点】多边形内角与外角.
【分析】(1)根据多边形的外角和定理可得多边形的外角和为360°,进而可得答案;
(2)设X的边数为n,Y的边数为3n,根据多边形的内角和定理结合题意可得方程180(n﹣2)+180(3n﹣2)=1440,解出X的值,进而可得n的值,然后可得答案;
(3)根据求多边形的对角线的公式即可得到结果.
【解答】解:(1)360°+360°=720°;
(2)设X的边数为n,Y的边数为3n,由题意得:
180(n﹣2)+180(3n﹣2)=1440,
解得:n=3,
∴3n=9,
∴x与y的边数分别为3和9;
(3)×9×(9﹣3)=27条,
答:y共有27条对角线.
【点评】本题主要考查的是多边形的内角与外角,掌握多边形的内角和公式与外角和定理是解题的关键.
15、解:设两多边形的边数分别为2n和5n,
则它们的内角和分别为(2n-2)×180°和(5n-2)×180°,
则(2n-2)×180°+(5n-2)×180°=1
800°,
解得n=2.
2n=4,5n=10.
答:这两个多边形的边数分别为4,10.
16、解:设这个外角度数为x°,多边形的边数为n.由题意,得
(n-2)×180+x=1
350.
解得x=1
710-180n.
∵0<x<180,
∴0<1
710-180n<180.
解得8.5<n<9.5.
又∵n为正整数,∴n=9.
故多边形的边数是9.
17、解:(1)甲对,乙不对.理由:
∵θ=360°,∴(n-2)×180=360,解得n=4.
∵θ=630°,∴(n-2)×180=630,解得n=.
∵n为整数,∴θ不能取630°.
(2)依题意得(n-2)×180+360=(n+x-2)×180,解得x=2.
18、【考点】三角形的外角性质;三角形内角和定理.
【专题】探究型.
【分析】根据阅读材料、三角形内角和定理、三角形的外角的性质、结合图形解得即可.
【解答】解:探究:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴∠A=∠B=∠C=∠D=∠E=36°;
拓展:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°
应用:∠CAD+∠ACE+∠E=180°﹣∠EAD=180°﹣∠B﹣∠D=108°.
【点评】本题考查的是三角形内角和定理、三角形外角的性质,掌握三角形内角和等于180°和三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
19、解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.
∴∠E=180°-(∠ADE+∠DAE)=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.3.2多边形的内角和课时达标
一、选择题
1、一个n边形的内角和为900°,则n等于( )
A.5
???
????
B.6
??????
???
C.7
???
???
?
???
D.8
2、正八边形的每个内角为(
)
A.1200???????B.1350????????C.1400???????????D.1440?
3、已知一个多边形的内角和比它的外角和的3倍多180°,则这个多边形是(
)
A.九边形
??????B.八边形
???????C.七边形
??????
D.六边形
4、正多边形的一个内角是120°,则这个正多边形的边数为(
)
A.4
??
B.8?
??
C.6?
??
D.12
5、在美丽的明清宫广场中心地带整修工程中,计划采用同一种正多边形地板砖铺设地面,在下面的地板砖:①正方形,②正五边形,③正六边形,④正八边形中能够铺满地面的地板砖的种数是(
)
A.1??????
B.2????
C.3??????
D.4
6、一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为(?
)
A.13???????B.15??????
C.13或15???????
D.15或16或17
7、若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为(???
)
A.90°??????B.105°
C.130°??????????
D.120°
二、填空题
8、一个多边形的每个外角都等于720?,则这个多边形的边数为__________.
9、将一个n边形变成n+1边形,其内角和________,外角和________.
10、如图,正六边形ABCDEF,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N,则∠MPN=_______.
11、如图,在同一平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则∠3+∠1-∠2=________.
三、解答题
12、求图中的x值.
???
13、如图,已知正五边形ABCDE的每一个角都相等.
(1)求∠B的度数;
(2)连接AC,若∠BAC=∠BCA,求∠ACD的度数.
?
14、请根据下面x与y的对话解答下列各小题:
X:我和y都是多边形,我们俩的内角和相加的结果为1440°;
Y:x的边数与我的边数之比为1:3.
(1)求x与y的外角和相加的度数?
(2)分别求出x与y的边数?
(3)试求出y共有多少条对角线?
15、已知两个多边形的内角和之和为1
800°,且两多边形的边数之比为2∶5,求这两个多边形的边数.
16、多边形的内角和与某一个外角的度数总和为1
350°,求多边形的边数.
17、已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
18、探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=__________°,
∴∠A+∠B+∠C+∠D+∠E=__________°,
∴∠A=∠B=∠C=∠D=∠E=__________°.
19、拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
20、(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
参考答案
一、选择题
1、C
2、B
3、A
4、C
5、B
6、D?
7、C
二、填空题
8、5
9、增加180°、不变
10、60°
11、24°
三、解答题
13、解:(1)正五边形ABCDE的内角和是(5-2)×1800=5400,则
(2)在△ABC中,∵∠BAC=∠BCA,∴
∴∠ACD=∠BCD-∠BCA=1080-360=720
14、【考点】多边形内角与外角.
【分析】(1)根据多边形的外角和定理可得多边形的外角和为360°,进而可得答案;
(2)设X的边数为n,Y的边数为3n,根据多边形的内角和定理结合题意可得方程180(n﹣2)+180(3n﹣2)=1440,解出X的值,进而可得n的值,然后可得答案;
(3)根据求多边形的对角线的公式即可得到结果.
【解答】解:(1)360°+360°=720°;
(2)设X的边数为n,Y的边数为3n,由题意得:
180(n﹣2)+180(3n﹣2)=1440,
解得:n=3,
∴3n=9,
∴x与y的边数分别为3和9;
(3)×9×(9﹣3)=27条,
答:y共有27条对角线.
【点评】本题主要考查的是多边形的内角与外角,掌握多边形的内角和公式与外角和定理是解题的关键.
15、解:设两多边形的边数分别为2n和5n,
则它们的内角和分别为(2n-2)×180°和(5n-2)×180°,
则(2n-2)×180°+(5n-2)×180°=1
800°,
解得n=2.
2n=4,5n=10.
答:这两个多边形的边数分别为4,10.
16、解:设这个外角度数为x°,多边形的边数为n.由题意,得
(n-2)×180+x=1
350.
解得x=1
710-180n.
∵0<x<180,
∴0<1
710-180n<180.
解得8.5<n<9.5.
又∵n为正整数,∴n=9.
故多边形的边数是9.
17、解:(1)甲对,乙不对.理由:
∵θ=360°,∴(n-2)×180=360,解得n=4.
∵θ=630°,∴(n-2)×180=630,解得n=.
∵n为整数,∴θ不能取630°.
(2)依题意得(n-2)×180+360=(n+x-2)×180,解得x=2.
18、【考点】三角形的外角性质;三角形内角和定理.
【专题】探究型.
【分析】根据阅读材料、三角形内角和定理、三角形的外角的性质、结合图形解得即可.
【解答】解:探究:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴∠A=∠B=∠C=∠D=∠E=36°;
拓展:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°
应用:∠CAD+∠ACE+∠E=180°﹣∠EAD=180°﹣∠B﹣∠D=108°.
【点评】本题考查的是三角形内角和定理、三角形外角的性质,掌握三角形内角和等于180°和三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
19、解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.
∴∠E=180°-(∠ADE+∠DAE)=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
