人教版七年级上册数学课件:1.4.1有理数的乘法(共16张PPT)
文档属性
| 名称 | 人教版七年级上册数学课件:1.4.1有理数的乘法(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 10:32:57 | ||
图片预览






文档简介
(共16张PPT)
有理数的乘法
一、目标展示
1、理解掌握有理数的乘法法则
2、能够运用有理数的乘法法则进行有关计算
3×3=
;
3×2=
;
3×1=
;
3×0=
;
思考
观察下列算式,你能发现什么规律?
9
6
3
0
3×3=
;
2×3=
;
1×3=
;
0×3=
;
9
6
3
0
(-3)×3
=
;
(-3)×2
=
;
(-3)×1
=
;
(-3)×0
=
;
-9
-6
-3
0
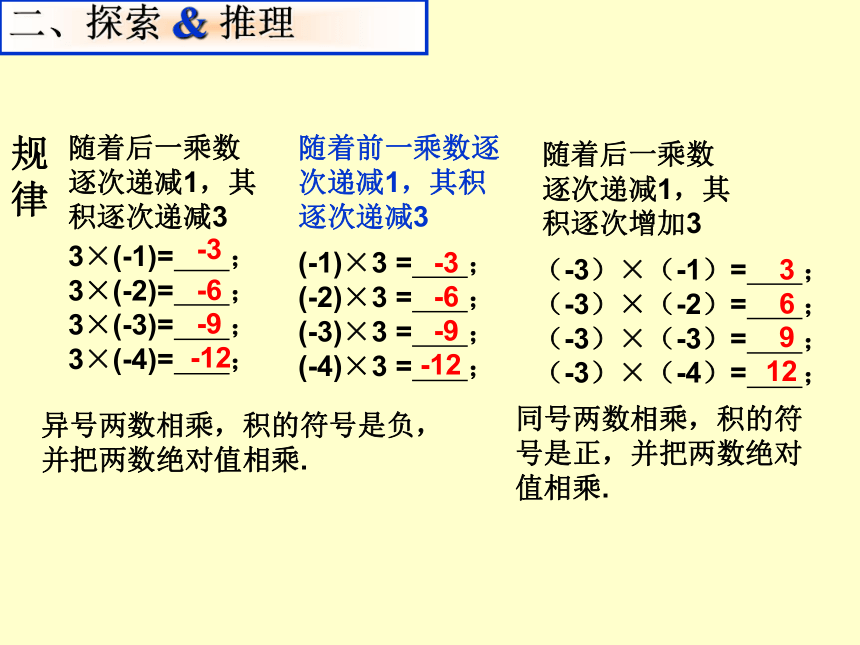
二、探索
&
推理
(-1)×3
=
;
(-2)×3
=
;
(-3)×3
=
;
(-4)×3
=
;
(-3)×(-1)=
;
(-3)×(-2)=
;
(-3)×(-3)=
;
(-3)×(-4)=
;
规律
随着后一乘数逐次递减1,其积逐次递减3
3×(-1)=
;
3×(-2)=
;
3×(-3)=
;
3×(-4)=
;
-3
-6
-9
-12
随着前一乘数逐次递减1,其积逐次递减3
-3
-6
-9
-12
异号两数相乘,积的符号是负,并把两数绝对值相乘.
随着后一乘数逐次递减1,其积逐次增加3
3
6
9
12
同号两数相乘,积的符号是正,并把两数绝对值相乘.
二、探索
&
推理
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
认真记呦!
任何数同0相乘,都得0。
三、归纳
&
总结
(1)(-5)×(-6)
(2)(-
)×
=
+
=
30
(5
×6)
=
-
有理数相乘,先确定积的符号,再确定积的绝对值。
例1
计算:
解:
(1)(-5)×(-6)
四、例题
详解
(1)
0.5 ×
0.7
(2)(-4)
×
6
(3)
5
×
(-3)
(4)
(-7)
×
(-9)
(5)(-
)×4
(6
)(-3)
×(-
)
=-15
=
63
=-24
=
0.35
=
=
-2
五、目标测试
&
反馈
1、计算:
2、计算:
(2)
8
×
(-1.25)
(1)(-
)
×
(-
)
(3)
(-a)
×b
(4)
(-m)
×(-n)
=
-ab
=
mn
=
1
=
10
五、目标测试
&
反馈
/14
=
24
结论:几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
几个数相乘,有一个为0,积就为0.
1、1×2×3×4
2、1×2×3×(-4)
=
-24
3、1×2×(-3)×(-4)
=
24
4、1×(-2)×(-3)×(-4)
=
-24
5、(-1)×(-2)×(-3)×(-4)
=
24
6、(-1)×(-2)×(-3)×(-4)
×0
=
0
六、推理
&
总结
(2)
(-8)
×2.5
×(-4)
3、
计算:
=
-126
(1)(-7)
×(-9)
×(-2)
=
80
七、目标测试
&
反馈
4
计算:
(3)
(1-2)
×(2-3)
×(3-4)
…(2005-2006)
七、目标测试
&
反馈
七、目标测试
&
反馈
6.填写下表:
七、目标测试
&
反馈
被乘数
乘数
积的符号
绝对值
结果
-5
7
15
6
-30
-6
4
-25
7.写出下列各数的倒数.
观察并讨论:
1)0有没有倒数?
2)一个数的倒数等于它本身,那么这个数是_______.
七、目标测试
&
反馈
有理数乘法法则
1、两数相乘,同号得正,异号得负,并把绝对值相乘。
2、任何数同0相乘,都得0。
3、几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
4、几个数相乘,有一个为0,积就为0.
八、目标
回顾
/12
课本
P:37
习题1.5
T:1
再见
!!走读的学生注意交通安全!!
有理数的乘法
一、目标展示
1、理解掌握有理数的乘法法则
2、能够运用有理数的乘法法则进行有关计算
3×3=
;
3×2=
;
3×1=
;
3×0=
;
思考
观察下列算式,你能发现什么规律?
9
6
3
0
3×3=
;
2×3=
;
1×3=
;
0×3=
;
9
6
3
0
(-3)×3
=
;
(-3)×2
=
;
(-3)×1
=
;
(-3)×0
=
;
-9
-6
-3
0
二、探索
&
推理
(-1)×3
=
;
(-2)×3
=
;
(-3)×3
=
;
(-4)×3
=
;
(-3)×(-1)=
;
(-3)×(-2)=
;
(-3)×(-3)=
;
(-3)×(-4)=
;
规律
随着后一乘数逐次递减1,其积逐次递减3
3×(-1)=
;
3×(-2)=
;
3×(-3)=
;
3×(-4)=
;
-3
-6
-9
-12
随着前一乘数逐次递减1,其积逐次递减3
-3
-6
-9
-12
异号两数相乘,积的符号是负,并把两数绝对值相乘.
随着后一乘数逐次递减1,其积逐次增加3
3
6
9
12
同号两数相乘,积的符号是正,并把两数绝对值相乘.
二、探索
&
推理
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
认真记呦!
任何数同0相乘,都得0。
三、归纳
&
总结
(1)(-5)×(-6)
(2)(-
)×
=
+
=
30
(5
×6)
=
-
有理数相乘,先确定积的符号,再确定积的绝对值。
例1
计算:
解:
(1)(-5)×(-6)
四、例题
详解
(1)
0.5 ×
0.7
(2)(-4)
×
6
(3)
5
×
(-3)
(4)
(-7)
×
(-9)
(5)(-
)×4
(6
)(-3)
×(-
)
=-15
=
63
=-24
=
0.35
=
=
-2
五、目标测试
&
反馈
1、计算:
2、计算:
(2)
8
×
(-1.25)
(1)(-
)
×
(-
)
(3)
(-a)
×b
(4)
(-m)
×(-n)
=
-ab
=
mn
=
1
=
10
五、目标测试
&
反馈
/14
=
24
结论:几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
几个数相乘,有一个为0,积就为0.
1、1×2×3×4
2、1×2×3×(-4)
=
-24
3、1×2×(-3)×(-4)
=
24
4、1×(-2)×(-3)×(-4)
=
-24
5、(-1)×(-2)×(-3)×(-4)
=
24
6、(-1)×(-2)×(-3)×(-4)
×0
=
0
六、推理
&
总结
(2)
(-8)
×2.5
×(-4)
3、
计算:
=
-126
(1)(-7)
×(-9)
×(-2)
=
80
七、目标测试
&
反馈
4
计算:
(3)
(1-2)
×(2-3)
×(3-4)
…(2005-2006)
七、目标测试
&
反馈
七、目标测试
&
反馈
6.填写下表:
七、目标测试
&
反馈
被乘数
乘数
积的符号
绝对值
结果
-5
7
15
6
-30
-6
4
-25
7.写出下列各数的倒数.
观察并讨论:
1)0有没有倒数?
2)一个数的倒数等于它本身,那么这个数是_______.
七、目标测试
&
反馈
有理数乘法法则
1、两数相乘,同号得正,异号得负,并把绝对值相乘。
2、任何数同0相乘,都得0。
3、几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
4、几个数相乘,有一个为0,积就为0.
八、目标
回顾
/12
课本
P:37
习题1.5
T:1
再见
!!走读的学生注意交通安全!!
