2012届高考复习方案数学理科(北师版)第2单元第10讲 幂函数与函数的图像
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第2单元第10讲 幂函数与函数的图像 |
|
|
| 格式 | rar | ||
| 文件大小 | 233.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 18:06:20 | ||
图片预览








文档简介
(共25张PPT)
第10讲 │ 幂函数与函数的图像
第10讲 幂函数与函数的图像
知识梳理
1.幂函数
(1)幂函数定义:一般地,形如______(α∈R)的函数称为幂函数,
其中α为常数.
几种常见幂函数的图像:
①y=x;②y=x;③y=x2;④y=x-1;⑤y=x3.
图10-1
第10讲 │ 知识梳理
y=xα
(2)幂函数性质
①所有的幂函数在______都有定义,并且图像都过点______;
②α>0时,幂函数的图像通过______,并且在区间[0,+∞)上是________.特别地,当α>1时,幂函数的图像______;当0<α<1时,幂函数的图像______;
③α<0时,幂函数的图像在区间(0,+∞)上是__________.在第一象限内,当x从右边趋向原点时,图像在y轴右方无限地逼近y轴正半轴,当x趋于+∞时,图像在x轴上方无限地逼近x轴正半轴.
第10讲 │ 知识梳理
(0,+∞)
(1,1)
原点
增函数
下凸
上凸
减函数
第10讲 │ 知识梳理
2.函数图像
以解析式表示的函数作图像的方法有两种,即____________和____________.
描点法:
(1)作函数图像的步骤:
①确定函数的________;
②化简函数的解析式;
③讨论函数的性质,即____________________________________________;
④描点连线,画出函数的图像.
列表描点法
图像变换法
定义域
单调性、奇偶性、周期性
第10讲 │ 知识梳理
x轴方向
平移|a|
关于y轴
原点
直线x=a
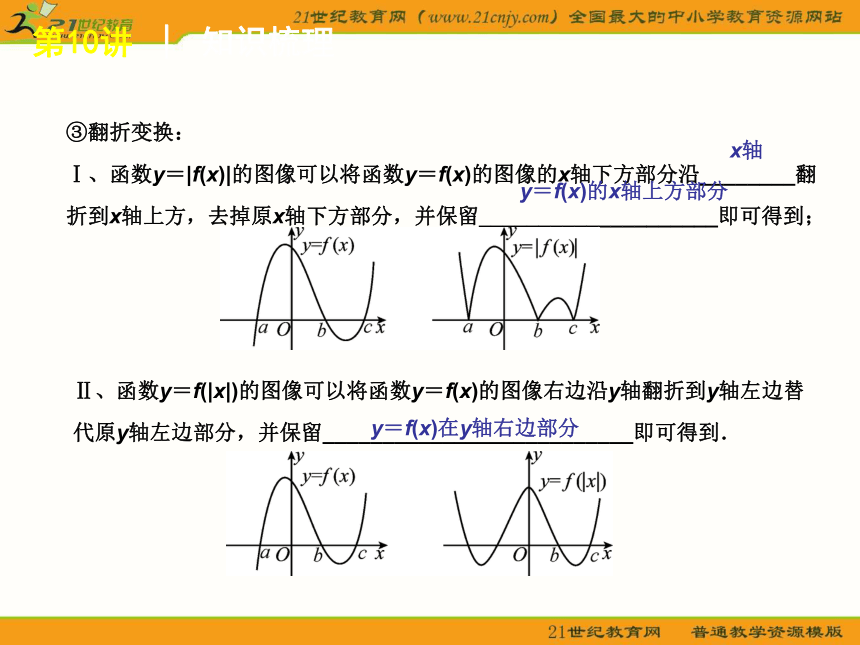
Ⅱ、函数y=f(|x|)的图像可以将函数y=f(x)的图像右边沿y轴翻折到y轴左边替代原y轴左边部分,并保留__________________________即可得到.
③翻折变换:
Ⅰ、函数y=|f(x)|的图像可以将函数y=f(x)的图像的x轴下方部分沿________翻折到x轴上方,去掉原x轴下方部分,并保留____________________即可得到;
第10讲 │ 知识梳理
x轴
y=f(x)的x轴上方部分
y=f(x)在y轴右边部分
第10讲 │ 知识梳理
纵坐标伸长(a>1)或压缩(0要点探究
探究点1 幂函数定义的应用
第10讲 │ 要点探究
[思路] 利用各类函数的定义,确定x的指数的取值
[解答] (1)由m2+2m=1,解得m=-1±.
(2)由m2-2m-1=1,得m=1±.
(3)由m2-2m-1=-1,m=0或m=2,又当m=0 时,m2+2m=0,不符合题意,舍去,故m=2.
探究点2 幂函数的图像与性质
第10讲 │ 要点探究
[思路]利用幂函数的奇偶性和单调性确定m的值,再由幂函数的单调性确定a的值
例2 已知幂函数f(x)=xm2-2m-3(m∈N*)的图像关于y轴对称,且在(0,+∞)上是减函数,求满足(a+1)<(3-2a)的a的取值范围.
第10讲 │ 要点探究
[点评] 本题集幂函数概念、图像及单调性、奇偶性于一体,综合性较强,解此题的关键是弄清幂函数的概念及性质.由幂函数的定义求参数的取值范围时,要注意检验求得的参数是否符合题意,如:
第10讲 │ 要点探究
[答案] 2
(1)函数f(x)=(m2-m-1)xm2-2m-3是幂函数,且当x∈(0,+∞)时是减函数,则m=________.
第10讲 │ 要点探究
(2)幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图10-4).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图像三等分,即有BM=MN=NA.那么αβ=__________.
图10-4
[答案] 1
探究点3 函数的图像的画法
[思路]根据各函数解析式的结构特征,分析其图像是由哪类初等函数经过何种变换而得
第10讲 │ 要点探究
第10讲 │ 要点探究
第10讲 │ 要点探究
第10讲 │ 要点探究
[点评] (1)利用描点法作函数图像的步骤是:列表、描点、连线,若对函数图像的形状比较熟悉,可不必列表,直接描点、连线;(2)利用图像变换作函数图像,关键是找出基本初等函数,将函数的解析式分解为只有单个变换的函数链,然后依次进行单一变换,最终得到所要的函数图像.
第10讲 │ 要点探究
[答案] ①⑧⑤或①③⑧或④⑧①或④①⑧(填一组即可)
[思路] 先确定图像变换的种类,然后确定图像变换的顺序
第10讲 │ 要点探究
[点评] 将函数f(x)经过多种图像变换得到g(x)的图像,可能有多种不同的顺序,但不管按哪种顺序进行变换,都必须遵循“只能对函数关系式中的x、y进行变换”的原则,否则容易出错.
探究点4 函数图像的识别与应用
例4 如图10-5所示,一质点P(x,y)在xOy平面上沿曲线运动,速度大小不变,其在x轴上的影点Q(x,0)的运动速度V=V(t)的图像大致为( )
第10讲 │ 要点探究
图10-5
第10讲 │ 要点探究
[思路] 从已知图形中封闭曲线入手,研究投影点Q(x,0)的速度的变化规律.
[答案] B
[解析] 由图可知,当质点P(x,y)在两个封闭曲线上运动时,投影点Q(x,0)的速度先由正到0、到负数,到负数,再到0,到正,故A错误,质点P(x,y)在开始时沿直线运动,故投影点Q(x,0)的速度为常数,因此C是错误的,故选B.
[点评] 函数图像是函数关系的直观表现,它可以形象的反映函数中变量间的变化关系,有助于我们对函数关系的直观理解和对函数性质的分析,处理函数问题时要心中有形.
第10讲 │ 要点探究
[答案] C
(1)有四个函数:①y=x·sinx;②y=x·cosx;③y=x·|cosx|;④y=x·2x的图像(部分)如下,但顺序被打乱,则按照从左到右将图像对应的函数序号安排正确的一组是( )
A.④①②③ B.①④③②
C.①④②③ D.③④②①
图10-7
[解析] (1)函数xsinx是偶函数,因此其图像只能是第一个,函数y=xcosx与y=x|cosx|都为奇函数,但当x>0时,y=x|cosx|≥0恒成立,故函数只能是第四个,函数y=x·2x不具有奇偶性,因此其图像只能是第二个,故选C.
第10讲 │ 要点探究
(2)如图10-8,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图像大致是( )
图10-8
图10-9
[答案] B
第10讲 │ 要点探究
规律总结
第10讲 │ 规律总结
1.幂函数y=xa的图像一定会出现在第一象限内,一定不会出现的第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;在(0,1)上,幂函数中指数愈大,函数图像愈靠近x轴,在(1,+∞)上,幂函数中指数越大,函数图像越远离x轴;幂函数的单调性、奇偶性由指数决定.
2.作图
作图的常用方法有描点法和变换法,对前者,要注意对函数性质的研究;对后者,要熟悉常见函数及图像的变换法则,在解决函数图像的变换问题时,要遵循“只能对函数关系式中的x、y变换”的原则,写出每一次的变换所得图像对应的解析式,这样才能避免出错.
第10讲 │ 规律总结
3.识图
对于给定函数的图像,要能从图像的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等,注意图像与函数解析式中参数的关系.
4.用图
函数图像形象地显示了函数的性质,为研究数量关系提供了“形”的直观性,它是探求解题路径,获得问题结果的重要工具,要重视数形结合思想的应用.
第10讲 │ 幂函数与函数的图像
第10讲 幂函数与函数的图像
知识梳理
1.幂函数
(1)幂函数定义:一般地,形如______(α∈R)的函数称为幂函数,
其中α为常数.
几种常见幂函数的图像:
①y=x;②y=x;③y=x2;④y=x-1;⑤y=x3.
图10-1
第10讲 │ 知识梳理
y=xα
(2)幂函数性质
①所有的幂函数在______都有定义,并且图像都过点______;
②α>0时,幂函数的图像通过______,并且在区间[0,+∞)上是________.特别地,当α>1时,幂函数的图像______;当0<α<1时,幂函数的图像______;
③α<0时,幂函数的图像在区间(0,+∞)上是__________.在第一象限内,当x从右边趋向原点时,图像在y轴右方无限地逼近y轴正半轴,当x趋于+∞时,图像在x轴上方无限地逼近x轴正半轴.
第10讲 │ 知识梳理
(0,+∞)
(1,1)
原点
增函数
下凸
上凸
减函数
第10讲 │ 知识梳理
2.函数图像
以解析式表示的函数作图像的方法有两种,即____________和____________.
描点法:
(1)作函数图像的步骤:
①确定函数的________;
②化简函数的解析式;
③讨论函数的性质,即____________________________________________;
④描点连线,画出函数的图像.
列表描点法
图像变换法
定义域
单调性、奇偶性、周期性
第10讲 │ 知识梳理
x轴方向
平移|a|
关于y轴
原点
直线x=a
Ⅱ、函数y=f(|x|)的图像可以将函数y=f(x)的图像右边沿y轴翻折到y轴左边替代原y轴左边部分,并保留__________________________即可得到.
③翻折变换:
Ⅰ、函数y=|f(x)|的图像可以将函数y=f(x)的图像的x轴下方部分沿________翻折到x轴上方,去掉原x轴下方部分,并保留____________________即可得到;
第10讲 │ 知识梳理
x轴
y=f(x)的x轴上方部分
y=f(x)在y轴右边部分
第10讲 │ 知识梳理
纵坐标伸长(a>1)或压缩(0
探究点1 幂函数定义的应用
第10讲 │ 要点探究
[思路] 利用各类函数的定义,确定x的指数的取值
[解答] (1)由m2+2m=1,解得m=-1±.
(2)由m2-2m-1=1,得m=1±.
(3)由m2-2m-1=-1,m=0或m=2,又当m=0 时,m2+2m=0,不符合题意,舍去,故m=2.
探究点2 幂函数的图像与性质
第10讲 │ 要点探究
[思路]利用幂函数的奇偶性和单调性确定m的值,再由幂函数的单调性确定a的值
例2 已知幂函数f(x)=xm2-2m-3(m∈N*)的图像关于y轴对称,且在(0,+∞)上是减函数,求满足(a+1)<(3-2a)的a的取值范围.
第10讲 │ 要点探究
[点评] 本题集幂函数概念、图像及单调性、奇偶性于一体,综合性较强,解此题的关键是弄清幂函数的概念及性质.由幂函数的定义求参数的取值范围时,要注意检验求得的参数是否符合题意,如:
第10讲 │ 要点探究
[答案] 2
(1)函数f(x)=(m2-m-1)xm2-2m-3是幂函数,且当x∈(0,+∞)时是减函数,则m=________.
第10讲 │ 要点探究
(2)幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图10-4).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图像三等分,即有BM=MN=NA.那么αβ=__________.
图10-4
[答案] 1
探究点3 函数的图像的画法
[思路]根据各函数解析式的结构特征,分析其图像是由哪类初等函数经过何种变换而得
第10讲 │ 要点探究
第10讲 │ 要点探究
第10讲 │ 要点探究
第10讲 │ 要点探究
[点评] (1)利用描点法作函数图像的步骤是:列表、描点、连线,若对函数图像的形状比较熟悉,可不必列表,直接描点、连线;(2)利用图像变换作函数图像,关键是找出基本初等函数,将函数的解析式分解为只有单个变换的函数链,然后依次进行单一变换,最终得到所要的函数图像.
第10讲 │ 要点探究
[答案] ①⑧⑤或①③⑧或④⑧①或④①⑧(填一组即可)
[思路] 先确定图像变换的种类,然后确定图像变换的顺序
第10讲 │ 要点探究
[点评] 将函数f(x)经过多种图像变换得到g(x)的图像,可能有多种不同的顺序,但不管按哪种顺序进行变换,都必须遵循“只能对函数关系式中的x、y进行变换”的原则,否则容易出错.
探究点4 函数图像的识别与应用
例4 如图10-5所示,一质点P(x,y)在xOy平面上沿曲线运动,速度大小不变,其在x轴上的影点Q(x,0)的运动速度V=V(t)的图像大致为( )
第10讲 │ 要点探究
图10-5
第10讲 │ 要点探究
[思路] 从已知图形中封闭曲线入手,研究投影点Q(x,0)的速度的变化规律.
[答案] B
[解析] 由图可知,当质点P(x,y)在两个封闭曲线上运动时,投影点Q(x,0)的速度先由正到0、到负数,到负数,再到0,到正,故A错误,质点P(x,y)在开始时沿直线运动,故投影点Q(x,0)的速度为常数,因此C是错误的,故选B.
[点评] 函数图像是函数关系的直观表现,它可以形象的反映函数中变量间的变化关系,有助于我们对函数关系的直观理解和对函数性质的分析,处理函数问题时要心中有形.
第10讲 │ 要点探究
[答案] C
(1)有四个函数:①y=x·sinx;②y=x·cosx;③y=x·|cosx|;④y=x·2x的图像(部分)如下,但顺序被打乱,则按照从左到右将图像对应的函数序号安排正确的一组是( )
A.④①②③ B.①④③②
C.①④②③ D.③④②①
图10-7
[解析] (1)函数xsinx是偶函数,因此其图像只能是第一个,函数y=xcosx与y=x|cosx|都为奇函数,但当x>0时,y=x|cosx|≥0恒成立,故函数只能是第四个,函数y=x·2x不具有奇偶性,因此其图像只能是第二个,故选C.
第10讲 │ 要点探究
(2)如图10-8,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图像大致是( )
图10-8
图10-9
[答案] B
第10讲 │ 要点探究
规律总结
第10讲 │ 规律总结
1.幂函数y=xa的图像一定会出现在第一象限内,一定不会出现的第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;在(0,1)上,幂函数中指数愈大,函数图像愈靠近x轴,在(1,+∞)上,幂函数中指数越大,函数图像越远离x轴;幂函数的单调性、奇偶性由指数决定.
2.作图
作图的常用方法有描点法和变换法,对前者,要注意对函数性质的研究;对后者,要熟悉常见函数及图像的变换法则,在解决函数图像的变换问题时,要遵循“只能对函数关系式中的x、y变换”的原则,写出每一次的变换所得图像对应的解析式,这样才能避免出错.
第10讲 │ 规律总结
3.识图
对于给定函数的图像,要能从图像的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等,注意图像与函数解析式中参数的关系.
4.用图
函数图像形象地显示了函数的性质,为研究数量关系提供了“形”的直观性,它是探求解题路径,获得问题结果的重要工具,要重视数形结合思想的应用.
