2012届高考复习方案数学理科(北师版)第1单元第1讲 集合及其运算
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第1单元第1讲 集合及其运算 |
|
|
| 格式 | rar | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第1讲 │ 集合及其运算
第1讲 集合及其运算
知识梳理
1.集合的含义与表示
(1)一般地,我们把研究对象统称为 ,把一些元素组成的总体叫做 (简称为集)。
(2)集合中的元素有三个性质:________,________,________。
(3)集合中元素与集合的关系分为________和________两种,分别用____和____表示。
(4)几个常用集合的表示法
第1讲 │ 知识梳理
元素
合集
确定性
互异性
无序性
数集 自然数集 正整数集 整数集 有理数集 实数集
表示法
属于
不属于
∈
N
N*或N+
Z
Q
R
(5)集合有三种表示法:________,________,__ ____。
列举法
描述法
Venn图法
第1讲 │ 知识梳理
2.集合间的基本关系
A B且A B
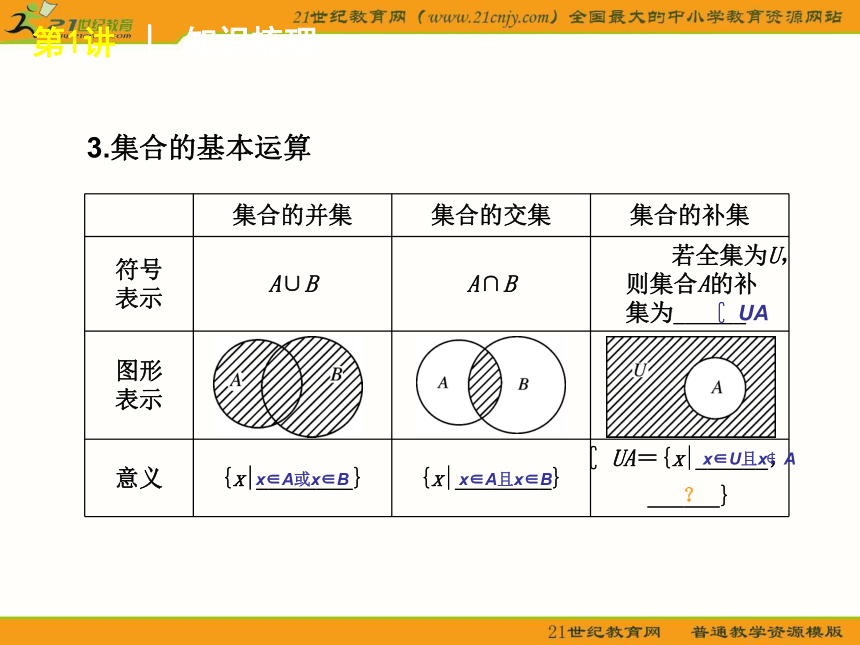
3.集合的基本运算
第1讲 │ 知识梳理
集合的并集 集合的交集 集合的补集
符号
表示 A∪B A∩B 若全集为U,则集合A的补集为______
图形
表示
意义 {x|________} {x|________} UA={x|______,______}
UA
x∈A或x∈B
x∈A且x∈B
x∈U且x A
?
4.常见结论
(1)若集合A中有n个元素,则集合A的子集有____个,真子集有______个。
(2)并集:A∪B=______,A∪A=___ _,A∪ =____,A∪B____A,A∪B=B A B。
(3)交集:A∩B=______,A∩A=____,A∩ =____,A∩B____A,A∩B=A A B。
(4)补集:A∩( UA)=____,A∪( UA)=____。
(5) U(A∪B)=________, U(A∩B)=_______。
(6)若A B且B A,则________。
第1讲 │ 知识梳理
2n
2n-1
B∪A
A
A
B∩A
A
U
UA ∩ U B
UA ∪ U B
A=B
要点探究
探究点1 集合的概念
第1讲 │ 要点探究
[思路] 由题意可知,集合A中的三个元素中必有一个为1,由此列出关于a的方程后求解,最后对结果进行检验.集合B为单元素集,要分a=0和a≠0两种情况讨论.
第1讲 │ 要点探究
探究点2 集合间的关系
例2 已知集合P={x|1+a≤x≤2-a},Q={x|x2-3x-10≤0}.
(1)若a=-3,求集合P,Q间的关系;
(2)若P Q,求实数a的取值范围.
第1讲 │ 要点探究
[思路] (1)求出集合Q,把a=-3代入集合P,利用数轴探讨P,Q间的包含或相等关系;(2)由P Q,注意集合P可为空集.
第1讲 │ 要点探究
第1讲 │ 要点探究
[点评] 由于空集是一个特殊的集合,它是任何集合的子集,因此利用A B解决问题时,要注意对集合A是否为空集进行讨论,解题时不要漏掉这一点;另外,合理利用数轴和Venn图帮助分析与求解是避免出错的一个有效手段,这也是数与形的完美结合之所在,如:
第1讲 │ 要点探究
(1)[2010·浙江卷] 设P={x<4},Q= {x2<4},则 ( )
A.P Q B.Q P
C.P RQ D.Q RP
[思路] 求出集合Q,利用数轴判断两个集合的相互关系
[解析] Q=(-2,2),P=(-∞,4),Q P.
第1讲 │ 要点探究
(2)[2010·宝鸡模拟] 已知全集U=R,集合A={x|x=2n,n∈N}与B={x|x=2n,n∈N},则正确表示集合A、B关系的韦恩(Venn)图是( )
[思路]将2n变形为2×2n-1的形式,再利用其判断集合A、B的关系
[解析] x=2n=2×2n-1,∴当n∈N+时,2n-1∈N+,此时A B,又1∈A,但1 B,故选A.
第1讲 │ 要点探究
(3)[2010·佛山模拟] 已知集合A={x|x>-2或x<-4},B={x|x2-4ax+3a2<0}.若B A,则实数a的取值范围是__________.
[思路] 先利用a的符号将集合B化简再分类讨论.
(-∞,-4]∪
第1讲 │ 要点探究
探究点3 集合的运算
例3 [2010·杭州模拟] 已知集合A= ,集合B= 。
(1)当m=3时,求A∩ ;
(2)若A∩B= ,求实数m的值。
第1讲 │ 要点探究
[思路] (1)集合A、B都表示函数的定义域,先利用使解析式有意义的条件求得集合A、B,然后借助数轴进行集合运算;(2)借助数轴,由集合的运算性质写出参数m所满足的条件即可求解.
第1讲 │ 要点探究
第1讲 │ 要点探究
(1)设U=Z,A={1,3,5,7,9},B={1,2,3,4,5},则图1-2中阴影部分表示的集合是( )
A.{2,4}
B.{1,2,3,4,5}
C.{7,9}
D.{1,3,5}
图1-2
[思路]根据给出的Venn图可知,所求的集合中的元素属于集合B但不属于集合A,即求 UA与B的交集
[解析]阴影部分所表示的集合是( UA)∩B={2,4},故选A.
第1讲 │ 要点探究
(2)若集合A= ,B= ,则A∩B是( )
A. B.
C. D.
[思路]利用不等式的解法,化简集合A,B,并利用数轴的直观性,计算两集合的交集.
第1讲 │ 要点探究
(3)[2010·重庆卷] 设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=____________.
[思路]集合A表示一元二次方程的根,根据这个方程的根是否相等分类解决,并注意对所求的结果进行检验
[解析]由x2+mx=0 x=0或x=-m,∴当m=0时A={0},不满足;当m≠0时,A={0,-m}.由 UA={1,2},∴-m=3,m=-3. .
探究点4 集合与其他知识的综合
例4 [2010·福建卷] 对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包含于Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如图1-3所示(阴影区域及其边界),其中为凸集的是__________.(写出所有凸集相应图形的序号)
第1讲 │ 要点探究
[答案] ②③
第1讲 │ 要点探究
[解析] 利用平面上的凸集的新定义知:连接Ω中任意两点的线段必定包含于Ω,那么对于①中多边形的最上面的两个角上相应的两点的连线就不包含于Ω,而对于④中分别在两个圆中各取一点的连线就不包含于Ω,对于②和③满足平面上的凸集的新定义.
[点评] 新型集合的概念及运算问题是近几年新课标高考的热点问题,解决此类信息迁移题的关键是在理解新信息并把它纳入已有的知识体系中,用原来的知识和方法来解决新情景下的问题,如:
第1讲 │ 要点探究
对任意两个集合M、N,定义:M-N={x|x∈M且x N},MΔN=(M-N)∪(N-M),M={y|y=x2,x∈R},N={y|y=3sinx,x∈R},则MΔN=________.
[解析] M=[0,+∞),N=[-3,3],∵M-N=,∴M-N=(3,+∞),N-M=[-3,0),又∵MΔN=(M-N)∪(N-M),∴MΔN=[-3,0)∪(3,+∞).
[答案] [-3,0)∪(3,+∞)
例5 集合A={(x,y)|y=a|x|},B={(x,y)|y=x+a},C=A∩B,且集合C为单元素集合,则实数a的取值范围为________.
第1讲 │ 要点探究
[思路] 集合A、B为点集,在平面直角坐标系中,作出两个函数的图像,利用数形结合思想求解.
第1讲 │ 要点探究
[点评] 集合作为工具经常渗透到函数、不等式、解析几何等知识中,解决此类问题时,要注意将集合语言转化为熟悉的数学语言,再求解.
规律总结
第1讲 │ 规律总结
1.集合的准确识别
对集合的准确识别,关键是要特别注意代表元素是什么,有什么属性,如果属性相同,但代表元素不同,所表示的集合也不一样,如集合{y|y=2x},{x|y=2x},{(x,y)|y=2x}表示不同的集合.
2.集合元素的性质
集合元素具有确定性、互异性、无序性三个特征,尤其是“互异性”在解题中要注意把握与运用,在解决元素含参数的集合问题时,千万别忘了检验,否则很可能会因为不满足“互异性”而导致结论错误.
第1讲 │ 规律总结
3.空集的特殊性
任何集合是它自身的子集,空集是任何集合的子集.在涉及集合之间的包含关系,利用A B解题时,若不明确集合A是否是为空集时,应对集合A的情况进行分类讨论,勿因忽略“空集是任何集合的子集”造成解题结果不全面.
4.数形结合思想的应用
在进行集合的运算时要尽可能地借助韦恩图和数轴使抽象问题直观化.一般地,集合元素离散时用韦恩图表示,集合元素连续时用数轴表示,用数轴表示时注意端点值的取舍.
第1讲 │ 规律总结
5.补集思想的应用
在解决集合有关问题时,如果从正面求解较困难,则采用“正难则反”的解题策略,具体地说,就是将研究对象的全体视为全集,求出使问题反面成立的集合A,则集合A的补集即为所求.
第1讲 │ 集合及其运算
第1讲 集合及其运算
知识梳理
1.集合的含义与表示
(1)一般地,我们把研究对象统称为 ,把一些元素组成的总体叫做 (简称为集)。
(2)集合中的元素有三个性质:________,________,________。
(3)集合中元素与集合的关系分为________和________两种,分别用____和____表示。
(4)几个常用集合的表示法
第1讲 │ 知识梳理
元素
合集
确定性
互异性
无序性
数集 自然数集 正整数集 整数集 有理数集 实数集
表示法
属于
不属于
∈
N
N*或N+
Z
Q
R
(5)集合有三种表示法:________,________,__ ____。
列举法
描述法
Venn图法
第1讲 │ 知识梳理
2.集合间的基本关系
A B且A B
3.集合的基本运算
第1讲 │ 知识梳理
集合的并集 集合的交集 集合的补集
符号
表示 A∪B A∩B 若全集为U,则集合A的补集为______
图形
表示
意义 {x|________} {x|________} UA={x|______,______}
UA
x∈A或x∈B
x∈A且x∈B
x∈U且x A
?
4.常见结论
(1)若集合A中有n个元素,则集合A的子集有____个,真子集有______个。
(2)并集:A∪B=______,A∪A=___ _,A∪ =____,A∪B____A,A∪B=B A B。
(3)交集:A∩B=______,A∩A=____,A∩ =____,A∩B____A,A∩B=A A B。
(4)补集:A∩( UA)=____,A∪( UA)=____。
(5) U(A∪B)=________, U(A∩B)=_______。
(6)若A B且B A,则________。
第1讲 │ 知识梳理
2n
2n-1
B∪A
A
A
B∩A
A
U
UA ∩ U B
UA ∪ U B
A=B
要点探究
探究点1 集合的概念
第1讲 │ 要点探究
[思路] 由题意可知,集合A中的三个元素中必有一个为1,由此列出关于a的方程后求解,最后对结果进行检验.集合B为单元素集,要分a=0和a≠0两种情况讨论.
第1讲 │ 要点探究
探究点2 集合间的关系
例2 已知集合P={x|1+a≤x≤2-a},Q={x|x2-3x-10≤0}.
(1)若a=-3,求集合P,Q间的关系;
(2)若P Q,求实数a的取值范围.
第1讲 │ 要点探究
[思路] (1)求出集合Q,把a=-3代入集合P,利用数轴探讨P,Q间的包含或相等关系;(2)由P Q,注意集合P可为空集.
第1讲 │ 要点探究
第1讲 │ 要点探究
[点评] 由于空集是一个特殊的集合,它是任何集合的子集,因此利用A B解决问题时,要注意对集合A是否为空集进行讨论,解题时不要漏掉这一点;另外,合理利用数轴和Venn图帮助分析与求解是避免出错的一个有效手段,这也是数与形的完美结合之所在,如:
第1讲 │ 要点探究
(1)[2010·浙江卷] 设P={x<4},Q= {x2<4},则 ( )
A.P Q B.Q P
C.P RQ D.Q RP
[思路] 求出集合Q,利用数轴判断两个集合的相互关系
[解析] Q=(-2,2),P=(-∞,4),Q P.
第1讲 │ 要点探究
(2)[2010·宝鸡模拟] 已知全集U=R,集合A={x|x=2n,n∈N}与B={x|x=2n,n∈N},则正确表示集合A、B关系的韦恩(Venn)图是( )
[思路]将2n变形为2×2n-1的形式,再利用其判断集合A、B的关系
[解析] x=2n=2×2n-1,∴当n∈N+时,2n-1∈N+,此时A B,又1∈A,但1 B,故选A.
第1讲 │ 要点探究
(3)[2010·佛山模拟] 已知集合A={x|x>-2或x<-4},B={x|x2-4ax+3a2<0}.若B A,则实数a的取值范围是__________.
[思路] 先利用a的符号将集合B化简再分类讨论.
(-∞,-4]∪
第1讲 │ 要点探究
探究点3 集合的运算
例3 [2010·杭州模拟] 已知集合A= ,集合B= 。
(1)当m=3时,求A∩ ;
(2)若A∩B= ,求实数m的值。
第1讲 │ 要点探究
[思路] (1)集合A、B都表示函数的定义域,先利用使解析式有意义的条件求得集合A、B,然后借助数轴进行集合运算;(2)借助数轴,由集合的运算性质写出参数m所满足的条件即可求解.
第1讲 │ 要点探究
第1讲 │ 要点探究
(1)设U=Z,A={1,3,5,7,9},B={1,2,3,4,5},则图1-2中阴影部分表示的集合是( )
A.{2,4}
B.{1,2,3,4,5}
C.{7,9}
D.{1,3,5}
图1-2
[思路]根据给出的Venn图可知,所求的集合中的元素属于集合B但不属于集合A,即求 UA与B的交集
[解析]阴影部分所表示的集合是( UA)∩B={2,4},故选A.
第1讲 │ 要点探究
(2)若集合A= ,B= ,则A∩B是( )
A. B.
C. D.
[思路]利用不等式的解法,化简集合A,B,并利用数轴的直观性,计算两集合的交集.
第1讲 │ 要点探究
(3)[2010·重庆卷] 设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=____________.
[思路]集合A表示一元二次方程的根,根据这个方程的根是否相等分类解决,并注意对所求的结果进行检验
[解析]由x2+mx=0 x=0或x=-m,∴当m=0时A={0},不满足;当m≠0时,A={0,-m}.由 UA={1,2},∴-m=3,m=-3. .
探究点4 集合与其他知识的综合
例4 [2010·福建卷] 对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包含于Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如图1-3所示(阴影区域及其边界),其中为凸集的是__________.(写出所有凸集相应图形的序号)
第1讲 │ 要点探究
[答案] ②③
第1讲 │ 要点探究
[解析] 利用平面上的凸集的新定义知:连接Ω中任意两点的线段必定包含于Ω,那么对于①中多边形的最上面的两个角上相应的两点的连线就不包含于Ω,而对于④中分别在两个圆中各取一点的连线就不包含于Ω,对于②和③满足平面上的凸集的新定义.
[点评] 新型集合的概念及运算问题是近几年新课标高考的热点问题,解决此类信息迁移题的关键是在理解新信息并把它纳入已有的知识体系中,用原来的知识和方法来解决新情景下的问题,如:
第1讲 │ 要点探究
对任意两个集合M、N,定义:M-N={x|x∈M且x N},MΔN=(M-N)∪(N-M),M={y|y=x2,x∈R},N={y|y=3sinx,x∈R},则MΔN=________.
[解析] M=[0,+∞),N=[-3,3],∵M-N=,∴M-N=(3,+∞),N-M=[-3,0),又∵MΔN=(M-N)∪(N-M),∴MΔN=[-3,0)∪(3,+∞).
[答案] [-3,0)∪(3,+∞)
例5 集合A={(x,y)|y=a|x|},B={(x,y)|y=x+a},C=A∩B,且集合C为单元素集合,则实数a的取值范围为________.
第1讲 │ 要点探究
[思路] 集合A、B为点集,在平面直角坐标系中,作出两个函数的图像,利用数形结合思想求解.
第1讲 │ 要点探究
[点评] 集合作为工具经常渗透到函数、不等式、解析几何等知识中,解决此类问题时,要注意将集合语言转化为熟悉的数学语言,再求解.
规律总结
第1讲 │ 规律总结
1.集合的准确识别
对集合的准确识别,关键是要特别注意代表元素是什么,有什么属性,如果属性相同,但代表元素不同,所表示的集合也不一样,如集合{y|y=2x},{x|y=2x},{(x,y)|y=2x}表示不同的集合.
2.集合元素的性质
集合元素具有确定性、互异性、无序性三个特征,尤其是“互异性”在解题中要注意把握与运用,在解决元素含参数的集合问题时,千万别忘了检验,否则很可能会因为不满足“互异性”而导致结论错误.
第1讲 │ 规律总结
3.空集的特殊性
任何集合是它自身的子集,空集是任何集合的子集.在涉及集合之间的包含关系,利用A B解题时,若不明确集合A是否是为空集时,应对集合A的情况进行分类讨论,勿因忽略“空集是任何集合的子集”造成解题结果不全面.
4.数形结合思想的应用
在进行集合的运算时要尽可能地借助韦恩图和数轴使抽象问题直观化.一般地,集合元素离散时用韦恩图表示,集合元素连续时用数轴表示,用数轴表示时注意端点值的取舍.
第1讲 │ 规律总结
5.补集思想的应用
在解决集合有关问题时,如果从正面求解较困难,则采用“正难则反”的解题策略,具体地说,就是将研究对象的全体视为全集,求出使问题反面成立的集合A,则集合A的补集即为所求.
同课章节目录
