2012届高考复习方案数学理科(北师版)第2单元第14讲 导数的应用
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第2单元第14讲 导数的应用 |
|
|
| 格式 | rar | ||
| 文件大小 | 224.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第14讲 │ 导数的应用
第14讲 导数的应用
知识梳理
1.函数的单调性
若函数f(x)在某区间内可导,则f′(x)>0 f(x)在该区间上____________;f′(x)<0 f(x)在该区间上____________.
反之,若f(x)在某区间上单调递增,则在该区间上有________恒成立;若f(x)在某区间上单调递减,则在该区间上有________恒成立.
2.函数的极值
(1)函数极值的定义
①已知函数y=f(x),设x0是定义域内任一点,如果对x0附近的所有点x,都有f(x)<f(x0),则称函数f(x)在点x0处取________,记作______________,并把x0称为函数f(x)的一个__________;
第14讲 │ 知识梳理
单调递减
单调递增
f′(x)≥0
f′(x)≤0
极大值
y最大值=f(x0)
极大值点
②如果在x0附近都有f(x)>f(x0),则称函数f(x)在点x0处取________,记作____________,并把x0称为函数f(x)的一个____________;
③极大值与极小值统称________,极大值点与极小值点统称为________.
(2)求函数极值的方法
①第1步:求导数f′(x);
②第2步:求方程f′(x)=0的所有实数根;
③第3步:当f(x0)=0时,如果在x0附近的左侧______,右侧________,那么f(x0)是极大值;如果在x0附近的左侧________,右侧________,那么f(x0)是极小值.
第14讲 │ 知识梳理
极小值
y最小值=f(x0)
极小值点
极值
极值点
f′(x)>0
f′(x)<0
f′(x)<0
f′(x)>0
第14讲 │ 知识梳理
3.函数的最值
(1)函数f(x)在[a,b]上必有最值的条件
如果在区间[a,b]上函数y=f(x)的图像________________________,那么它必有最大值和最小值.
(2)求函数y=f(x)在[a,b]上的最大值与最小值的步骤
①求函数y=f(x)在(a,b)内的______;
②将函数y=f(x)的各极值与__________________________比较,其中最大的一个是最大值,最小的一个是最小值.
4.f(x)>m恒成立等价于________;f(x)<m恒成立等价于________.
5.函数f(x)=ax3+bx2+cx+d(a≠0)有极大值为f(x1),极小值为f(x2),若函数有三个零点,则________________;函数有两个零点,则________________;函数有且仅有一个零点,则______________.
是一条连续不断的曲线
极值
端点处的函数值f(a)、f(b)
mm>f(x)max
f(x1)>0且f(x2)<0
f(x1)=0或f(x2)=0
f(x1)<0或f(x2)>0
要点探究
探究点1 利用导数研究函数的单调性
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
[点评] (1)利用导函数的性质比用函数单调性的定义要方便,它是根据导函数的正负性确定函数的单调性;(2)两个单调递增区间不能“并”起来.函数的单调性是函数在某一区间内的性质,讨论函数的单调性应在函数的定义域范围内进行.
第14讲 │ 要点探究
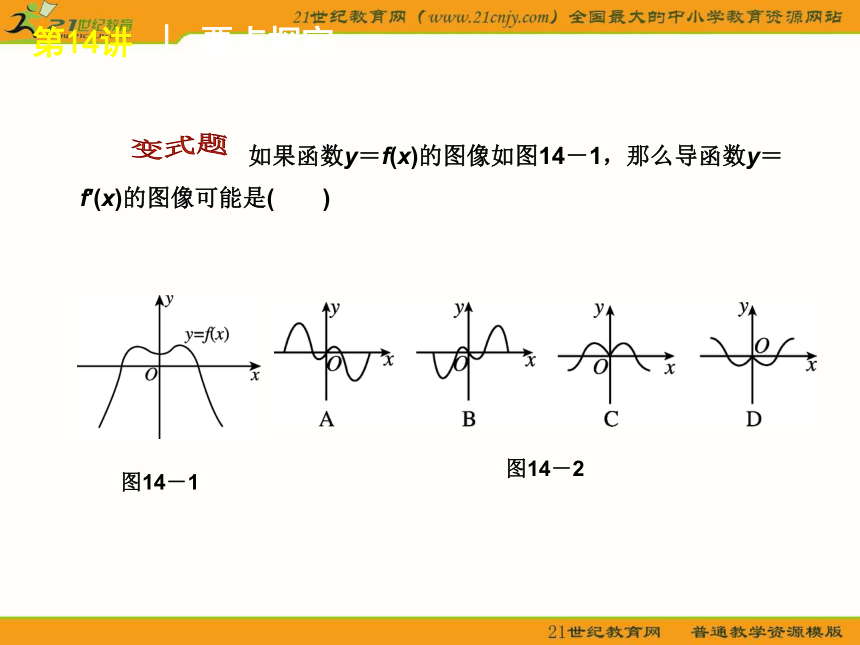
如果函数y=f(x)的图像如图14-1,那么导函数y=f′(x)的图像可能是( )
图14-1
图14-2
第14讲 │ 要点探究
[答案] A
[解析] 由原函数的单调性可以得到导函数的正负性情况,依次是“正、负、正、负”,即导函数的图像与x轴的位置应是“上、下、上、下”,符合规律的只有A
[思路] 由原函数的图像变化趋势是“增、减、增、减”,运用“增则正,减则负”规律,即可判断导函数的图像.
[点评] 解决此类问题时,审题应看清已知条件是导函数还是原函数,然后用“导数的正负性决定原函数的增减性”原则进行判断.
第14讲 │ 要点探究
已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围;
(3)是否存在a,使f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出a的值;若不存在,说明理由.
[思路] (1)通过解f′(x)>0求单调递增区间;(2)转化为f′(x)>0在R上恒成立问题,求a;(3)假设存在a,则f(0)是f(x)的极小值,或转化为恒成立问题.
第14讲 │ 要点探究
[解答] (1)f′(x)= ex-a.若a≤0,f′(x)=ex-a>0恒成立,即f(x)在R上递增.若a>0,ex-a≥0,∴ex≥a,x≥lna,∴f(x)的递增区间为(lna,+∞).
(2)∵f(x)在R内单调递增,∴f′(x)≥0在R上恒成立.∴ex-a≥0,即a≤ex在R上恒成立.∴a≤(ex)min,又∵ex>0,∴a≤0.
(3)方法一:由题意知ex-a≤0在(-∞,0]上恒成立.∴a≥ex在(-∞,0]上恒成立.∵ex在(-∞,0]上为增函数,∴x=0时,ex最大为1.∴a≥1,同理可知ex-a≥0在[0,+∞)上恒成立,∴a≤ex在[0,+∞)上恒成立,∴a≤1.
综上所述,a=1.
方法二:由题意知,x=0为f(x)的极小值点.∴f′(0)=0,即e0-a=0,∴a=1,经检验a=1符合题意.
第14讲 │ 要点探究
[点评] 已知函数f(x)在某区间内单调求参数问题,常转化为其导函数f′(x)在该区间内大于等于0(单调增函数)或小于等于0(单调减函数)恒成立问题.有时问题也可以借助集合的思想解决
探究点2 利用导数研究函数的极值与最值
第14讲 │ 要点探究
例2 已知a∈R,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数.
[解答] f′(x)=ex(x2+ax+a+1)+ex(2x+a)=ex[x2+(a+2)x+(2a+1)],
令f′(x)=0得x2+(a+2)x+(2a+1)=0.
(1)当Δ=(a+2)2-4(2a+1)=a2-4a=a(a-4)>0,
即a<0或a>4时x2+(a+2)x+(2a+1)=0有两个不同的实根x1,x2,不妨设x1于是f′(x)=ex(x-x1)(x-x2),从而有下表:
第14讲 │ 要点探究
即此时f(x)有两个极值点.
(2)当Δ=0即a=0或a=4时,方程x2+(a+2)x+(2a+1)=0有两个相同的实根x1=x2.于是f′(x)=ex(x-x1)2.故当x0,当x>x2时f′(x)>0,因此f(x)无极值.
(3)当Δ<0即00,
f′(x)=ex[x2+(a+2)x+(2a+1)]>0,故f(x)为增函数,此时f(x)无极值.因此当a>4或a<0时,f(x)有两个极值点,当0≤a≤4时,f(x)无极值点.
第14讲 │ 要点探究
例3 函数f(x)=ax3-6ax2+b在[-1,2]上的最大值为3,最小值为-29,求a,b的值
[解答] 由题设知a≠0,否则f(x)=b为常函数,与题设矛盾.f′(x)=3ax2-12ax=3ax(x-4),令f′(x)=0,得x1=0,x2=4(舍去).
①当a>0时,列表如下:
第14讲 │ 要点探究
由上表可知,当x=0时,f(x)取得极大值,也就是函数在[-1,2]上的最大值,∴f(0)=3,即b=3.又f(-1)=-7a+3,f(2)=-16a+3,f(2)②当a<0时,同理可得,当x=0时,f(x)取得极小值,也就是函数在[-1,2]上的最小值,∴f(0)=-29,即b=-29,又f(-1)=-7a-29,f(2)=-16a-29,f(2)>f(1),∴x=2时函数在[-1,2]上取得最大值,∴f(2)=-16a-29=3,∴a=-2.综上可得,a=2,b=3或a=-2,b=-29.
第14讲 │ 要点探究
[2010·宝鸡模拟] 已知函数f(x)=axlnx在点(e,f(e))处的切线与直线y=2x平行(其中e=2.71828…),g(x)=x2-tx-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[n,n+2](n>0)上的最小值;
(3)对一切x∈(0,e],3f(x)≥g(x)恒成立,求实数t的取值范围.
第14讲 │ 要点探究
第14讲 │ 要点探究
探究点3 导数在方程与不等式中的应用
例4 [2010·广州模拟] 已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值;
(2)求f(2)的取值范围;
(3)试探究直线y=x-1与函数y=f(x)的图像交点个数的情况,并说明理由.
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
探究点4 生活中的优化问题
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
[点评] 用导数求解实际问题中的最大值或最小值时,一般先设自变量、因变量,建立函数关系式,并确定其定义域,然后转化为导数模型求解.
规律总结
第14讲 │ 规律总结
1.函数的单调性、极值、最值都是定义域内的局部性质,因此利用导数讨论函数的性质时,首先要研究函数的定义域,再利用导数f′(x)解决.
2.通过判断函数各区间内导数f′(x)的符号,可判断函数f(x)在该区间上的单调性.若f′>0(或f′<0),则函数f在相应区间上是增加(或减少)的.
3.根据极值的定义,导数为0且在该点两侧导数的符号相反,则该点是函数的极值点.利用导数求函数的极值时,通过导数为零的点将整个定义域分为若干个区间,然后将x,f′(x),f在每个区间内的变化情况列在一个表格中,通过表格可以清楚地判断在哪个点处取得极值,是极大值还是极小值,所以在解题中注意表格的正确列法.
第14讲 │ 规律总结
4.根据最值的定义可知:函数的最值只可能在极值点取得,或者在区间的端点处取得.因此,求函数在闭区间内的最值时,只需要比较导数为0的点的函数值与端点值的大小,其中最大的值即为函数的最大值,最小的值即为函数的最小值.
第14讲 │ 规律总结
5.导数是解决生产生活中最优化问题的通性通法,利用导数求实际问题的最值的一般步骤和方法如下:(1)细致分析实际问题中各个量之间的关系,正确设定所求最大值或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),并根据实际问题中的限制条件确定y=f(x)的定义域;(2)求f′(x),令f′(x)=0,得出方程所有实数根;(3)比较函数在各个区间端点和在极值点的取值大小,确定其为最大值还是最小值;(4)检验结果的实际意义,给出答案.
第14讲 │ 规律总结
6.利用导数证明不等式是导数的应用之一,一般地,要证明不等式f(x)>g(x)在区间I上恒成立,则可构造函数h(x)=f(x)-g(x),通过讨论h′(x)在区间I上的取值范围,判断出函数h(x)的单调性,然后由函数h(x)在区间I上的一个初始值,证得不等式成立;利用导数研究方程问题,主要是指根据方程构造函数,然后利用导数,研究得到函数的单调性、极值、最值,从而结合函数图像来研究方程的根的个数、大小等问题.
第14讲 │ 导数的应用
第14讲 导数的应用
知识梳理
1.函数的单调性
若函数f(x)在某区间内可导,则f′(x)>0 f(x)在该区间上____________;f′(x)<0 f(x)在该区间上____________.
反之,若f(x)在某区间上单调递增,则在该区间上有________恒成立;若f(x)在某区间上单调递减,则在该区间上有________恒成立.
2.函数的极值
(1)函数极值的定义
①已知函数y=f(x),设x0是定义域内任一点,如果对x0附近的所有点x,都有f(x)<f(x0),则称函数f(x)在点x0处取________,记作______________,并把x0称为函数f(x)的一个__________;
第14讲 │ 知识梳理
单调递减
单调递增
f′(x)≥0
f′(x)≤0
极大值
y最大值=f(x0)
极大值点
②如果在x0附近都有f(x)>f(x0),则称函数f(x)在点x0处取________,记作____________,并把x0称为函数f(x)的一个____________;
③极大值与极小值统称________,极大值点与极小值点统称为________.
(2)求函数极值的方法
①第1步:求导数f′(x);
②第2步:求方程f′(x)=0的所有实数根;
③第3步:当f(x0)=0时,如果在x0附近的左侧______,右侧________,那么f(x0)是极大值;如果在x0附近的左侧________,右侧________,那么f(x0)是极小值.
第14讲 │ 知识梳理
极小值
y最小值=f(x0)
极小值点
极值
极值点
f′(x)>0
f′(x)<0
f′(x)<0
f′(x)>0
第14讲 │ 知识梳理
3.函数的最值
(1)函数f(x)在[a,b]上必有最值的条件
如果在区间[a,b]上函数y=f(x)的图像________________________,那么它必有最大值和最小值.
(2)求函数y=f(x)在[a,b]上的最大值与最小值的步骤
①求函数y=f(x)在(a,b)内的______;
②将函数y=f(x)的各极值与__________________________比较,其中最大的一个是最大值,最小的一个是最小值.
4.f(x)>m恒成立等价于________;f(x)<m恒成立等价于________.
5.函数f(x)=ax3+bx2+cx+d(a≠0)有极大值为f(x1),极小值为f(x2),若函数有三个零点,则________________;函数有两个零点,则________________;函数有且仅有一个零点,则______________.
是一条连续不断的曲线
极值
端点处的函数值f(a)、f(b)
m
f(x1)>0且f(x2)<0
f(x1)=0或f(x2)=0
f(x1)<0或f(x2)>0
要点探究
探究点1 利用导数研究函数的单调性
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
[点评] (1)利用导函数的性质比用函数单调性的定义要方便,它是根据导函数的正负性确定函数的单调性;(2)两个单调递增区间不能“并”起来.函数的单调性是函数在某一区间内的性质,讨论函数的单调性应在函数的定义域范围内进行.
第14讲 │ 要点探究
如果函数y=f(x)的图像如图14-1,那么导函数y=f′(x)的图像可能是( )
图14-1
图14-2
第14讲 │ 要点探究
[答案] A
[解析] 由原函数的单调性可以得到导函数的正负性情况,依次是“正、负、正、负”,即导函数的图像与x轴的位置应是“上、下、上、下”,符合规律的只有A
[思路] 由原函数的图像变化趋势是“增、减、增、减”,运用“增则正,减则负”规律,即可判断导函数的图像.
[点评] 解决此类问题时,审题应看清已知条件是导函数还是原函数,然后用“导数的正负性决定原函数的增减性”原则进行判断.
第14讲 │ 要点探究
已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围;
(3)是否存在a,使f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出a的值;若不存在,说明理由.
[思路] (1)通过解f′(x)>0求单调递增区间;(2)转化为f′(x)>0在R上恒成立问题,求a;(3)假设存在a,则f(0)是f(x)的极小值,或转化为恒成立问题.
第14讲 │ 要点探究
[解答] (1)f′(x)= ex-a.若a≤0,f′(x)=ex-a>0恒成立,即f(x)在R上递增.若a>0,ex-a≥0,∴ex≥a,x≥lna,∴f(x)的递增区间为(lna,+∞).
(2)∵f(x)在R内单调递增,∴f′(x)≥0在R上恒成立.∴ex-a≥0,即a≤ex在R上恒成立.∴a≤(ex)min,又∵ex>0,∴a≤0.
(3)方法一:由题意知ex-a≤0在(-∞,0]上恒成立.∴a≥ex在(-∞,0]上恒成立.∵ex在(-∞,0]上为增函数,∴x=0时,ex最大为1.∴a≥1,同理可知ex-a≥0在[0,+∞)上恒成立,∴a≤ex在[0,+∞)上恒成立,∴a≤1.
综上所述,a=1.
方法二:由题意知,x=0为f(x)的极小值点.∴f′(0)=0,即e0-a=0,∴a=1,经检验a=1符合题意.
第14讲 │ 要点探究
[点评] 已知函数f(x)在某区间内单调求参数问题,常转化为其导函数f′(x)在该区间内大于等于0(单调增函数)或小于等于0(单调减函数)恒成立问题.有时问题也可以借助集合的思想解决
探究点2 利用导数研究函数的极值与最值
第14讲 │ 要点探究
例2 已知a∈R,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数.
[解答] f′(x)=ex(x2+ax+a+1)+ex(2x+a)=ex[x2+(a+2)x+(2a+1)],
令f′(x)=0得x2+(a+2)x+(2a+1)=0.
(1)当Δ=(a+2)2-4(2a+1)=a2-4a=a(a-4)>0,
即a<0或a>4时x2+(a+2)x+(2a+1)=0有两个不同的实根x1,x2,不妨设x1
第14讲 │ 要点探究
即此时f(x)有两个极值点.
(2)当Δ=0即a=0或a=4时,方程x2+(a+2)x+(2a+1)=0有两个相同的实根x1=x2.于是f′(x)=ex(x-x1)2.故当x
(3)当Δ<0即0
f′(x)=ex[x2+(a+2)x+(2a+1)]>0,故f(x)为增函数,此时f(x)无极值.因此当a>4或a<0时,f(x)有两个极值点,当0≤a≤4时,f(x)无极值点.
第14讲 │ 要点探究
例3 函数f(x)=ax3-6ax2+b在[-1,2]上的最大值为3,最小值为-29,求a,b的值
[解答] 由题设知a≠0,否则f(x)=b为常函数,与题设矛盾.f′(x)=3ax2-12ax=3ax(x-4),令f′(x)=0,得x1=0,x2=4(舍去).
①当a>0时,列表如下:
第14讲 │ 要点探究
由上表可知,当x=0时,f(x)取得极大值,也就是函数在[-1,2]上的最大值,∴f(0)=3,即b=3.又f(-1)=-7a+3,f(2)=-16a+3,f(2)
第14讲 │ 要点探究
[2010·宝鸡模拟] 已知函数f(x)=axlnx在点(e,f(e))处的切线与直线y=2x平行(其中e=2.71828…),g(x)=x2-tx-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[n,n+2](n>0)上的最小值;
(3)对一切x∈(0,e],3f(x)≥g(x)恒成立,求实数t的取值范围.
第14讲 │ 要点探究
第14讲 │ 要点探究
探究点3 导数在方程与不等式中的应用
例4 [2010·广州模拟] 已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值;
(2)求f(2)的取值范围;
(3)试探究直线y=x-1与函数y=f(x)的图像交点个数的情况,并说明理由.
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
探究点4 生活中的优化问题
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
第14讲 │ 要点探究
[点评] 用导数求解实际问题中的最大值或最小值时,一般先设自变量、因变量,建立函数关系式,并确定其定义域,然后转化为导数模型求解.
规律总结
第14讲 │ 规律总结
1.函数的单调性、极值、最值都是定义域内的局部性质,因此利用导数讨论函数的性质时,首先要研究函数的定义域,再利用导数f′(x)解决.
2.通过判断函数各区间内导数f′(x)的符号,可判断函数f(x)在该区间上的单调性.若f′>0(或f′<0),则函数f在相应区间上是增加(或减少)的.
3.根据极值的定义,导数为0且在该点两侧导数的符号相反,则该点是函数的极值点.利用导数求函数的极值时,通过导数为零的点将整个定义域分为若干个区间,然后将x,f′(x),f在每个区间内的变化情况列在一个表格中,通过表格可以清楚地判断在哪个点处取得极值,是极大值还是极小值,所以在解题中注意表格的正确列法.
第14讲 │ 规律总结
4.根据最值的定义可知:函数的最值只可能在极值点取得,或者在区间的端点处取得.因此,求函数在闭区间内的最值时,只需要比较导数为0的点的函数值与端点值的大小,其中最大的值即为函数的最大值,最小的值即为函数的最小值.
第14讲 │ 规律总结
5.导数是解决生产生活中最优化问题的通性通法,利用导数求实际问题的最值的一般步骤和方法如下:(1)细致分析实际问题中各个量之间的关系,正确设定所求最大值或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),并根据实际问题中的限制条件确定y=f(x)的定义域;(2)求f′(x),令f′(x)=0,得出方程所有实数根;(3)比较函数在各个区间端点和在极值点的取值大小,确定其为最大值还是最小值;(4)检验结果的实际意义,给出答案.
第14讲 │ 规律总结
6.利用导数证明不等式是导数的应用之一,一般地,要证明不等式f(x)>g(x)在区间I上恒成立,则可构造函数h(x)=f(x)-g(x),通过讨论h′(x)在区间I上的取值范围,判断出函数h(x)的单调性,然后由函数h(x)在区间I上的一个初始值,证得不等式成立;利用导数研究方程问题,主要是指根据方程构造函数,然后利用导数,研究得到函数的单调性、极值、最值,从而结合函数图像来研究方程的根的个数、大小等问题.
同课章节目录
