2012届高考复习方案数学理科(北师版)第3单元第18讲 三角函数的图像和性质
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第3单元第18讲 三角函数的图像和性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 355.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
第18讲 │ 三角函数的图像和性质
第18讲 三角函数的图像和性质
知识梳理
1.周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有____ ____,那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小正数,那么这个最小正数就叫做f(x)的最小正周期.
第18讲 │ 知识梳理
f(x+T)=f(x)
2.五点法作图原理
在确定正弦函数y=sinx,x∈[0,2π]的图象形状时,起关键作用的五点是___________________________________________________.
在确定余弦函数y=cosx,x∈[0,2π]的图象形状时,起关键作用的五点是__________________________________________________.
第18讲 │ 知识梳理
第18讲 │ 知识梳理
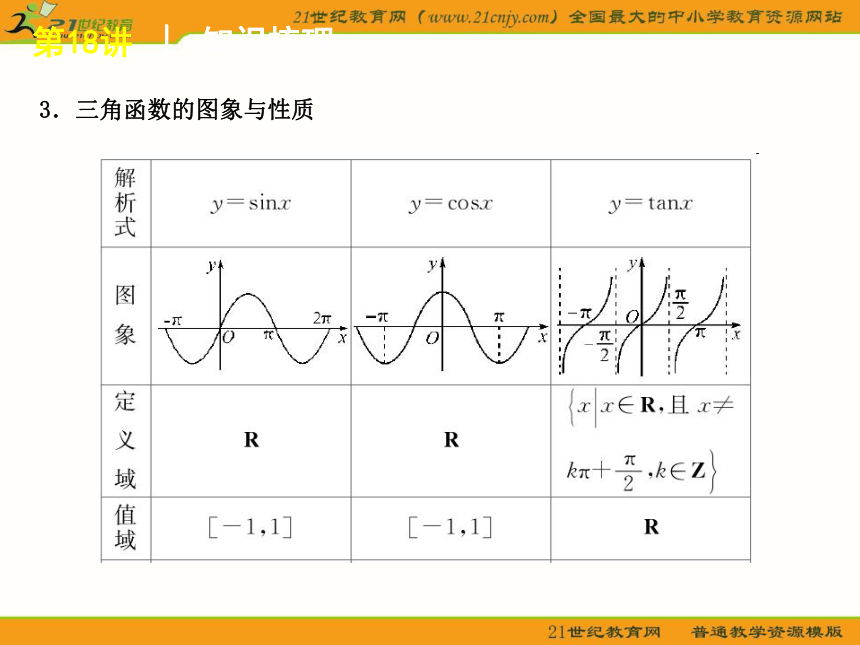
3.三角函数的图象与性质
第18讲 │ 知识梳理
2π
2π
π
奇
偶
奇
第18讲 │ 知识梳理
增
减
增
减
增
第18讲 │ 知识梳理
4.三角函数图象的对称性:
(1)正弦函数y=sinx图象的对称中心是(kπ,0)(k∈Z),对称轴方程是_______ _____;
(2)余弦函数y=cosx图象的对称中心是____ _______,对称轴方程是x=kπ(k∈Z);
(3)正切函数y=tanx图象的对称中心是______________,不存在对称轴.
要点探究
探究点1 三角函数图像的简单应用
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 根据三角函数的图象,从数形结合的角度求解一些基本的三角函数不等式的解、判断函数图象的对称性等,要准确使用图象进行观察分析.在以函数图象为切入点的试题中要注意画图的准确性,注意借助于数的演算对图形问题给出定量结果.在函数图象分析类试题中,数的佐证是必不可少的,如下面的变式.
第18讲 │ 要点探究
函数y=-xcosx的部分图象是( )
[思路] 根据函数的解析式检验函数的奇偶性以及函数值的变化趋势,以数助形解决问题.
[答案] D
第18讲 │ 要点探究
探究点2 三角函数的值域与最值
第18讲 │ 要点探究
第18讲 │ 要点探究
[思路] (1)是关于正弦函数的二次式;(2)可以根据同角三角函数关系化为正弦函数的二次式,根据正弦函数的有界性通过配方求解.
第18讲 │ 要点探究
[答案] (1)C (2)D
第18讲 │ 要点探究
第18讲 │ 要点探究
[答案] A
[思路] 函数式展开后将出现sinxcosx和sinx+cosx,可以用sinx+cosx表示sinxcosx后换元解决.
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 在三角函数问题中,(sinx±cosx)2=1±2sinxcosx=1±sin2x是一个很重要的公式,它是联系sinx±cosx和sinxcosx关系的纽带,许多与此相关的问题就是通过这个公式实现问题转化的.
探究点3 三角函数的奇偶性与周期性
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[答案] (1)B (2)B
[思路] (1)根据周期性和奇偶性把所求的函数值转化到已知区间上的函数值;(2)根据函数是偶函数,利用偶函数的性质.
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 函数的奇偶性反映了函数在关于定义域对称区间上函数值的规律,利用这个规律可以由一个函数值求解另外一个函数值,其功能之一就是转化函数值到已知;函数的周期性反映了在等距离(周期的倍数)上的两个函数值之间的相等关系,其功能也是把函数值进行转化,以达到由已知函数值求解未知函数值的目的.特别指出对偶函数而言f(x)=f(|x|).函数奇偶性是函数的整体性质,奇偶性定义是解题的基本依据,看下面的变式.
第18讲 │ 要点探究
[答案] D
[思路] 根据函数是奇函数必须满足f(-x)=-f(x),得到关于x的恒等式,根据这个等式恒成立的条件确定φ所满足的关系,或者根据定义在R上的奇函数必须满足f(0)=0求解.
第18讲 │ 要点探究
探究点4 三角函数的单调性
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[思路] (1)根据角A,B之和小于,利用正弦函数或者余弦函数的单调性确定A,B的正弦和余弦的大小,再根据函数f(x)的单调性进行判断;(2)把x+看做一个整体,根据正切函数的单调性求解.
[答案] (1)C (2)C
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 三角函数的单调性反映了具有大小关系的两个角之间三角函数值的大小,利用三角函数的单调性比较三角函数值的大小是单调性的主要应用之一.较为简单的函数y=tan(x+φ)的单调区间可以把x+φ看成一个整体,利用正切函数得到其单调区间,高考重点考查y=Asin(ωx+φ)的图象和性质(在第21讲重点解决这个问题),对正切的情况要求不高,复习时点到为止.
第18讲 │ 要点探究
[思路] (1)根据函数性质把函数变换为y=-sin后解决;(2)结合函数的图象变换方法和余弦函数的单调性解决.
第18讲 │ 要点探究
第18讲 │ 要点探究
规律总结
第18讲 │ 规律总结
1.三角函数的图象从形上完全反映了三角函数的性质,要善于从图象上记忆三角函数的性质,注意根据三角函数图象分析解决问题.
2.在三角函数中正弦、余弦函数是有界的,正弦、余弦函数的有界性在求函数值域或最值中发挥着重要作用.
3.函数的周期性是函数在定义域上的整体性质,即对定义域上的任意自变量都满足f(x+T)=f(x),这个性质的主要作用是化简三角函数式和把未知的三角函数值转化为已知的三角函数值.
第18讲 │ 规律总结
4.三角函数的单调性是函数的局部性质,三角函数的单调区间都是对同一个k值而言的,在同一个k值的区间上三角函数是单调的,在这个区间上可以根据单调性确定具有大小关系的两个自变量的函数值的大小,在k值不同的区间上,三角函数是不单调的.
第18讲 │ 三角函数的图像和性质
第18讲 三角函数的图像和性质
知识梳理
1.周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有____ ____,那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小正数,那么这个最小正数就叫做f(x)的最小正周期.
第18讲 │ 知识梳理
f(x+T)=f(x)
2.五点法作图原理
在确定正弦函数y=sinx,x∈[0,2π]的图象形状时,起关键作用的五点是___________________________________________________.
在确定余弦函数y=cosx,x∈[0,2π]的图象形状时,起关键作用的五点是__________________________________________________.
第18讲 │ 知识梳理
第18讲 │ 知识梳理
3.三角函数的图象与性质
第18讲 │ 知识梳理
2π
2π
π
奇
偶
奇
第18讲 │ 知识梳理
增
减
增
减
增
第18讲 │ 知识梳理
4.三角函数图象的对称性:
(1)正弦函数y=sinx图象的对称中心是(kπ,0)(k∈Z),对称轴方程是_______ _____;
(2)余弦函数y=cosx图象的对称中心是____ _______,对称轴方程是x=kπ(k∈Z);
(3)正切函数y=tanx图象的对称中心是______________,不存在对称轴.
要点探究
探究点1 三角函数图像的简单应用
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 根据三角函数的图象,从数形结合的角度求解一些基本的三角函数不等式的解、判断函数图象的对称性等,要准确使用图象进行观察分析.在以函数图象为切入点的试题中要注意画图的准确性,注意借助于数的演算对图形问题给出定量结果.在函数图象分析类试题中,数的佐证是必不可少的,如下面的变式.
第18讲 │ 要点探究
函数y=-xcosx的部分图象是( )
[思路] 根据函数的解析式检验函数的奇偶性以及函数值的变化趋势,以数助形解决问题.
[答案] D
第18讲 │ 要点探究
探究点2 三角函数的值域与最值
第18讲 │ 要点探究
第18讲 │ 要点探究
[思路] (1)是关于正弦函数的二次式;(2)可以根据同角三角函数关系化为正弦函数的二次式,根据正弦函数的有界性通过配方求解.
第18讲 │ 要点探究
[答案] (1)C (2)D
第18讲 │ 要点探究
第18讲 │ 要点探究
[答案] A
[思路] 函数式展开后将出现sinxcosx和sinx+cosx,可以用sinx+cosx表示sinxcosx后换元解决.
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 在三角函数问题中,(sinx±cosx)2=1±2sinxcosx=1±sin2x是一个很重要的公式,它是联系sinx±cosx和sinxcosx关系的纽带,许多与此相关的问题就是通过这个公式实现问题转化的.
探究点3 三角函数的奇偶性与周期性
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[答案] (1)B (2)B
[思路] (1)根据周期性和奇偶性把所求的函数值转化到已知区间上的函数值;(2)根据函数是偶函数,利用偶函数的性质.
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 函数的奇偶性反映了函数在关于定义域对称区间上函数值的规律,利用这个规律可以由一个函数值求解另外一个函数值,其功能之一就是转化函数值到已知;函数的周期性反映了在等距离(周期的倍数)上的两个函数值之间的相等关系,其功能也是把函数值进行转化,以达到由已知函数值求解未知函数值的目的.特别指出对偶函数而言f(x)=f(|x|).函数奇偶性是函数的整体性质,奇偶性定义是解题的基本依据,看下面的变式.
第18讲 │ 要点探究
[答案] D
[思路] 根据函数是奇函数必须满足f(-x)=-f(x),得到关于x的恒等式,根据这个等式恒成立的条件确定φ所满足的关系,或者根据定义在R上的奇函数必须满足f(0)=0求解.
第18讲 │ 要点探究
探究点4 三角函数的单调性
第18讲 │ 要点探究
第18讲 │ 要点探究
第18讲 │ 要点探究
[思路] (1)根据角A,B之和小于,利用正弦函数或者余弦函数的单调性确定A,B的正弦和余弦的大小,再根据函数f(x)的单调性进行判断;(2)把x+看做一个整体,根据正切函数的单调性求解.
[答案] (1)C (2)C
第18讲 │ 要点探究
第18讲 │ 要点探究
[点评] 三角函数的单调性反映了具有大小关系的两个角之间三角函数值的大小,利用三角函数的单调性比较三角函数值的大小是单调性的主要应用之一.较为简单的函数y=tan(x+φ)的单调区间可以把x+φ看成一个整体,利用正切函数得到其单调区间,高考重点考查y=Asin(ωx+φ)的图象和性质(在第21讲重点解决这个问题),对正切的情况要求不高,复习时点到为止.
第18讲 │ 要点探究
[思路] (1)根据函数性质把函数变换为y=-sin后解决;(2)结合函数的图象变换方法和余弦函数的单调性解决.
第18讲 │ 要点探究
第18讲 │ 要点探究
规律总结
第18讲 │ 规律总结
1.三角函数的图象从形上完全反映了三角函数的性质,要善于从图象上记忆三角函数的性质,注意根据三角函数图象分析解决问题.
2.在三角函数中正弦、余弦函数是有界的,正弦、余弦函数的有界性在求函数值域或最值中发挥着重要作用.
3.函数的周期性是函数在定义域上的整体性质,即对定义域上的任意自变量都满足f(x+T)=f(x),这个性质的主要作用是化简三角函数式和把未知的三角函数值转化为已知的三角函数值.
第18讲 │ 规律总结
4.三角函数的单调性是函数的局部性质,三角函数的单调区间都是对同一个k值而言的,在同一个k值的区间上三角函数是单调的,在这个区间上可以根据单调性确定具有大小关系的两个自变量的函数值的大小,在k值不同的区间上,三角函数是不单调的.
