2012届高考复习方案数学理科(北师版)第3单元第23讲 解三角形的应用
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第3单元第23讲 解三角形的应用 |
|
|
| 格式 | rar | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 18:07:35 | ||
图片预览








文档简介
(共33张PPT)
第23讲 │ 解三角形的应用
第23讲 解三角形的应用
知识梳理
第23讲 │ 知识梳理
α+β+∠B=π
2RsinB
2RsinC
第23讲 │ 知识梳理
正弦
正弦
余弦
第23讲 │ 知识梳理
atanα
ADsinβ
3.实际问题中常用的角
(1)仰角和俯角
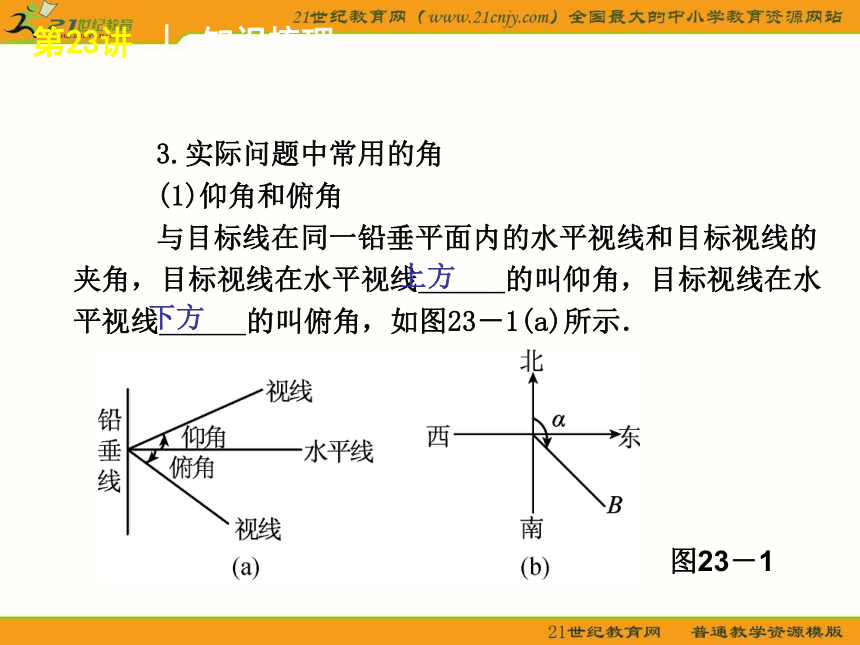
与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线______的叫仰角,目标视线在水平视线______的叫俯角,如图23-1(a)所示.
第23讲 │ 知识梳理
上方
下方
图23-1
第23讲 │ 知识梳理
正北
(2)方位角
指从某点的________方向顺时针转到目标方向线的水平角,如图23-1(b)中B点的方位角为α.
(3)坡度:坡面与水平面所成的二面角的度数.
第23讲 │ 知识梳理
第23讲 │ 知识梳理
-cosC
-tan(A+B)
要点探究
探究点1 距离的测量
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
[思路] 要求出M,N间距离,可以以MN为边构造三角形,把问题转化为解三角形问题.首先要寻找已知条件,这里可借助于可测的A点到M,N点的俯角及B点到M,N的俯角以及A,B间的距离.
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
[点评] 测量问题的关键是把测量目标纳入到一个可解三角形中,三角形可解,则至少要知道这个三角形的一条边长.本题中把测量目标纳入到△AMN或者△BMN均可,这两个三角形只能测量出求解目标的对角,要解这样的三角形就必需求出其中的两条边长,而这两条边长就可以借助于△MAB,△NAB求出.根据求解目标确定三角形,借助于其他的三角形求这个三角形的元素,就是测量问题的基本思想.请看下面的变式.
第23讲 │ 要点探究
[2010·陕西卷] 如图23-3所示,A,B是海面上位于东西方向相距5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
图23-3
第23讲 │ 要点探究
[思路] 求解的目标是CD的长度,根据已知△DAB可解,在△DBC中,可以求出BD,又已知BC和∠CBD,根据余弦定理即可求出CD.
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点2 高度的测量
第23讲 │ 要点探究
图23-4
第23讲 │ 要点探究
[思路] 不可到达底部的测高问题,可考虑解高所在的直角三角形和水平的斜三角形.
第23讲 │ 要点探究
[思路] 根据题意画出解题示意图,根据立体几何知识和解三角形的方法解决.
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点3 三角形的面积
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点4 三角形中边角问题的综合
第23讲 │ 要点探究
第23讲 │ 要点探究
[思路] (1)三角形的两条边所在向量的数量积实际是这两条边的边长与其夹角的余弦之间的关系,转化后,再根据正弦定理把边的关系转化为角的关系,即可求出角B;(2)所求的数量积中两向量的夹角是已知的,两向量的模之间可以根据余弦定理建立一个等式,只要根据基本不等式即可求出模的乘积的最小值.
第23讲 │ 要点探究
第23讲 │ 要点探究
[点评] 根据正弦定理和余弦定理,实现三角形之间关系的相互转化,然后根据转化后的方程求解三角形的元素是解三角形的基本方法.当三角形中的已知元素不能完全把三角形固定下来时,可以根据正弦定理和余弦定理建立其三角之间的关系,通过这个关系式达到求解最值、范围之类的问题.
规律总结
第23讲 │ 规律总结
1.解决测量问题的基本方法是把测量目标纳入到一个三角形中,这个三角形的一些元素是可以测量出来的,一些元素是可以借助于其他可以测量的三角形求解出来的,通过测量的、求解的元素使这个三角形可解.
2.解决不可及目标的测量、航海问题的计算,要注意各种角的概念,解题时根据这些概念画出图形,然后分析求解目标所在的三角形,在整体中寻找这个三角形可解的条件,然后制订计划具体求解各个三角形.
第23讲 │ 规律总结
第23讲 │ 解三角形的应用
第23讲 解三角形的应用
知识梳理
第23讲 │ 知识梳理
α+β+∠B=π
2RsinB
2RsinC
第23讲 │ 知识梳理
正弦
正弦
余弦
第23讲 │ 知识梳理
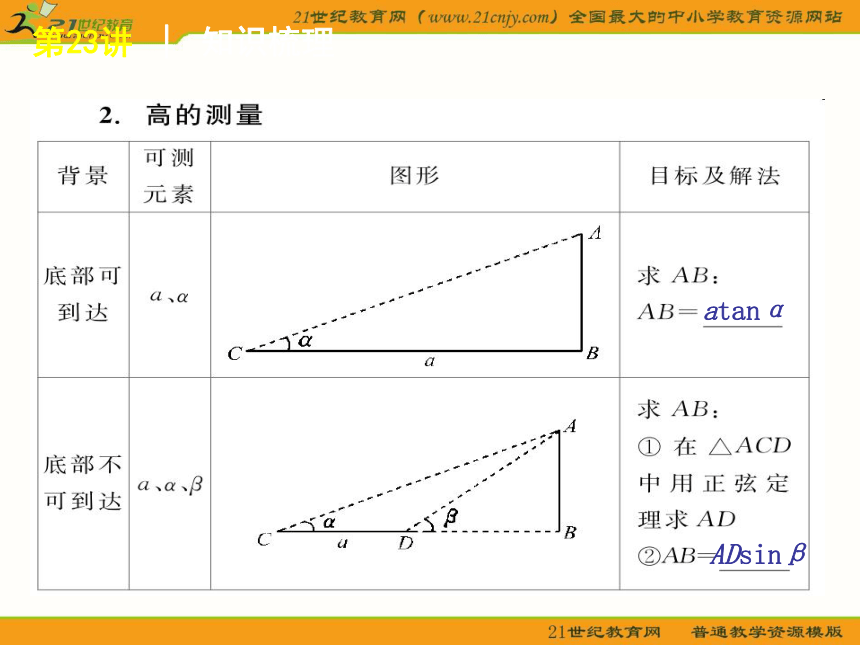
atanα
ADsinβ
3.实际问题中常用的角
(1)仰角和俯角
与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线______的叫仰角,目标视线在水平视线______的叫俯角,如图23-1(a)所示.
第23讲 │ 知识梳理
上方
下方
图23-1
第23讲 │ 知识梳理
正北
(2)方位角
指从某点的________方向顺时针转到目标方向线的水平角,如图23-1(b)中B点的方位角为α.
(3)坡度:坡面与水平面所成的二面角的度数.
第23讲 │ 知识梳理
第23讲 │ 知识梳理
-cosC
-tan(A+B)
要点探究
探究点1 距离的测量
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
[思路] 要求出M,N间距离,可以以MN为边构造三角形,把问题转化为解三角形问题.首先要寻找已知条件,这里可借助于可测的A点到M,N点的俯角及B点到M,N的俯角以及A,B间的距离.
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
[点评] 测量问题的关键是把测量目标纳入到一个可解三角形中,三角形可解,则至少要知道这个三角形的一条边长.本题中把测量目标纳入到△AMN或者△BMN均可,这两个三角形只能测量出求解目标的对角,要解这样的三角形就必需求出其中的两条边长,而这两条边长就可以借助于△MAB,△NAB求出.根据求解目标确定三角形,借助于其他的三角形求这个三角形的元素,就是测量问题的基本思想.请看下面的变式.
第23讲 │ 要点探究
[2010·陕西卷] 如图23-3所示,A,B是海面上位于东西方向相距5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
图23-3
第23讲 │ 要点探究
[思路] 求解的目标是CD的长度,根据已知△DAB可解,在△DBC中,可以求出BD,又已知BC和∠CBD,根据余弦定理即可求出CD.
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点2 高度的测量
第23讲 │ 要点探究
图23-4
第23讲 │ 要点探究
[思路] 不可到达底部的测高问题,可考虑解高所在的直角三角形和水平的斜三角形.
第23讲 │ 要点探究
[思路] 根据题意画出解题示意图,根据立体几何知识和解三角形的方法解决.
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点3 三角形的面积
第23讲 │ 要点探究
第23讲 │ 要点探究
第23讲 │ 要点探究
探究点4 三角形中边角问题的综合
第23讲 │ 要点探究
第23讲 │ 要点探究
[思路] (1)三角形的两条边所在向量的数量积实际是这两条边的边长与其夹角的余弦之间的关系,转化后,再根据正弦定理把边的关系转化为角的关系,即可求出角B;(2)所求的数量积中两向量的夹角是已知的,两向量的模之间可以根据余弦定理建立一个等式,只要根据基本不等式即可求出模的乘积的最小值.
第23讲 │ 要点探究
第23讲 │ 要点探究
[点评] 根据正弦定理和余弦定理,实现三角形之间关系的相互转化,然后根据转化后的方程求解三角形的元素是解三角形的基本方法.当三角形中的已知元素不能完全把三角形固定下来时,可以根据正弦定理和余弦定理建立其三角之间的关系,通过这个关系式达到求解最值、范围之类的问题.
规律总结
第23讲 │ 规律总结
1.解决测量问题的基本方法是把测量目标纳入到一个三角形中,这个三角形的一些元素是可以测量出来的,一些元素是可以借助于其他可以测量的三角形求解出来的,通过测量的、求解的元素使这个三角形可解.
2.解决不可及目标的测量、航海问题的计算,要注意各种角的概念,解题时根据这些概念画出图形,然后分析求解目标所在的三角形,在整体中寻找这个三角形可解的条件,然后制订计划具体求解各个三角形.
第23讲 │ 规律总结
