2012届高考复习方案数学理科(北师版)第2单元第11讲 函数与方程
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第2单元第11讲 函数与方程 |
|
|
| 格式 | rar | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 18:07:35 | ||
图片预览






文档简介
(共19张PPT)
第11讲 │ 函数与方程
第11讲 函数与方程
知识梳理
1.一般地,如果函数y=f(x)的图像与横轴有交点,我们把这个交点的________称为这个函数的______.
2.方程f(x)=0有实数根 函数y=f(x)的图像与x轴有______ 函数y=f(x)有______.
3.(1)如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线;(2)并且满足__________.那么,函数y=f(x)在区间(a,b)内有零点,即至少存在一个c∈(a,b),使________.满足上面条件(1)、(2)后,在(a,b)内存在的c不一定只有一个.
第11讲 │ 知识梳理
横坐标
零点
交点
零点
f(a)·f(b)<0
f(c)=0
4.函数f(x)的图像是一条连续的曲线,且在区间[a,b]上有f(a)·f(b)<0,通过不断地选取区间的中点,把函数f(x)所在的零点区间__________,再经比较,按需要留下其中一个小区间的方法称为________.
第11讲 │ 知识梳理
一分为二
二分法
要点探究
探究点1 方程的根与函数的零点
第11讲 │ 要点探究
[思路] 分别确定分段函数在各段解析式中的零点个数.
[答案] B
第11讲 │ 要点探究
[解析] 当x≤0时,令x2+2x-3=0,解得x=-3;当x>0时,令-2+lnx=0,解得x=e2,所以已知函数有2个零点,选B.
[点评] 函数f(x)的零点是一个实数(不是点),就是方程f(x)=0的实数根,也是函数y=f(x)的图像与x轴的交点的横坐标,因此判断零点的个数就是判断方程f(x)=0的实根个数,有时也可以根据函数图像的交点来判断零点的个数,如:
第11讲 │ 要点探究
函数y=lnx+2x-6的零点个数为________.
[答案] 一个
[解析] 在同一坐标系画出y=lnx与y=6-2x的图像,由图可知两图像只有一个交点,故函数y=lnx+2x-6只有一个零点.
探究点2 函数零点位置的判断
第11讲 │ 要点探究
[思路] 对于区间上连续不断的函数,在区间[a,b]内寻根,往往需要利用零点的存在性定理判断,即判断f(a)f(b)<0是否成立.
例2 判断下列函数在给定区间上是否存在零点.
(1)f(x)=x2-3x-18,x∈[1,8];
(2)f(x)=x3-x-1,x∈[-1,2];
(3)f(x)=log2(x+2)-x,x∈[1,3].
第11讲 │ 要点探究
[解答] (1)方法一:因为f(1)=-20<0,f(8)=22>0,所以f(1)·f(8)<0,故f(x)=x2-3x-18在x∈[1,8]上存在零点.
方法二:令x2-3x-18=0,解得x=-3或6,所以函数f(x)=x2-3x-18在x∈[1,8]上存在零点.
(2)∵f(-1)=-1<0,f(2)=5>0,∴f(x)=x3-x-1在x∈[-1,2]上存在零点.
(3)∵f(1)=log2(1+2)-1=log23-1>0,f(3)=log2(3+2)-3=log25-3<0,∴f(1)·f(3)<0,故f(x)=log2(x+2)-x在x∈[1,3]上存在零点.
[点评] 零点的存在性定理是判断连续不断的函数在区间[a,b]上是否存在零点的定理,该定理只能判断存在零点,不能判断区间[a,b]不存在零点,即如果函数y=f(x)在区间[a,b]上有f(a)f(b)>0,函数在区间[a,b]上也可能存在零点,如:
第11讲 │ 要点探究
[答案] D
[2009·天津卷] 设函数f(x)=x-lnx(x>0),则y=f(x)( )
A.在区间,(1,e)内均有零点
B.在区间,(1,e)内均无零点
C.在区间内有零点,在区间(1,e)内无零点
D.在区间内无零点,在区间(1,e)内有零点
[解答] 由题意得f′(x)=-=,令f′(x)>0,得x>3;令f′(x)<0,得00,故选择D.
探究点3 二次函数零点的分布问题
例3 已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围;
(2)若方程两根均在区间(0,1)内,求m的范围.
第11讲 │ 要点探究
[思路] 设出二次方程对应的函数,可画出相应的示意图,然后用函数性质加以限制.
[点评]本题综合考查了二次函数、二次方程以及二次不等式等的基本关系,有效地训练对“三个二次”的整体理解与掌握,解题过程中的数形结合是数学的重要思想方法.
第11讲 │ 要点探究
第11讲 │ 要点探究
第11讲 │ 要点探究
求a为何值时,方程9-|x-2|-4·3-|x-2|-a=0有实根.
探究点4 利用函数零点求参数
例4 (1)若函数f(x)=ax2-x-1有且仅有一个零点,求实数a的值;
第11讲 │ 要点探究
[思路] 函数的类型为初等函数,因此可以利用方程的思想求解
第11讲 │ 要点探究
[思路]通过图像变换法作出函数的图像,利用数形结合思想求解.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
[解答] 若f(x)=|4x-x2|+a有4个零点,即|4x-x2|+a=0有四个根,即|4x-x2|=-a有四个根.令g(x)=|4x-x2|,h(x)=-a.作出g(x)、h(x)的图像,由图像可知如果要使|4x-x2|=-a有四个根,那么g(x)与h(x)的图像应有4个交点.故需满足0<-a<4,即-4<a<0.∴a的取值范围是(-4,0).
第11讲 │ 要点探究
[点评] 函数形结合法是解决利用函数零点求参数问题的基本思想,其要点是通过构造函数,把函数的零点问题转化为两个函数图像的交点问题.
第11讲 │ 要点探究
已知函数f(x)=x|x-4|-5,当方程f(x)=a有三个根时,求实数a的取值范围.
规律总结
第11讲 │ 规律总结
1.方程的根(从数的角度看)、函数图像与x轴的交点的横坐标(从形的角度看)、函数的零点是同一个问题的三种不同的表现形式.
2.函数零点的求法:
(1)代数法:利用公式法、因式分解法、直接法求方程f(x)=0的根.
(2)几何法:对于不能用求根公式的方程,可以将它与函数y=f(x)的图像联系起来,并利用函数的性质找出零点.
(3)二分法:主要用于求函数零点的近似值.
第11讲 │ 规律总结
3.要注意对于在区间[a,b]上的连续函数f(x),若x0是f(x)的零点,却不一定有f(a)·f(b)<0,即f(a)·f(b)<0仅是f(x)在[a,b]上存在零点的充分条件,而不是必要条件.
4.有关函数零点的重要结论
(1)若连续不断的函数f(x)是定义域上的单调函数,则f(x)至多一个零点.
(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.
(3)连续不断的函数图像通过零点时,函数值符号可能不变,也可能改变.
5.用二分法求零点的近似解时,所要求的精确度ε不同,得到的结果也不同.精确度为ε是指在计算过程中得到某个区间(a,b)后,若其长度小于ε,即认为已达到所要求的精确度,可停止计算.精确度为0.001与精确到0.001是不同的.
第11讲 │ 函数与方程
第11讲 函数与方程
知识梳理
1.一般地,如果函数y=f(x)的图像与横轴有交点,我们把这个交点的________称为这个函数的______.
2.方程f(x)=0有实数根 函数y=f(x)的图像与x轴有______ 函数y=f(x)有______.
3.(1)如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线;(2)并且满足__________.那么,函数y=f(x)在区间(a,b)内有零点,即至少存在一个c∈(a,b),使________.满足上面条件(1)、(2)后,在(a,b)内存在的c不一定只有一个.
第11讲 │ 知识梳理
横坐标
零点
交点
零点
f(a)·f(b)<0
f(c)=0
4.函数f(x)的图像是一条连续的曲线,且在区间[a,b]上有f(a)·f(b)<0,通过不断地选取区间的中点,把函数f(x)所在的零点区间__________,再经比较,按需要留下其中一个小区间的方法称为________.
第11讲 │ 知识梳理
一分为二
二分法
要点探究
探究点1 方程的根与函数的零点
第11讲 │ 要点探究
[思路] 分别确定分段函数在各段解析式中的零点个数.
[答案] B
第11讲 │ 要点探究
[解析] 当x≤0时,令x2+2x-3=0,解得x=-3;当x>0时,令-2+lnx=0,解得x=e2,所以已知函数有2个零点,选B.
[点评] 函数f(x)的零点是一个实数(不是点),就是方程f(x)=0的实数根,也是函数y=f(x)的图像与x轴的交点的横坐标,因此判断零点的个数就是判断方程f(x)=0的实根个数,有时也可以根据函数图像的交点来判断零点的个数,如:
第11讲 │ 要点探究
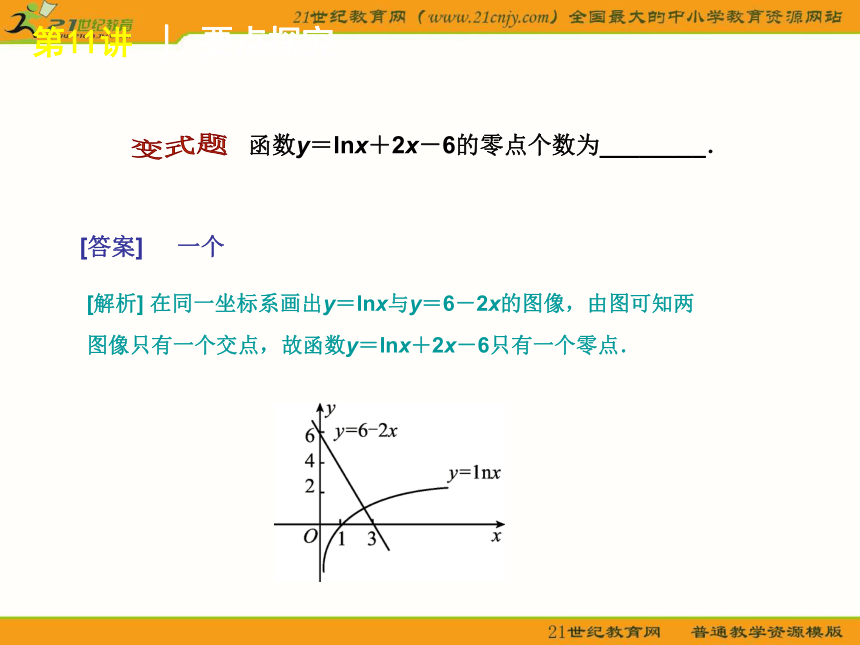
函数y=lnx+2x-6的零点个数为________.
[答案] 一个
[解析] 在同一坐标系画出y=lnx与y=6-2x的图像,由图可知两图像只有一个交点,故函数y=lnx+2x-6只有一个零点.
探究点2 函数零点位置的判断
第11讲 │ 要点探究
[思路] 对于区间上连续不断的函数,在区间[a,b]内寻根,往往需要利用零点的存在性定理判断,即判断f(a)f(b)<0是否成立.
例2 判断下列函数在给定区间上是否存在零点.
(1)f(x)=x2-3x-18,x∈[1,8];
(2)f(x)=x3-x-1,x∈[-1,2];
(3)f(x)=log2(x+2)-x,x∈[1,3].
第11讲 │ 要点探究
[解答] (1)方法一:因为f(1)=-20<0,f(8)=22>0,所以f(1)·f(8)<0,故f(x)=x2-3x-18在x∈[1,8]上存在零点.
方法二:令x2-3x-18=0,解得x=-3或6,所以函数f(x)=x2-3x-18在x∈[1,8]上存在零点.
(2)∵f(-1)=-1<0,f(2)=5>0,∴f(x)=x3-x-1在x∈[-1,2]上存在零点.
(3)∵f(1)=log2(1+2)-1=log23-1>0,f(3)=log2(3+2)-3=log25-3<0,∴f(1)·f(3)<0,故f(x)=log2(x+2)-x在x∈[1,3]上存在零点.
[点评] 零点的存在性定理是判断连续不断的函数在区间[a,b]上是否存在零点的定理,该定理只能判断存在零点,不能判断区间[a,b]不存在零点,即如果函数y=f(x)在区间[a,b]上有f(a)f(b)>0,函数在区间[a,b]上也可能存在零点,如:
第11讲 │ 要点探究
[答案] D
[2009·天津卷] 设函数f(x)=x-lnx(x>0),则y=f(x)( )
A.在区间,(1,e)内均有零点
B.在区间,(1,e)内均无零点
C.在区间内有零点,在区间(1,e)内无零点
D.在区间内无零点,在区间(1,e)内有零点
[解答] 由题意得f′(x)=-=,令f′(x)>0,得x>3;令f′(x)<0,得0
探究点3 二次函数零点的分布问题
例3 已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围;
(2)若方程两根均在区间(0,1)内,求m的范围.
第11讲 │ 要点探究
[思路] 设出二次方程对应的函数,可画出相应的示意图,然后用函数性质加以限制.
[点评]本题综合考查了二次函数、二次方程以及二次不等式等的基本关系,有效地训练对“三个二次”的整体理解与掌握,解题过程中的数形结合是数学的重要思想方法.
第11讲 │ 要点探究
第11讲 │ 要点探究
第11讲 │ 要点探究
求a为何值时,方程9-|x-2|-4·3-|x-2|-a=0有实根.
探究点4 利用函数零点求参数
例4 (1)若函数f(x)=ax2-x-1有且仅有一个零点,求实数a的值;
第11讲 │ 要点探究
[思路] 函数的类型为初等函数,因此可以利用方程的思想求解
第11讲 │ 要点探究
[思路]通过图像变换法作出函数的图像,利用数形结合思想求解.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
[解答] 若f(x)=|4x-x2|+a有4个零点,即|4x-x2|+a=0有四个根,即|4x-x2|=-a有四个根.令g(x)=|4x-x2|,h(x)=-a.作出g(x)、h(x)的图像,由图像可知如果要使|4x-x2|=-a有四个根,那么g(x)与h(x)的图像应有4个交点.故需满足0<-a<4,即-4<a<0.∴a的取值范围是(-4,0).
第11讲 │ 要点探究
[点评] 函数形结合法是解决利用函数零点求参数问题的基本思想,其要点是通过构造函数,把函数的零点问题转化为两个函数图像的交点问题.
第11讲 │ 要点探究
已知函数f(x)=x|x-4|-5,当方程f(x)=a有三个根时,求实数a的取值范围.
规律总结
第11讲 │ 规律总结
1.方程的根(从数的角度看)、函数图像与x轴的交点的横坐标(从形的角度看)、函数的零点是同一个问题的三种不同的表现形式.
2.函数零点的求法:
(1)代数法:利用公式法、因式分解法、直接法求方程f(x)=0的根.
(2)几何法:对于不能用求根公式的方程,可以将它与函数y=f(x)的图像联系起来,并利用函数的性质找出零点.
(3)二分法:主要用于求函数零点的近似值.
第11讲 │ 规律总结
3.要注意对于在区间[a,b]上的连续函数f(x),若x0是f(x)的零点,却不一定有f(a)·f(b)<0,即f(a)·f(b)<0仅是f(x)在[a,b]上存在零点的充分条件,而不是必要条件.
4.有关函数零点的重要结论
(1)若连续不断的函数f(x)是定义域上的单调函数,则f(x)至多一个零点.
(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.
(3)连续不断的函数图像通过零点时,函数值符号可能不变,也可能改变.
5.用二分法求零点的近似解时,所要求的精确度ε不同,得到的结果也不同.精确度为ε是指在计算过程中得到某个区间(a,b)后,若其长度小于ε,即认为已达到所要求的精确度,可停止计算.精确度为0.001与精确到0.001是不同的.
