2012届高考复习方案数学理科(北师版)第2单元第12讲 函数模型及其应用
文档属性
| 名称 | 2012届高考复习方案数学理科(北师版)第2单元第12讲 函数模型及其应用 |
|
|
| 格式 | rar | ||
| 文件大小 | 120.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-16 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第12讲 │ 函数模型及其应用
第12讲 函数模型及其应用
知识梳理
1.函数模型
常用函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0).
(2)二次函数模型:f(x)=ax2+bx+c(a、b、c为常数,a≠0).
(3)指数函数模型:f(x)=abx+c(a、b、c为常数,a≠0,b>0,b≠1).
(4)对数函数模型:f(x)=mlogax+n(m、n、a为常数,a>0,m≠0,a≠1).
(5)幂函数模型:f(x)=axn+b(a、b、n为常数,a≠0,n≠1).
(6)分段函数模型
第12讲 │ 知识梳理
2.三种函数模型的性质
在区间(0,+∞)上,指数函数y=ax(a>1),对数函数y=logax(a>1),幂函数y=xn(n>0)都是增函数,但它们增长速度不同.随着x的增大,指数函数y=ax(a>1)的增长速度越来越快,会超过并远远大于幂函数y=xn(n>0)的增长速度,而对数函数y=logax(a>1)的增长速度则会越来越慢,图像逐渐表示为与x轴趋于平行,因此,总会存在一个x0,当x>x0时,就有logax第12讲 │ 知识梳理
第12讲 │ 知识梳理
3.函数模型的应用
(1)解答函数应用题的步骤:
①阅读理解:读懂题目中的文字叙述所反映的实际背景,领悟其中的数学本质,弄清题中出现的量及其数学含义.
②分析建模:分析题目中的量与量之间的关系,根据题意恰当地引入字母(包括常量与变量),有时可借助列表、画图等手段来理顺数量关系,同时要注意由已知条件联想熟知的函数模型,以确定函数模型的种类,在对已知条件和目标变量的综合分析、归纳抽象的基础上,建立目标函数,将实际问题转化为数学问题.
③数学求解:利用相关的函数知识,进行合理设计,以确定最佳解题方案,进行数学上的求解计算.
④还原总结:把计算获得的结果还原到实际问题中去解释实际问题,即对实际问题进行总结作答.
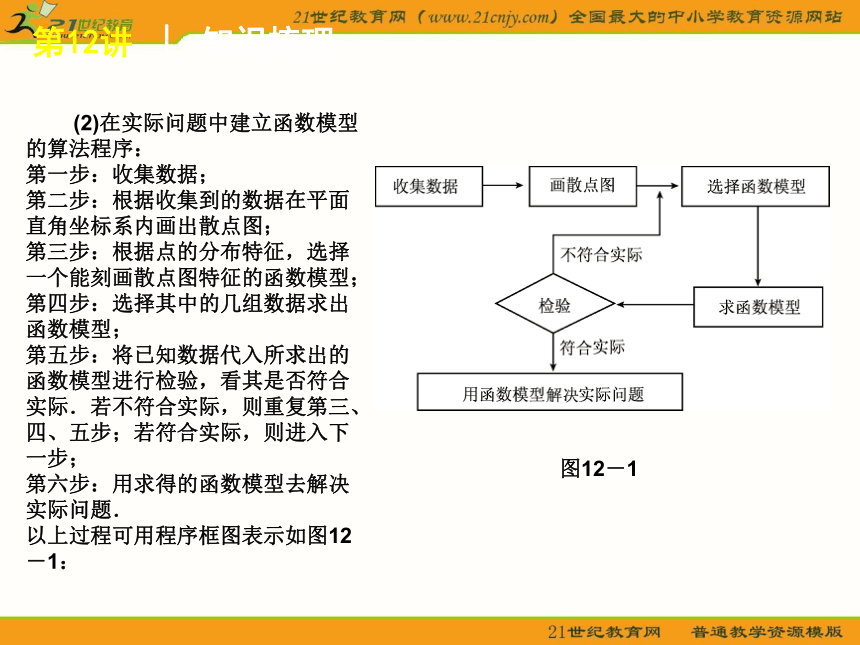
(2)在实际问题中建立函数模型的算法程序:
第一步:收集数据;
第二步:根据收集到的数据在平面直角坐标系内画出散点图;
第三步:根据点的分布特征,选择一个能刻画散点图特征的函数模型;
第四步:选择其中的几组数据求出函数模型;
第五步:将已知数据代入所求出的函数模型进行检验,看其是否符合实际.若不符合实际,则重复第三、四、五步;若符合实际,则进入下一步;
第六步:用求得的函数模型去解决实际问题.
以上过程可用程序框图表示如图12-1:
第12讲 │ 知识梳理
图12-1
要点探究
探究点1 已知函数模型解决实际应用问题
例1 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y与销售单价x(元/件)的图像可近似看作一条直线,该直线经过(600,400)和(700,300)两点.
(1)求y关于x的函数关系式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,试用销售单价x表示毛利润S,并求销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时销售量是多少?
第12讲 │ 要点探究
第12讲 │ 要点探究
[思路]根据函数图像,可知y是x的一次函数,利用待定系数法可求得函数关系式;然后利用“毛利润=销售总价-成本总价”建立S与x的关系式,通过求函数的最值达到解题目的.
第12讲 │ 要点探究
[点评] 以函数图像给出关系式的应用问题,先利用图像形状确定函数的类型,然后利用待定系数法求解;函数应用问题中,已知的等量关系也是解题的依据,它们常用来构造函数关系.
第12讲 │ 要点探究
第12讲 │ 要点探究
[思路] 要弄清楚题目提供的数据、所求数据与函数中的自变量、函数值之间的对应关系.
第12讲 │ 要点探究
[点评] 已知函数模型解决问题,实质上就是利用函数模型求值或考查函数的性质,这类问题通常要把问题与函数的性质对应起来,比较注意运算能力的考查.
探究点2 建立函数模型解决实际应用问题
第12讲 │ 要点探究
例3 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图像如图12-2所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)时间内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
第12讲 │ 要点探究
图12-2
第12讲 │ 要点探究
[思路] 根据函数图像,利用待定系数求得分段函数各段的关系式,再结合函数的性质求解.
第12讲 │ 要点探究
第12讲 │ 要点探究
[点评] 分段函数是一类重要的函数,生活中很多实例都是分段函数的模型,解决此类问题主要是构造分段函数,然后根据自变量不同的取值范围选择相应的解析式求解,因此,解决分段函数中问题常与分类讨论思想相结合.另外,构造分段函数时要力求准确、简捷,做到分段合理,不重不漏.
第12讲 │ 要点探究
例4 芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10 kg)与上市时间t(单位:天)的数据情况如下表:
第12讲 │ 要点探究
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt;
(2)利用你选择的函数,求芦荟种植成本最低时上市天数及最低种植成本.
[思路] 要选择最能反映芦荟种植成本与上市时间之间的变化关系的函数式,应该分析各函数的发展情况,通过研究这些函数的变化趋势与表格提供的数据是否相符来判断哪个函数最优.
第12讲 │ 要点探究
第12讲 │ 要点探究
[点评] 对数据进行函数模拟,选择最符合的模拟函数,可先散点图,然后作出模拟函数的图像,选择适合的几种函数,然后结合这几种函数的性质和数据特点加以验证.
规律总结
第12讲 │ 规律总结
1.把实际问题数学化、建立数学模型一定要过好三关:
(1)事理关:通过阅读、理解,明白问题讲的是什么,熟悉实际背景,为解题找突破口.
(2)文理关:将实际问题的文字语言转化为数学符号语言,用数学式子表达数学关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
第12讲 │ 规律总结
2.高考数学试题中联系生活实际和生产实际的应用问题,其创意新颖,设问角度独特,解题方法灵活,一般文字叙述长,数量关系分散且难以把握,解决此类问题的关键要认真审题,确切理解题意,进行科学的抽象概括,将实际问题归纳为相应的数学问题,然后利用函数、方程、不等式等有关知识解答.
3.解答数学应用题时,一定要注意函数的定义域,否则极易出错.
第12讲 │ 函数模型及其应用
第12讲 函数模型及其应用
知识梳理
1.函数模型
常用函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0).
(2)二次函数模型:f(x)=ax2+bx+c(a、b、c为常数,a≠0).
(3)指数函数模型:f(x)=abx+c(a、b、c为常数,a≠0,b>0,b≠1).
(4)对数函数模型:f(x)=mlogax+n(m、n、a为常数,a>0,m≠0,a≠1).
(5)幂函数模型:f(x)=axn+b(a、b、n为常数,a≠0,n≠1).
(6)分段函数模型
第12讲 │ 知识梳理
2.三种函数模型的性质
在区间(0,+∞)上,指数函数y=ax(a>1),对数函数y=logax(a>1),幂函数y=xn(n>0)都是增函数,但它们增长速度不同.随着x的增大,指数函数y=ax(a>1)的增长速度越来越快,会超过并远远大于幂函数y=xn(n>0)的增长速度,而对数函数y=logax(a>1)的增长速度则会越来越慢,图像逐渐表示为与x轴趋于平行,因此,总会存在一个x0,当x>x0时,就有logax
第12讲 │ 知识梳理
3.函数模型的应用
(1)解答函数应用题的步骤:
①阅读理解:读懂题目中的文字叙述所反映的实际背景,领悟其中的数学本质,弄清题中出现的量及其数学含义.
②分析建模:分析题目中的量与量之间的关系,根据题意恰当地引入字母(包括常量与变量),有时可借助列表、画图等手段来理顺数量关系,同时要注意由已知条件联想熟知的函数模型,以确定函数模型的种类,在对已知条件和目标变量的综合分析、归纳抽象的基础上,建立目标函数,将实际问题转化为数学问题.
③数学求解:利用相关的函数知识,进行合理设计,以确定最佳解题方案,进行数学上的求解计算.
④还原总结:把计算获得的结果还原到实际问题中去解释实际问题,即对实际问题进行总结作答.
(2)在实际问题中建立函数模型的算法程序:
第一步:收集数据;
第二步:根据收集到的数据在平面直角坐标系内画出散点图;
第三步:根据点的分布特征,选择一个能刻画散点图特征的函数模型;
第四步:选择其中的几组数据求出函数模型;
第五步:将已知数据代入所求出的函数模型进行检验,看其是否符合实际.若不符合实际,则重复第三、四、五步;若符合实际,则进入下一步;
第六步:用求得的函数模型去解决实际问题.
以上过程可用程序框图表示如图12-1:
第12讲 │ 知识梳理
图12-1
要点探究
探究点1 已知函数模型解决实际应用问题
例1 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y与销售单价x(元/件)的图像可近似看作一条直线,该直线经过(600,400)和(700,300)两点.
(1)求y关于x的函数关系式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,试用销售单价x表示毛利润S,并求销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时销售量是多少?
第12讲 │ 要点探究
第12讲 │ 要点探究
[思路]根据函数图像,可知y是x的一次函数,利用待定系数法可求得函数关系式;然后利用“毛利润=销售总价-成本总价”建立S与x的关系式,通过求函数的最值达到解题目的.
第12讲 │ 要点探究
[点评] 以函数图像给出关系式的应用问题,先利用图像形状确定函数的类型,然后利用待定系数法求解;函数应用问题中,已知的等量关系也是解题的依据,它们常用来构造函数关系.
第12讲 │ 要点探究
第12讲 │ 要点探究
[思路] 要弄清楚题目提供的数据、所求数据与函数中的自变量、函数值之间的对应关系.
第12讲 │ 要点探究
[点评] 已知函数模型解决问题,实质上就是利用函数模型求值或考查函数的性质,这类问题通常要把问题与函数的性质对应起来,比较注意运算能力的考查.
探究点2 建立函数模型解决实际应用问题
第12讲 │ 要点探究
例3 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图像如图12-2所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)时间内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
第12讲 │ 要点探究
图12-2
第12讲 │ 要点探究
[思路] 根据函数图像,利用待定系数求得分段函数各段的关系式,再结合函数的性质求解.
第12讲 │ 要点探究
第12讲 │ 要点探究
[点评] 分段函数是一类重要的函数,生活中很多实例都是分段函数的模型,解决此类问题主要是构造分段函数,然后根据自变量不同的取值范围选择相应的解析式求解,因此,解决分段函数中问题常与分类讨论思想相结合.另外,构造分段函数时要力求准确、简捷,做到分段合理,不重不漏.
第12讲 │ 要点探究
例4 芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10 kg)与上市时间t(单位:天)的数据情况如下表:
第12讲 │ 要点探究
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt;
(2)利用你选择的函数,求芦荟种植成本最低时上市天数及最低种植成本.
[思路] 要选择最能反映芦荟种植成本与上市时间之间的变化关系的函数式,应该分析各函数的发展情况,通过研究这些函数的变化趋势与表格提供的数据是否相符来判断哪个函数最优.
第12讲 │ 要点探究
第12讲 │ 要点探究
[点评] 对数据进行函数模拟,选择最符合的模拟函数,可先散点图,然后作出模拟函数的图像,选择适合的几种函数,然后结合这几种函数的性质和数据特点加以验证.
规律总结
第12讲 │ 规律总结
1.把实际问题数学化、建立数学模型一定要过好三关:
(1)事理关:通过阅读、理解,明白问题讲的是什么,熟悉实际背景,为解题找突破口.
(2)文理关:将实际问题的文字语言转化为数学符号语言,用数学式子表达数学关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
第12讲 │ 规律总结
2.高考数学试题中联系生活实际和生产实际的应用问题,其创意新颖,设问角度独特,解题方法灵活,一般文字叙述长,数量关系分散且难以把握,解决此类问题的关键要认真审题,确切理解题意,进行科学的抽象概括,将实际问题归纳为相应的数学问题,然后利用函数、方程、不等式等有关知识解答.
3.解答数学应用题时,一定要注意函数的定义域,否则极易出错.
