浙教版高中信息技术 必修一 1.2 计算机编码(进制转换)(24张幻灯片)
文档属性
| 名称 | 浙教版高中信息技术 必修一 1.2 计算机编码(进制转换)(24张幻灯片) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2020-07-22 13:03:41 | ||
图片预览





文档简介
计算机的编码
刘盈盈
二进制 、十六进制、字符、汉字 编码
计算机内的编码
冯.诺依曼(计算机之父)
提出计算机信息编码采用二进制形式,
即在计算机内部用0和1表示所有信息;
采用二进制编码的原因:二进制中只有“0”和“1”两个符号,能方便地表示电子计算机中电子器件的状态的变化。
计算机内的编码
汉字
图像
声音
视频
A
字符
123
十进制数字
计算机是如何
对这些信息进行编码的呢?
十进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
个数
★
1
★★
2
★★★
3
★★★★
4
★★★★★
5
★★★★★★
6
★★★★★★★
7
★★★★★★★★
8
★★★★★★★★★
9
★★★★★★★★★★
10
★★★★★★★★★★★
11
★★★★★★★★★★★★
12
★★★★★★★★★★★★★
13
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
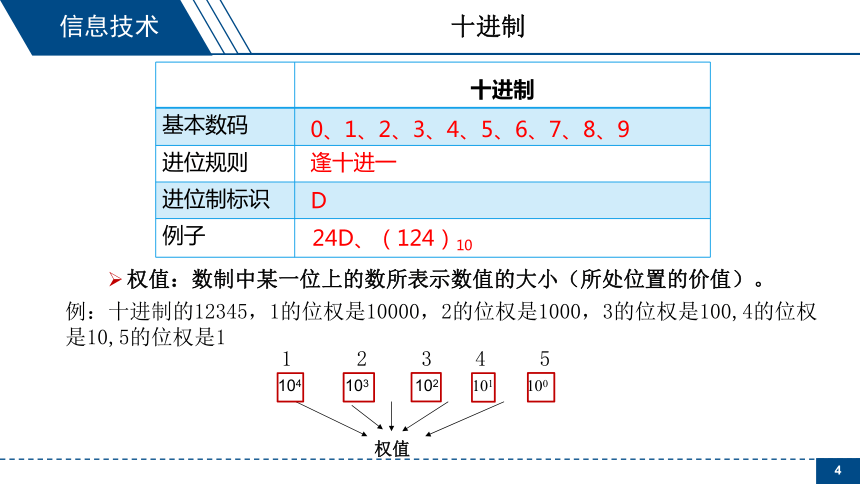
十进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
12345=1×10000 +2×1000+3×100+4×10+5×1
=1×104 +2×103 +3×102+4×101+5×100
权值
权值:数制中某一位上的数所表示数值的大小(所处位置的价值)。
例:十进制的12345,1的位权是10000,2的位权是1000,3的位权是100,4的位权是10,5的位权是1
1 2 3 4 5
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
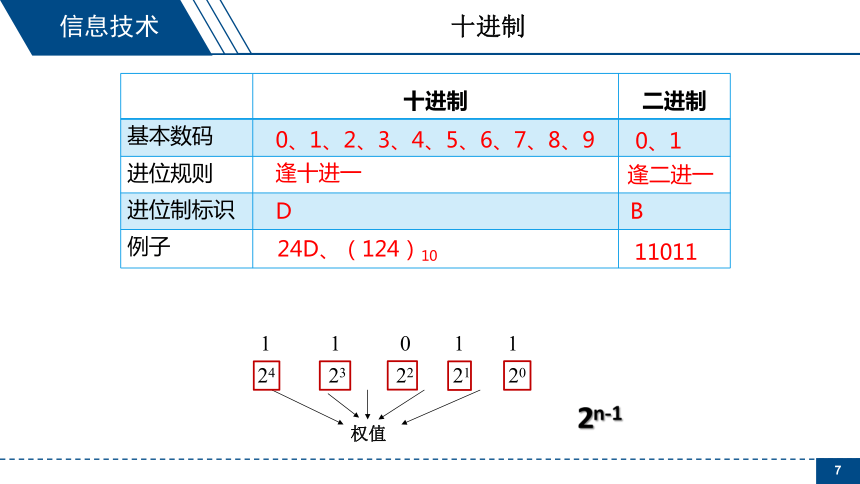
十进制
二进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
二进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
十进制
二进制
★
1
★★
2
★★★
3
★★★★
4
★★★★★
5
★★★★★★
6
★★★★★★★
7
★★★★★★★★
8
★★★★★★★★★
9
★★★★★★★★★★
10
★★★★★★★★★★★
11
★★★★★★★★★★★★
12
★★★★★★★★★★★★★
13
1×24 +1×23 +0×22 +121 × 20
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
1 1 0 1 1
权值
11011
2n-1
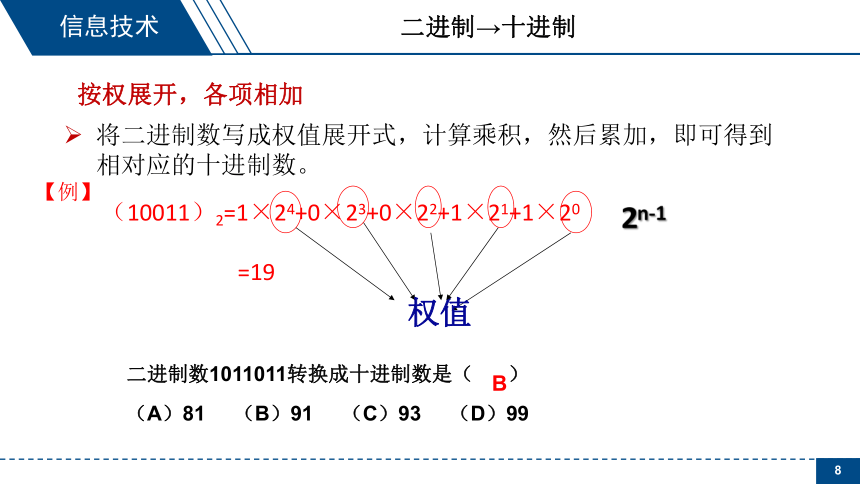
二进制→十进制
将二进制数写成权值展开式,计算乘积,然后累加,即可得到相对应的十进制数。
按权展开,各项相加
2n-1
权值
(10011)2=1×24+0×23+0×22+1×21+1×20
【例】
二进制数1011011转换成十进制数是( )
(A)81???? (B)91???? (C)93???? (D)99
B
=19
二进制→十进制
记住“8421”
例如:(110101)2=(53)10
二进制数:
权值:
技巧:
=53
1 1 0 1 0 1
换算:
1×32 +1×16 +0×8 +1×4+0×2+1×1
32 16 8 4 2 1
十进制→二进制
除2取余,逆序输出
(28)10=(11100)2
十进制数除以2,取出余数1或0作为相应二进制数的最低位,把得到的商再除以2,再取余,依次类推,直到商为0。
十进制数71转换成二进制数是( )
(A)(1000111)2 (B)(1110001)2
(C)(1001100)2 (D)(1000011)2
A
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
十六进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
0~9,A~F
逢十六进一
H
11B、
(10)2
十六进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
十
二
十六
星星
十
二
十六
0
0
★★★★★★★★
8
1000
★
1
1
★★★★★★★★★
9
1001
★★
2
10
★★★★★★★★★★
10
1010
★★★
3
11
★★★★★★★★★★★
11
1011
★★★★
4
100
★★★★★★★★★★★★
12
1100
★★★★★
5
101
★★★★★★★★★★★★★
13
1101
★★★★★★
6
110
★★★★★★★★★★★★★★
14
1110
★★★★★★★
7
111
★★★★★★★★★★★★★★★
15
1111
十六进制
×164 +1×163 ×162 +1161 ×160
4 D 0 9 A
权值
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
十六进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
0~9,A~F
逢十六进一
H
11B、
(10)2
1AH、
(C0)16
16n-1
“按权位展开相加”
例如:(A12)16=( )10
(A12)16=A×162+1×161+2×160=10×256+1×161+2×160=2578D
练:十六进制转化为十进制
1ABH=____________________D
101H=____________________D
十六进制数
A
1
2
权 值
162
161
160
427
257
十六进制→十进制
“除16取余、逆序输出”
例如:(1000)10=( )16
余数逆序输出后结果为:3 14 8 用十六进制表示为3E8,(1000)10=(3E8)16
练:十进制转换为十六进制
147D=__________H 1024D=___________H
十进制→十六进制
93
400
二进制?十六进制
二进制
十六进制
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
十进制
四缩一,一放四
把二进制数由低位到高位,每四位分割(不满四位用0填充),分割后的每四位二进制转化为相应的10进制,最后用16进制表示。
111 1010
7
A
7
10
2进制
10进制
16进制
【牛刀小试】二进制数(11011001)2转换成十六进制数是( )
(A)D9H (B)9DH (C)6DH (D)D6H
A
0
算式1011B + 10D的运算结果是( )
A.11101B B.51H
C.15H D.20D
答案:C
解析:1011B转换成十进制=1×23+0×22+1×21++1×20=8+0+2+1=11D,算式1011B + 10D的运算结果21D。 A答案11101B转换成十进制=1×24+1×23+1×22+0×21+1×20=16+8+4+0+1=29D,B答案51H转换成十进制=5 ×161+1×160=81D, C答案15H转换成十进制=1 ×161+5×160=21D, B答案20D明显不符,所以正确答案为C。
十进制
二进制
十六进制
除二取余
除十六取余
权值相加
权值相加
四合一
一拆四
思考:M进制怎么与十进制互换?
思考:
(1)1位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是____________。
(2)2位二进制能表示______________个不同数字,能表示的最大数转换成十进制是____________。
(3)3位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是_____________。
(4)n位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是_____________。
2
1
4
3
8
7
2n
2n-1
存储量级
1.最小单位:
二进制位(比特、bit或b)
基本单位及换算:
8个位(比特)=1个字节 8bit=1Byte 8b=1B
存储容量单位有:B、KB,MB,GB,TB。
1KB=1024B(千字节)
1MB=1024KB(兆字节)
1GB=1024MB(千兆字节)
1TB=1024GB(百万兆字节)
有一系列相同大小的照片、每张照片24MB,一存储容量为16GB的U盘可存储该系列照片多少张( )
A.682张 B.683张
C.699084张 D.699085张
答案:A
解析:1GB=1024MB,容量为16GB的U盘,将其转化为MB,16GB=16×1024MB=16384MB,每张照片24MB,所以能存储的照片数=U盘容量(MB)÷24=16384÷24≈682.7张,计算存储数量的时候只能用去尾法计数,所以本题能存储的照片张数为682张。
字符如何用二进制表示?
字符编码
字符及字符编码
字符:是指英文字母和各种符号,包括数字符号、运算符号、标点和分隔符号、各种特殊符号等等
所谓字符编码:就是规定如何用二进制数来表示字符
目前国际上最广泛使用的字符编码是:“美国信息交换标准码”(American Standard Code for Internation Interchange)简称ASCII码。
ASCII码
刘盈盈
二进制 、十六进制、字符、汉字 编码
计算机内的编码
冯.诺依曼(计算机之父)
提出计算机信息编码采用二进制形式,
即在计算机内部用0和1表示所有信息;
采用二进制编码的原因:二进制中只有“0”和“1”两个符号,能方便地表示电子计算机中电子器件的状态的变化。
计算机内的编码
汉字
图像
声音
视频
A
字符
123
十进制数字
计算机是如何
对这些信息进行编码的呢?
十进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
个数
★
1
★★
2
★★★
3
★★★★
4
★★★★★
5
★★★★★★
6
★★★★★★★
7
★★★★★★★★
8
★★★★★★★★★
9
★★★★★★★★★★
10
★★★★★★★★★★★
11
★★★★★★★★★★★★
12
★★★★★★★★★★★★★
13
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
12345=1×10000 +2×1000+3×100+4×10+5×1
=1×104 +2×103 +3×102+4×101+5×100
权值
权值:数制中某一位上的数所表示数值的大小(所处位置的价值)。
例:十进制的12345,1的位权是10000,2的位权是1000,3的位权是100,4的位权是10,5的位权是1
1 2 3 4 5
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
二进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
十进制
二进制
★
1
★★
2
★★★
3
★★★★
4
★★★★★
5
★★★★★★
6
★★★★★★★
7
★★★★★★★★
8
★★★★★★★★★
9
★★★★★★★★★★
10
★★★★★★★★★★★
11
★★★★★★★★★★★★
12
★★★★★★★★★★★★★
13
1×24 +1×23 +0×22 +121 × 20
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
1 1 0 1 1
权值
11011
2n-1
二进制→十进制
将二进制数写成权值展开式,计算乘积,然后累加,即可得到相对应的十进制数。
按权展开,各项相加
2n-1
权值
(10011)2=1×24+0×23+0×22+1×21+1×20
【例】
二进制数1011011转换成十进制数是( )
(A)81???? (B)91???? (C)93???? (D)99
B
=19
二进制→十进制
记住“8421”
例如:(110101)2=(53)10
二进制数:
权值:
技巧:
=53
1 1 0 1 0 1
换算:
1×32 +1×16 +0×8 +1×4+0×2+1×1
32 16 8 4 2 1
十进制→二进制
除2取余,逆序输出
(28)10=(11100)2
十进制数除以2,取出余数1或0作为相应二进制数的最低位,把得到的商再除以2,再取余,依次类推,直到商为0。
十进制数71转换成二进制数是( )
(A)(1000111)2 (B)(1110001)2
(C)(1001100)2 (D)(1000011)2
A
十进制
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
十六进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
0~9,A~F
逢十六进一
H
11B、
(10)2
十六进制
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}星星
十
二
十六
星星
十
二
十六
0
0
★★★★★★★★
8
1000
★
1
1
★★★★★★★★★
9
1001
★★
2
10
★★★★★★★★★★
10
1010
★★★
3
11
★★★★★★★★★★★
11
1011
★★★★
4
100
★★★★★★★★★★★★
12
1100
★★★★★
5
101
★★★★★★★★★★★★★
13
1101
★★★★★★
6
110
★★★★★★★★★★★★★★
14
1110
★★★★★★★
7
111
★★★★★★★★★★★★★★★
15
1111
十六进制
×164 +1×163 ×162 +1161 ×160
4 D 0 9 A
权值
{5DA37D80-6434-44D0-A028-1B22A696006F}
十进制
二进制
十六进制
基本数码
进位规则
进位制标识
例子
0、1、2、3、4、5、6、7、8、9
逢十进一
D
24D、(124)10
0、1
逢二进一
B
0~9,A~F
逢十六进一
H
11B、
(10)2
1AH、
(C0)16
16n-1
“按权位展开相加”
例如:(A12)16=( )10
(A12)16=A×162+1×161+2×160=10×256+1×161+2×160=2578D
练:十六进制转化为十进制
1ABH=____________________D
101H=____________________D
十六进制数
A
1
2
权 值
162
161
160
427
257
十六进制→十进制
“除16取余、逆序输出”
例如:(1000)10=( )16
余数逆序输出后结果为:3 14 8 用十六进制表示为3E8,(1000)10=(3E8)16
练:十进制转换为十六进制
147D=__________H 1024D=___________H
十进制→十六进制
93
400
二进制?十六进制
二进制
十六进制
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
十进制
四缩一,一放四
把二进制数由低位到高位,每四位分割(不满四位用0填充),分割后的每四位二进制转化为相应的10进制,最后用16进制表示。
111 1010
7
A
7
10
2进制
10进制
16进制
【牛刀小试】二进制数(11011001)2转换成十六进制数是( )
(A)D9H (B)9DH (C)6DH (D)D6H
A
0
算式1011B + 10D的运算结果是( )
A.11101B B.51H
C.15H D.20D
答案:C
解析:1011B转换成十进制=1×23+0×22+1×21++1×20=8+0+2+1=11D,算式1011B + 10D的运算结果21D。 A答案11101B转换成十进制=1×24+1×23+1×22+0×21+1×20=16+8+4+0+1=29D,B答案51H转换成十进制=5 ×161+1×160=81D, C答案15H转换成十进制=1 ×161+5×160=21D, B答案20D明显不符,所以正确答案为C。
十进制
二进制
十六进制
除二取余
除十六取余
权值相加
权值相加
四合一
一拆四
思考:M进制怎么与十进制互换?
思考:
(1)1位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是____________。
(2)2位二进制能表示______________个不同数字,能表示的最大数转换成十进制是____________。
(3)3位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是_____________。
(4)n位二进制能表示_____________个不同数字,能表示的最大数转换成十进制是_____________。
2
1
4
3
8
7
2n
2n-1
存储量级
1.最小单位:
二进制位(比特、bit或b)
基本单位及换算:
8个位(比特)=1个字节 8bit=1Byte 8b=1B
存储容量单位有:B、KB,MB,GB,TB。
1KB=1024B(千字节)
1MB=1024KB(兆字节)
1GB=1024MB(千兆字节)
1TB=1024GB(百万兆字节)
有一系列相同大小的照片、每张照片24MB,一存储容量为16GB的U盘可存储该系列照片多少张( )
A.682张 B.683张
C.699084张 D.699085张
答案:A
解析:1GB=1024MB,容量为16GB的U盘,将其转化为MB,16GB=16×1024MB=16384MB,每张照片24MB,所以能存储的照片数=U盘容量(MB)÷24=16384÷24≈682.7张,计算存储数量的时候只能用去尾法计数,所以本题能存储的照片张数为682张。
字符如何用二进制表示?
字符编码
字符及字符编码
字符:是指英文字母和各种符号,包括数字符号、运算符号、标点和分隔符号、各种特殊符号等等
所谓字符编码:就是规定如何用二进制数来表示字符
目前国际上最广泛使用的字符编码是:“美国信息交换标准码”(American Standard Code for Internation Interchange)简称ASCII码。
ASCII码
同课章节目录
- 第一章 信息与信息技术
- 1.1 信息及其特征
- 1.2 信息的编码
- 1.3 信息技术
- 第二章 信息的来源与获取
- 2.1 信息获取的方法
- 2.2 因特网上信息的浏览与获取
- 2.3 网上资源检索
- 2.4 因特网信息资源评价
- 第三章 信息的加工
- 3.1 现代信息处理工具——计算机
- 3.2 字处理和表处理
- 3.3 多媒体信息处理
- 3.4 算法及其实现
- 3.5 智能处理
- 第四章 信息的管理
- 4.1 信息资源管理及其沿革
- 4.2 数据库系统
- 第五章 信息的表达与交流
- 5.1 信息表达
- 5.2 电子邮件
- 5.3 电子公告板、在线游戏
- 第六章 网页的设计与制作
- 6.1 网站和网页
- 6.2 网页制作
- 第七章 信息技术与社会
- 7.1 信息技术对人类社会的影响
- 7.2 知识产权
- 7.3 信息的安全和保护
- 7.4 做信息时代的合格公民
- 非试题类资料
