人教版数学九年级上册24.2.2 直线和圆的位置关系(第一课时)课件(共22张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.2.2 直线和圆的位置关系(第一课时)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 933.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 08:06:56 | ||
图片预览





文档简介
(共22张PPT)
24.2
点和圆、直线和圆的位置关系
第二十四章
圆
24.2.2
直线和圆的位置关系
第1课时
直线和圆的位置关系
人教版数学九年级上册
教学目标
1.通过操作、观察,理解直线和圆有三种位置关系。
2.根据圆心到直线的距离与半径之间的数量关系判定直线和圆的位置关系。
3.经历探索直线和圆的位置关系的判定和专题训练,体验从运动观点以及量变到质变的过程理解直线和圆三种位置关系。
教学重点
直线和圆的位置关系的判定。
教学难点
直线和圆的位置关系的判定。
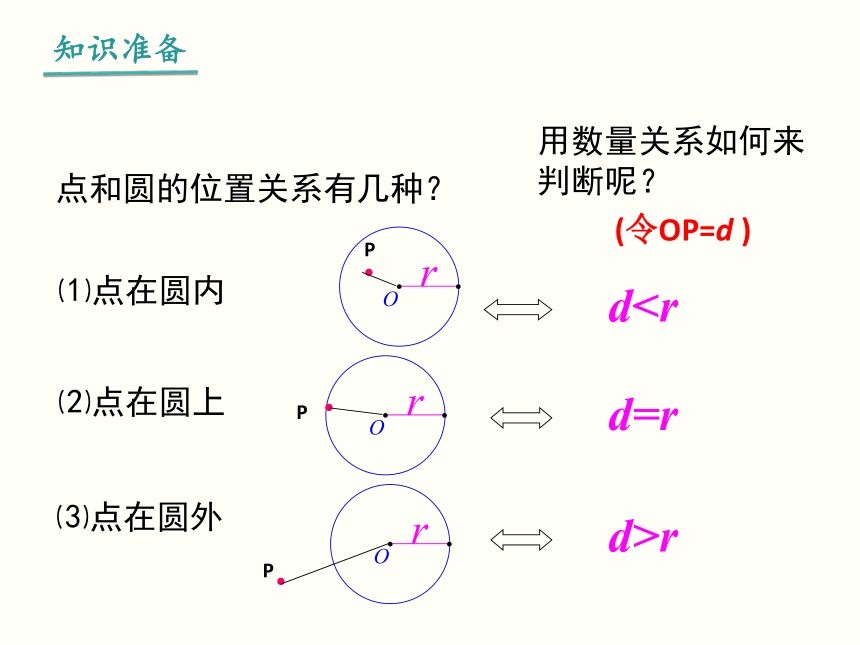
点和圆的位置关系有几种?
dd=r
d>r
用数量关系如何来
判断呢?
(令OP=d
)
知识准备
问题1
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
用定义判断直线与圆的位置关系
探究新知
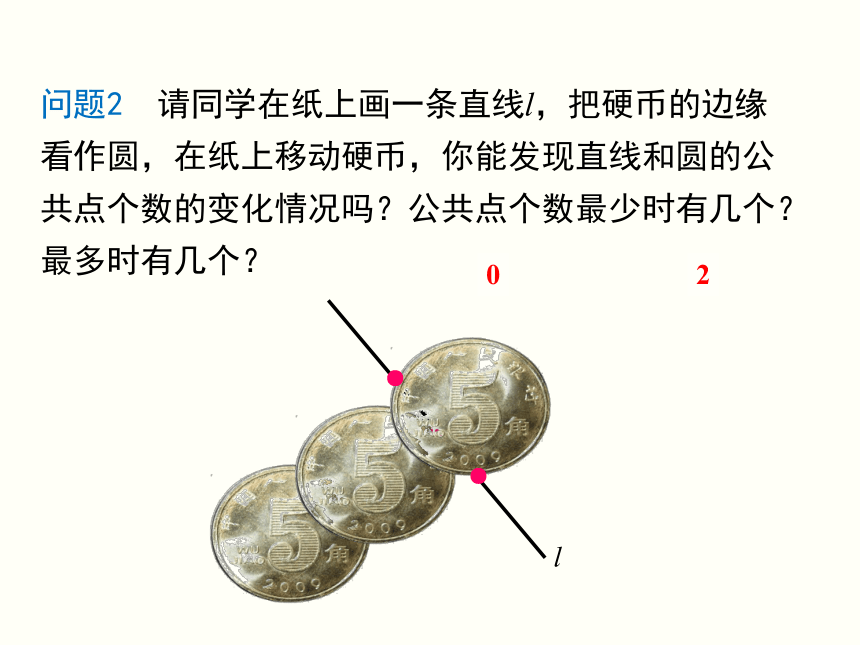
问题2
请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
0
2
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
反复练习
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
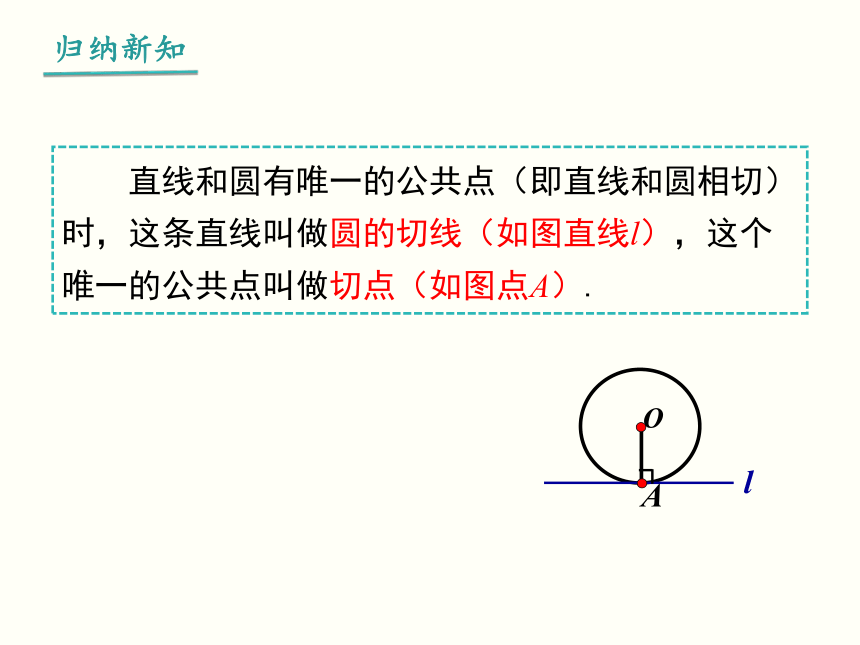
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
归纳新知
1.直线与圆最多有两个公共点.
2.若直线与圆相交,则直线上的点都在圆上.
3.若A是⊙O上一点,则直线AB与⊙O相切.
4.若C为⊙O外一点,则过点C的直线与⊙O相交或相离.
5.直线a
和⊙O有公共点,则直线a与⊙O相交.
√
×
×
×
×
巩固练习
问题1
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
用数量关系判断直线与圆的位置关系
探究新知
问题2
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
归纳新知
相交
相切
相离
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
2
1
0
巩固练习
例1
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)
r=2cm;(2)
r=2.4cm;
(3)
r=3cm.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
典例精析
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以
(1)当r=2cm时,
有d
>r,
因此⊙C和AB相离.
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,有d=r.
因此⊙C和AB相切.
d
(3)当r=3cm时,有d因此,⊙C和AB相交.
d
A
B
C
A
D
4
5
3
变式题:
1.Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心画圆,当半径r为何值时,圆C与直线AB没有公共点?
当0cm<r<2.4cm或r>4cm时,
⊙C与线段AB没有公共点.
2.Rt△ABC,∠C=90,AC=3cm,BC=4cm,以C为圆心画圆,当半径r为何值时,圆C与线段AB有一个公共点?当半径r为何值时,圆C与线段AB有两个公共点?
A
B
C
A
D
4
5
3
当r=2.4cm或3cm≤r<4cm时,⊙C与线段AB有一个公共点.
当2.4cm<r≤3cm
时,⊙C与线段AB有两公共点.
例2
如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1)
以点C为圆心,当半径为多少时,AB与☉C相切?
(2)
以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?
解:(1)
过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
.O
.O
.O
.O
.O
1.看图判断直线l与☉O的位置关系?
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
?
相交
课堂检测
2.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有(
)
A.
r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
3.
☉O的最大弦长为8,若圆心O到直线l的距离为d=5,则直线l与☉O
.
4.
☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
B
相离
A
解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
5.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
A
24.2
点和圆、直线和圆的位置关系
第二十四章
圆
24.2.2
直线和圆的位置关系
第1课时
直线和圆的位置关系
人教版数学九年级上册
教学目标
1.通过操作、观察,理解直线和圆有三种位置关系。
2.根据圆心到直线的距离与半径之间的数量关系判定直线和圆的位置关系。
3.经历探索直线和圆的位置关系的判定和专题训练,体验从运动观点以及量变到质变的过程理解直线和圆三种位置关系。
教学重点
直线和圆的位置关系的判定。
教学难点
直线和圆的位置关系的判定。
点和圆的位置关系有几种?
d
d>r
用数量关系如何来
判断呢?
(令OP=d
)
知识准备
问题1
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
用定义判断直线与圆的位置关系
探究新知
问题2
请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
0
2
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
反复练习
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
归纳新知
1.直线与圆最多有两个公共点.
2.若直线与圆相交,则直线上的点都在圆上.
3.若A是⊙O上一点,则直线AB与⊙O相切.
4.若C为⊙O外一点,则过点C的直线与⊙O相交或相离.
5.直线a
和⊙O有公共点,则直线a与⊙O相交.
√
×
×
×
×
巩固练习
问题1
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
用数量关系判断直线与圆的位置关系
探究新知
问题2
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
归纳新知
相交
相切
相离
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
2
1
0
巩固练习
例1
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)
r=2cm;(2)
r=2.4cm;
(3)
r=3cm.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
典例精析
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以
(1)当r=2cm时,
有d
>r,
因此⊙C和AB相离.
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,有d=r.
因此⊙C和AB相切.
d
(3)当r=3cm时,有d
d
A
B
C
A
D
4
5
3
变式题:
1.Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心画圆,当半径r为何值时,圆C与直线AB没有公共点?
当0cm<r<2.4cm或r>4cm时,
⊙C与线段AB没有公共点.
2.Rt△ABC,∠C=90,AC=3cm,BC=4cm,以C为圆心画圆,当半径r为何值时,圆C与线段AB有一个公共点?当半径r为何值时,圆C与线段AB有两个公共点?
A
B
C
A
D
4
5
3
当r=2.4cm或3cm≤r<4cm时,⊙C与线段AB有一个公共点.
当2.4cm<r≤3cm
时,⊙C与线段AB有两公共点.
例2
如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1)
以点C为圆心,当半径为多少时,AB与☉C相切?
(2)
以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?
解:(1)
过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
.O
.O
.O
.O
.O
1.看图判断直线l与☉O的位置关系?
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
?
相交
课堂检测
2.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有(
)
A.
r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
3.
☉O的最大弦长为8,若圆心O到直线l的距离为d=5,则直线l与☉O
.
4.
☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
B
相离
A
解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
5.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
A
同课章节目录
