认识三角形

(共29张PPT)
·
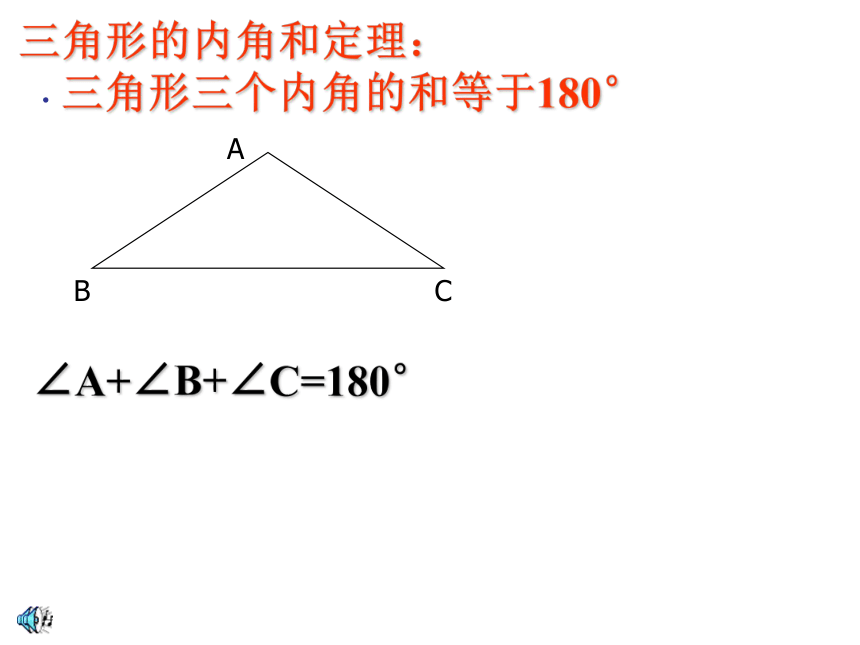
三角形的内角和定理：
三角形三个内角的和等于180°
A
B
C
∠A+∠B+∠C=180°
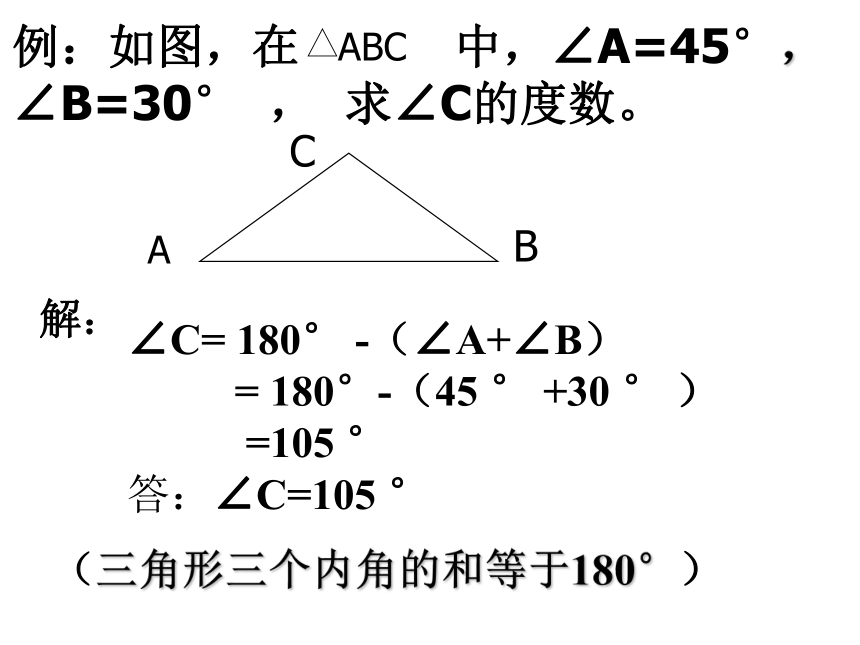
例：如图，在 中，∠A=45°，∠B=30° ， 求∠C的度数。
ABC
C
A
B
解：
（三角形三个内角的和等于180°）
∠C= 180° -（∠A+∠B）
= 180°-（45 ° +30 ° ）
=105 °
答：∠C=105 °
1、 在△ABC中，∠A=45°，∠B=2∠C， 求∠B、 ∠C的度数。
2、在△ABC中，∠A=∠B= 2∠C，
求∠B、 ∠C的度数。
三个内角都是锐角的三角形叫做锐角三角形
有一个内角是直角的三角形叫做直角三角形
有一个内角是钝角的三角形叫做 钝角三角形
三角形按角的大小分类分为：
锐角三角形、直角三角形和
钝角三角形
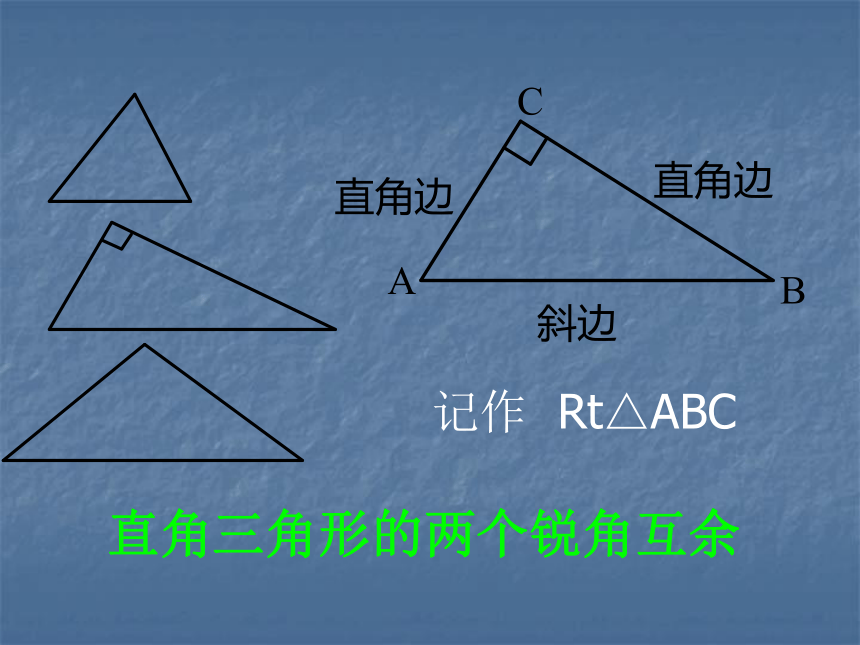
直角三角形的两个锐角互余
记作 Rt△ABC
三角形中至少有一个角不小于（ ）
A．65° B。60°
C．55° D。45°
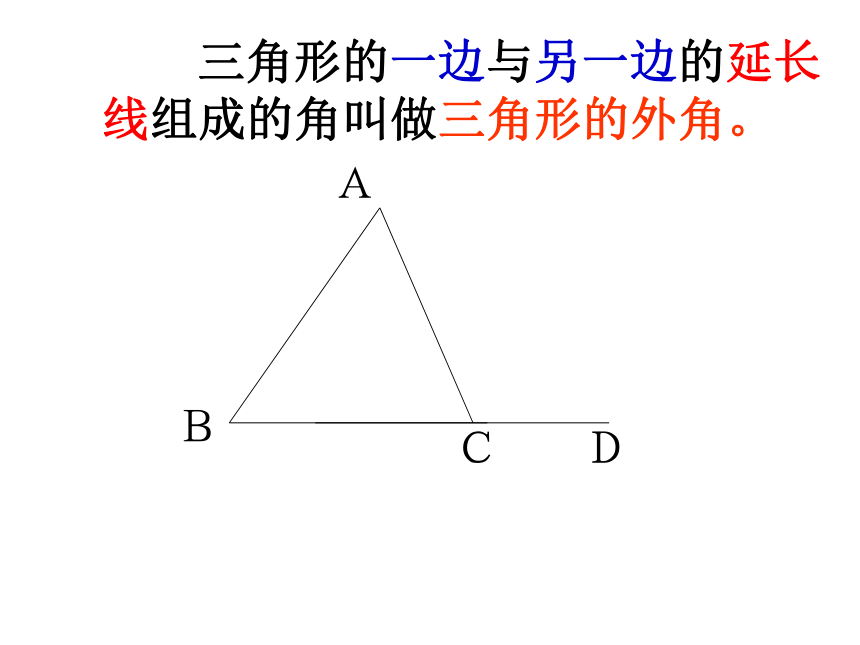
　　三角形的一边与另一边的延长线组成的角叫做三角形的外角。
Ａ
Ｂ
Ｃ
Ｄ
与外角有关的两条数学结论：
1：三角形的一个外角等于
和它不相邻的两个内角的和。
2：三角形的一个外角大于
任何一个和它不相邻的内角。
Ａ
Ｂ
Ｃ
Ｄ
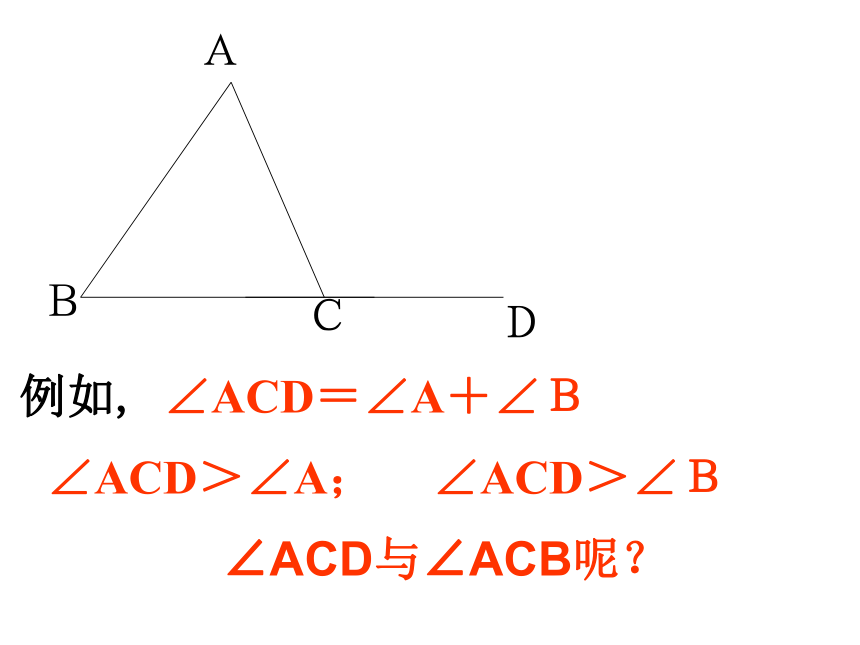
例如, ∠ACD＝∠A＋∠Ｂ
∠ACD＞∠A；
∠ACD＞∠Ｂ
∠ACD与∠ACB呢？
解：∵∠3= ∠1+∠2 （ ）
∠1=∠2（ ）
∴ ∠3= 2∠1 ( )
1
2
3
例：一把椅子的结构如图， ∠1=∠2。当椅面水平时， ∠3=100°，此时∠1的度数是多少？
1
2
3
A
B
C
∴ ∠1 = ∠3
= ×100 ° =50 °
答： ∠1=50 °
例. 已知如图，∠ＢＡＦ、∠ＣＢＤ、
∠ＡＣＥ是△ＡＢＣ的三个外角。
试说明：
∠ＢＡＦ＋∠ＣＢＤ＋∠ＡＣＥ＝３６０0
Ｅ
Ａ
Ｆ
Ｂ
Ｄ
Ｃ
１
２
３
解：
１
Ａ
Ｂ
Ｄ
Ｃ
２
３
Ｆ
∵ ∠ＢＡＦ＝∠２＋∠３
∠ＣＢＤ＝∠１＋∠３
∠ＡＣＥ＝∠１＋∠２
（ ）
∴∠ＢＡＦ＋∠ＣＢＤ＋∠ＡＣＥ
＝（∠２＋∠３）＋（∠１＋∠３）＋（∠１＋∠２） （ ）
＝２（∠１＋∠２＋∠３）
Ｅ
＝２×１８０ （ ）
＝３６０
三角形的外角和定理：
三角形不同顶点处的三个外角的和
等于360
　　每一个三角形都有６个外角．
每一个顶点相对应的外角都有２个．
在三角形的三个外角中，钝角最多有（ ）
A．0个 B。1个
C．2个 D。3个
三角形一个外角小于与它相邻的内角，这个三角形是（ ）
A．直角三角形 B．锐角三角形
C．钝角三角形 D．不能确定
１、在△ABC中∠A：∠B：∠C＝１：２：3，则 △ABC是（ ）
A 锐角三角形 B 直角三角形
C 钝角三角形 D 不能确定
２、已知△ABC中， ∠A∶∠B∶∠C=1∶3∶5，
求∠A、∠B和∠C的度数，
它是什么三角形？
B
３、判断：
（1）一个三角形的三个内角可以都小于60°； 　　　　　　　　（ ）
（2）一个三角形最多只能有一个内角是
钝角或直角； 　　　　　　　（ ）
４、在△ABC中，
（1）∠C=70°，∠A=50°，则∠B= 度
（2）∠B=100°，∠A=∠C，则∠C= 度
√
×
60
40
５、如左图，在 Rt△CDE,　∠C和∠E的关系是 ，其中∠C=55°，则∠E= 度
６、如右图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度；
互余
35
60
30
A
B
C
D
E
看一看：
算一算：
若∠BAC＝55°，∠ B=60 ，
试求∠ ACB, ∠ACD, ∠CAE
的度数．并说出你的理由．
图中哪些角是三角形的内角，
哪些角是三角形的外角？
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
把图中∠1、 ∠2、 ∠3
按由大到小的顺序排列
3
2
1
A
B
C
D
E
已知：如图
BD⊥AC
∠ABD=50°
∠DBC=20°
求∠A和∠C的度数
2、在△ABC中，∠A=80°，∠B=∠C，
则∠C= 。
3、如果△ABC中，∠A∶∠B∶∠C=
2∶3∶5，此三角形按角分类应为 。
4、根据图示求∠α的度数
5、直角三角形的一个锐角为70°，
另一个锐角为 度。
6、如图，在△ABC中，∠A=∠1，
∠2=∠B，∠ABC=∠ACB，
求∠ACB的度数 。
如图：∠A+∠B+∠C+∠D+∠E=