黑龙江省红光农场学校(五四学制)2019-2020学年八年级下学期期末考试数学试题(word版,无答案)
文档属性
| 名称 | 黑龙江省红光农场学校(五四学制)2019-2020学年八年级下学期期末考试数学试题(word版,无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 266.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 00:00:00 | ||
图片预览

文档简介
2019—2020学年度第二学期期末测试
初三年级数学试卷
考生注意:
1.考试时间120分钟
2.全卷共五道大题,总分120分
题号 一 二 三 总分 核分人
16 17 18 19 20 21 22 23
得分
一、选择题(每题 3 分,共 24 分)
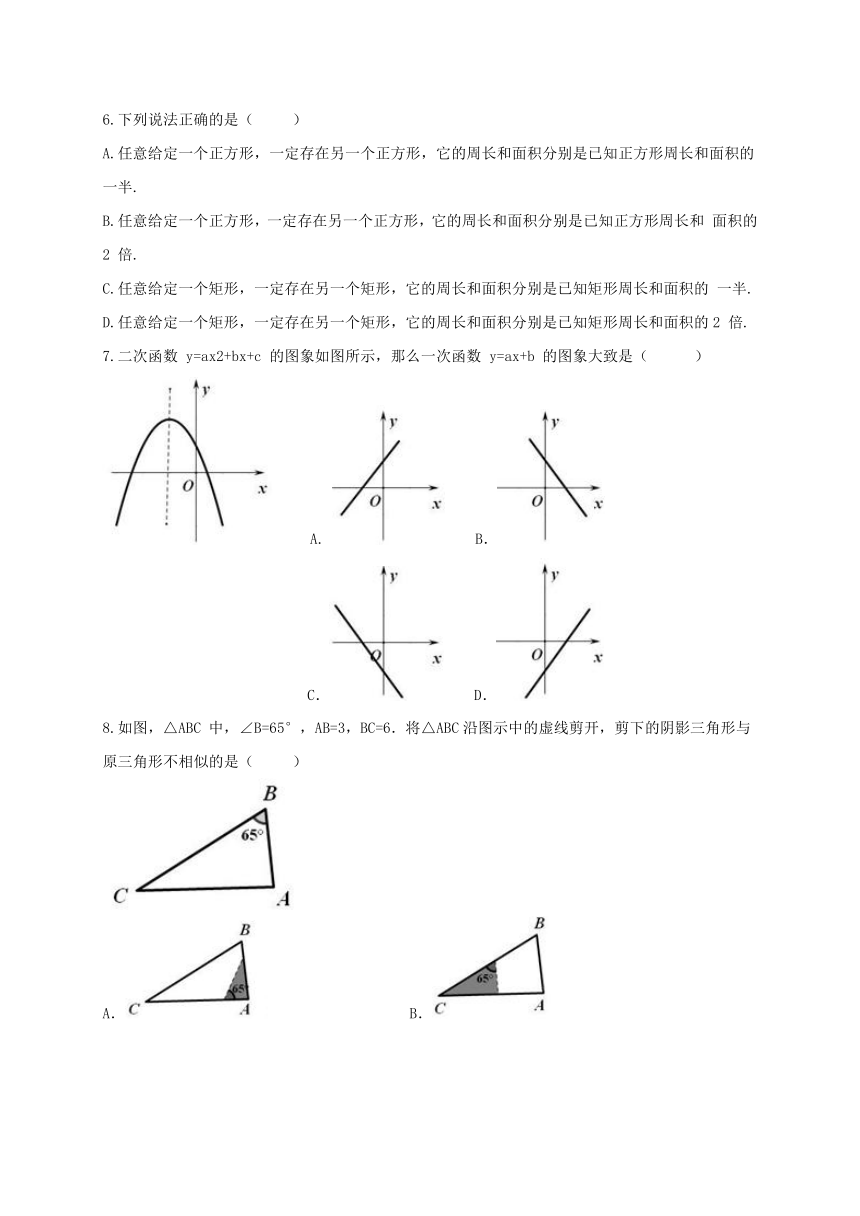
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
2.一元二次方程 x2-4x+4=0 的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
3.下列图形中,是轴对称图形,但不是中心对称图形的是 (? )
4.若双曲线 y=过两点(-1,y1),(-3,y2),则 y1 与 y2 的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.y1 与 y2 大小无法确定
5.如图,在平面直角坐标系中,点 A 的坐标为(4,3),那么 cosα 的值是( )
A. B. C. D.
6.下列说法正确的是( )
A.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的一半.
B.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和 面积的 2 倍.
C.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的 一半.
D.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2 倍.
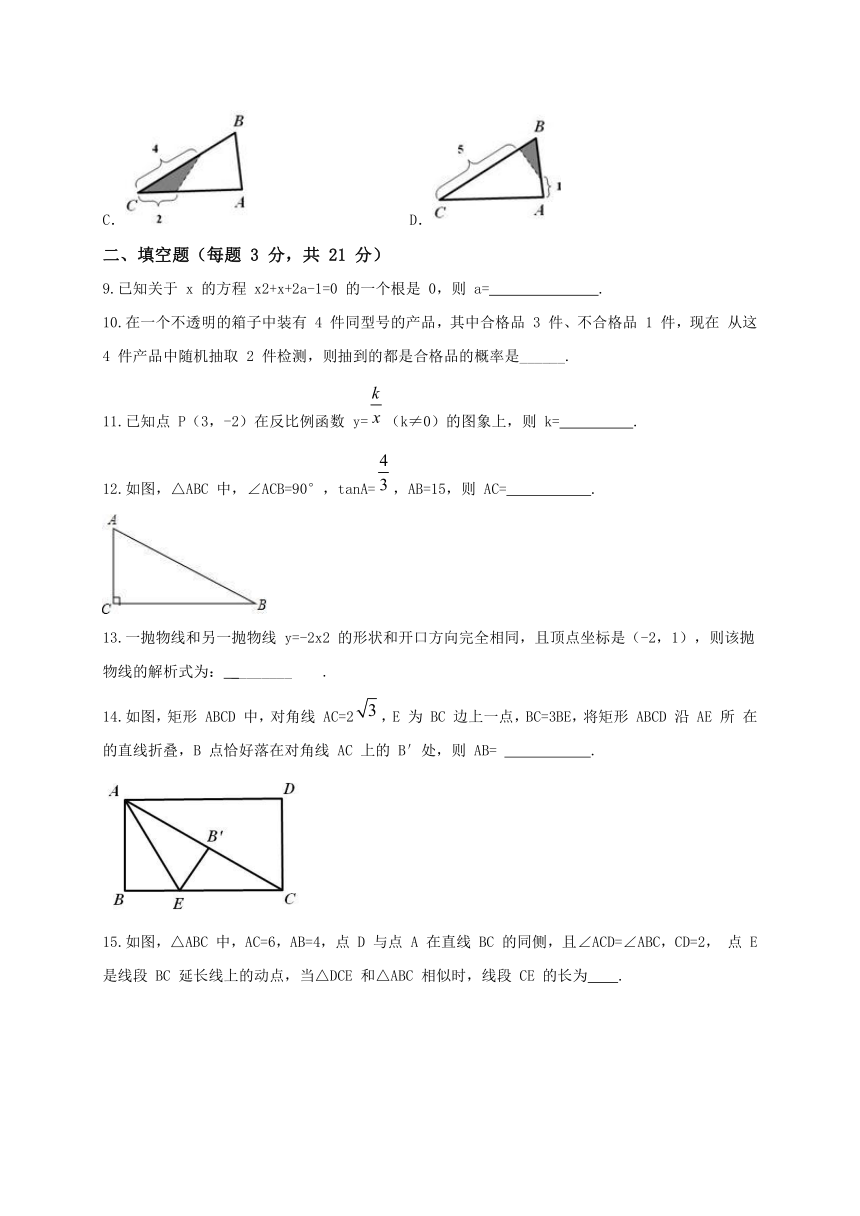
7.二次函数 y=ax2+bx+c 的图象如图所示,那么一次函数 y=ax+b 的图象大致是( )
A. B.
C. D.
8.如图,△ABC 中,∠B=65°,AB=3,BC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
二、填空题(每题 3 分,共 21 分)
9.已知关于 x 的方程 x2+x+2a-1=0 的一个根是 0,则 a= .
10.在一个不透明的箱子中装有 4 件同型号的产品,其中合格品 3 件、不合格品 1 件,现在 从这 4 件产品中随机抽取 2 件检测,则抽到的都是合格品的概率是______.
11.已知点 P(3,-2)在反比例函数 y=(k≠0)的图象上,则 k= .
12.如图,△ABC 中,∠ACB=90°,tanA=,AB=15,则 AC= .
13.一抛物线和另一抛物线 y=-2x2 的形状和开口方向完全相同,且顶点坐标是(-2,1),则该抛物线的解析式为: ________ .
14.如图,矩形 ABCD 中,对角线 AC=2,E 为 BC 边上一点,BC=3BE,将矩形 ABCD 沿 AE 所 在的直线折叠,B 点恰好落在对角线 AC 上的 B′处,则 AB= .
15.如图,△ABC 中,AC=6,AB=4,点 D 与点 A 在直线 BC 的同侧,且∠ACD=∠ABC,CD=2, 点 E 是线段 BC 延长线上的动点,当△DCE 和△ABC 相似时,线段 CE 的长为 .
三、解答题(本题 8 道大题,共 75 分)
16.已知关于 x 的一元二次方程 x2+3x+1-m=0 有两个不相等的实数根.
(1)求 m 的取值范围;
(2)若 m 为负整数,求此时方程的根.
17.在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF, 连接 BE、CF.
(1)求证:△BDF≌△CDE;
(2)若 AB=AC,试判断四边形 BFCE 是怎样的四边形 ,并证明你的结论.
18.甲、乙两个不透明的口袋,甲口袋中装有 3 个分别标有数字 1,2,3 的小球, 乙口袋中装有 2 个分别标有数字 4,5 的小球,它们的形状、大小完全相同,现随机从甲口 袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结 果;
(2)求出两个数字之和能被 3 整除的概率.
如图,小明家在 A 处,门前有一口池塘,隔着池塘有一条公路 L,AB 是 A 到 L的小路.现新修一条路 AC 到公路 L.小明测量出∠ACD=31°,∠ABD=45°,BC=100m.请你 帮小明计算他家到公路 L的距离 AD 的长度?(精确到 1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
如图,在平面直角坐标系 xOy 中,一次函数 y1=ax+b 的图象与反比例函数 y2=的图象相交于点
A(-4,-2),B(m,4).
(1)求反比例函数和一次函数的表达式;
(2)观察图象,写出使得 y1>y2 成立的自变量 x的取值范围.
21.如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
22.如图,AB为⊙O的直径,C.?D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若∠BAC=∠DAC=30度,BC=2,求劣弧BC?的长L
23.某商店原来平均每天可销售某种水果 300 千克,每千克可盈利 6 元,为减少库 存,经市场调查,如果这种水果每千克降价 1 元,则每天可所多售出 30 千克.
(1)设每千克水果降价 x 元,平均每天盈利 y 元,试写出 y 关于 x 的函数表达式;
(2)若要平均每天盈利 1440 元,则每千克应降价多少元?
初三年级数学试卷
考生注意:
1.考试时间120分钟
2.全卷共五道大题,总分120分
题号 一 二 三 总分 核分人
16 17 18 19 20 21 22 23
得分
一、选择题(每题 3 分,共 24 分)
1.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
2.一元二次方程 x2-4x+4=0 的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
3.下列图形中,是轴对称图形,但不是中心对称图形的是 (? )
4.若双曲线 y=过两点(-1,y1),(-3,y2),则 y1 与 y2 的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.y1 与 y2 大小无法确定
5.如图,在平面直角坐标系中,点 A 的坐标为(4,3),那么 cosα 的值是( )
A. B. C. D.
6.下列说法正确的是( )
A.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的一半.
B.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和 面积的 2 倍.
C.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的 一半.
D.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2 倍.
7.二次函数 y=ax2+bx+c 的图象如图所示,那么一次函数 y=ax+b 的图象大致是( )
A. B.
C. D.
8.如图,△ABC 中,∠B=65°,AB=3,BC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
二、填空题(每题 3 分,共 21 分)
9.已知关于 x 的方程 x2+x+2a-1=0 的一个根是 0,则 a= .
10.在一个不透明的箱子中装有 4 件同型号的产品,其中合格品 3 件、不合格品 1 件,现在 从这 4 件产品中随机抽取 2 件检测,则抽到的都是合格品的概率是______.
11.已知点 P(3,-2)在反比例函数 y=(k≠0)的图象上,则 k= .
12.如图,△ABC 中,∠ACB=90°,tanA=,AB=15,则 AC= .
13.一抛物线和另一抛物线 y=-2x2 的形状和开口方向完全相同,且顶点坐标是(-2,1),则该抛物线的解析式为: ________ .
14.如图,矩形 ABCD 中,对角线 AC=2,E 为 BC 边上一点,BC=3BE,将矩形 ABCD 沿 AE 所 在的直线折叠,B 点恰好落在对角线 AC 上的 B′处,则 AB= .
15.如图,△ABC 中,AC=6,AB=4,点 D 与点 A 在直线 BC 的同侧,且∠ACD=∠ABC,CD=2, 点 E 是线段 BC 延长线上的动点,当△DCE 和△ABC 相似时,线段 CE 的长为 .
三、解答题(本题 8 道大题,共 75 分)
16.已知关于 x 的一元二次方程 x2+3x+1-m=0 有两个不相等的实数根.
(1)求 m 的取值范围;
(2)若 m 为负整数,求此时方程的根.
17.在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF, 连接 BE、CF.
(1)求证:△BDF≌△CDE;
(2)若 AB=AC,试判断四边形 BFCE 是怎样的四边形 ,并证明你的结论.
18.甲、乙两个不透明的口袋,甲口袋中装有 3 个分别标有数字 1,2,3 的小球, 乙口袋中装有 2 个分别标有数字 4,5 的小球,它们的形状、大小完全相同,现随机从甲口 袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结 果;
(2)求出两个数字之和能被 3 整除的概率.
如图,小明家在 A 处,门前有一口池塘,隔着池塘有一条公路 L,AB 是 A 到 L的小路.现新修一条路 AC 到公路 L.小明测量出∠ACD=31°,∠ABD=45°,BC=100m.请你 帮小明计算他家到公路 L的距离 AD 的长度?(精确到 1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
如图,在平面直角坐标系 xOy 中,一次函数 y1=ax+b 的图象与反比例函数 y2=的图象相交于点
A(-4,-2),B(m,4).
(1)求反比例函数和一次函数的表达式;
(2)观察图象,写出使得 y1>y2 成立的自变量 x的取值范围.
21.如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
22.如图,AB为⊙O的直径,C.?D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若∠BAC=∠DAC=30度,BC=2,求劣弧BC?的长L
23.某商店原来平均每天可销售某种水果 300 千克,每千克可盈利 6 元,为减少库 存,经市场调查,如果这种水果每千克降价 1 元,则每天可所多售出 30 千克.
(1)设每千克水果降价 x 元,平均每天盈利 y 元,试写出 y 关于 x 的函数表达式;
(2)若要平均每天盈利 1440 元,则每千克应降价多少元?
同课章节目录
