人教版七年级下册 5.1.1相交线 课件(20张PPT)
文档属性
| 名称 | 人教版七年级下册 5.1.1相交线 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 17.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 23:24:06 | ||
图片预览



文档简介
(共20张PPT)
●
相交
平行
5.1.1
相交线
生活中的相交直线
一、导入新课
生活中的相交直线
有一个公共点的两条直线形成相交直线.
相交线的定义:
●
O
1
2
3
4
二线四角图
一、知识要点
A
B
C
D
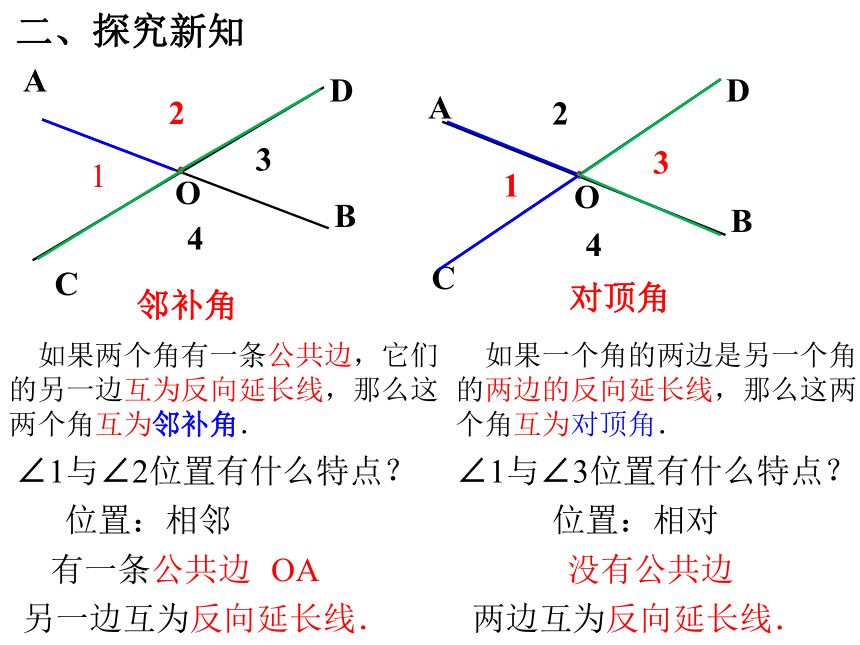
两条直线的位置关系:直线AB与直线CD相交于点O
问:(1)两条相交直线形成的小于平角的角有几个?
答:∠1,∠2,∠3,∠4
(2)看看这四个角有什么关系?
二、探究新知
位置:相邻
∠1与∠2位置有什么特点?
有一条公共边
另一边互为反向延长线.
OA
邻补角
∠1与∠3位置有什么特点?
位置:相对
两边互为反向延长线.
对顶角
没有公共边
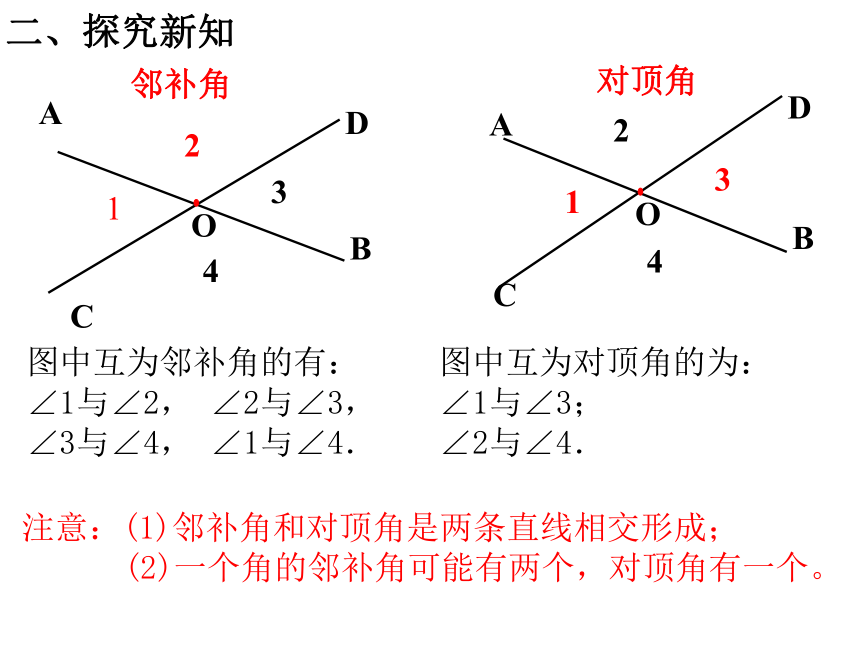
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
二、探究新知
邻补角
对顶角
图中互为邻补角的有:
∠1与∠2,
∠2与∠3,
∠3与∠4,
∠1与∠4.
图中互为对顶角的为:
∠1与∠3;
∠2与∠4.
注意:(1)邻补角和对顶角是两条直线相交形成;
(2)一个角的邻补角可能有两个,对顶角有一个。
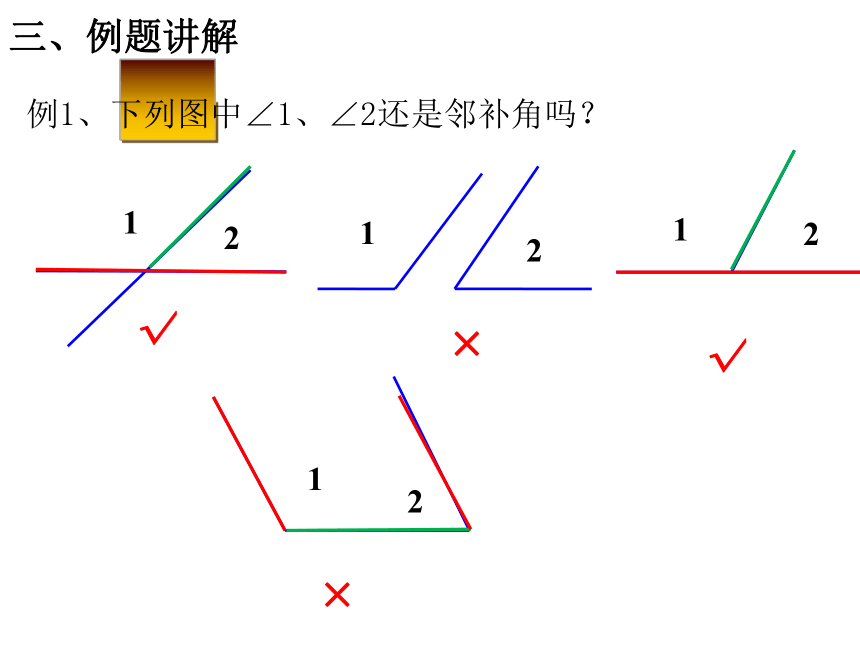
例1、下列图中∠1、∠2还是邻补角吗?
三、例题讲解
1
2
√
×
√
×
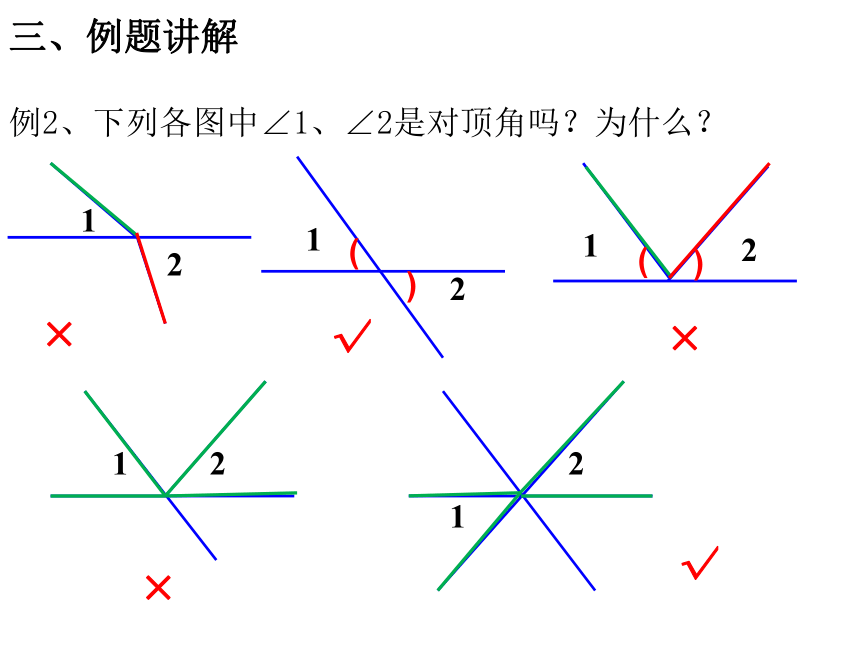
例2、下列各图中∠1、∠2是对顶角吗?为什么?
三、例题讲解
1
2
1
2
)
(
(
)
×
×
×
√
√
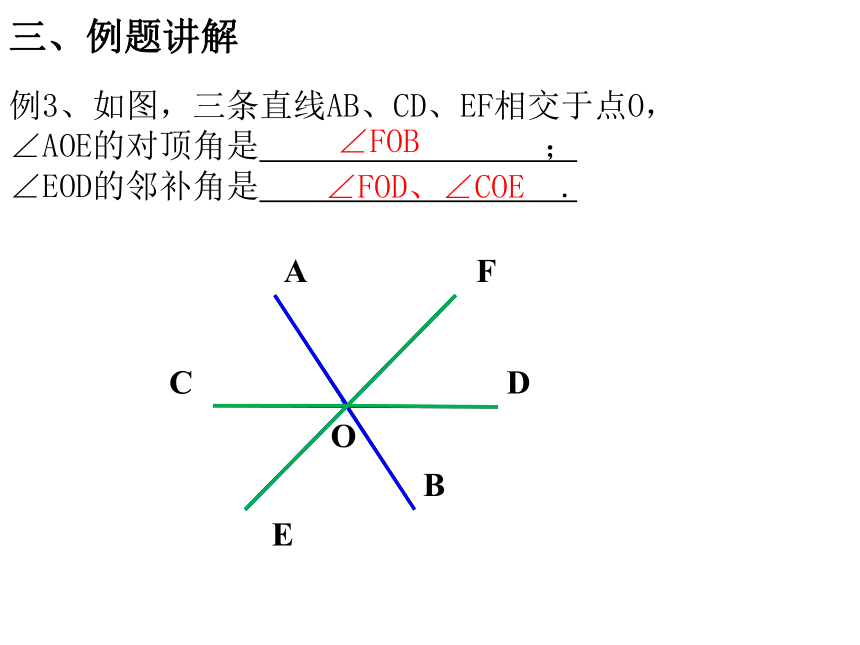
例3、如图,三条直线AB、CD、EF相交于点O,
∠AOE的对顶角是
;
∠EOD的邻补角是
.
三、例题讲解
A
B
C
D
E
F
O
∠FOB
∠FOD、∠COE
三、例题讲解
例4、请分别画出∠1的对顶角和∠2的邻补角.
1
2
四、
邻补角
数量关系:互补
邻补角、对顶角的性质
对顶角
猜想:∠1=∠3
证明:∵∠1+∠2=180°
∠3+∠2=180°
(邻补角的定义)
∴∠1=∠3
(同角的补角相等)
同理,∠2=∠4
对顶角相等
四、
邻补角、对顶角的性质
四、
邻补角
对顶角
数量关系:互补
数量关系:相等
性质:邻补角互补,对顶角相等
邻补角、对顶角的性质
例1、判断题
(1)一对邻补角一定互补.
(2)一对互补的角一定是邻补角.
五、例题讲解
√
×
(3)有公共顶点且相等的两个角是对顶角.
(4)两条直线相交,有两组对顶角.
×
√
例2、如图所示,直线m,n相交于点O,∠1=60°,
求∠2,∠3,∠4的度数.
解:由邻补角的定义,可得:
∠2=180°-∠1
=180°-60°
=120°
五、例题讲解
O
由对顶角相等,可得:
∠3=∠1=60°,
∠4=∠2=120°.
例2、如图所示,直线m,n相交于点O,
变式1:若∠1+∠3=80°,求各个角的度数.
解:由对顶角相等,设∠1=x,∠3=x
五、例题讲解
O
即∠1=∠3=40°
∵∠1+∠3=80°
∴x+x=80°
解得x=40°
由邻补角定义得
∠2=180°?∠1=180°?40°=140°
由对顶角相等∠4=∠2=140°
例2、如图所示,直线m,n相交于点O,
变式2:若∠2是∠1的3.5倍,求各个角的度数.
解:设∠1=x,∠2=3.5x
五、例题讲解
O
即∠1=40°,∠2=140°
∵∠1+∠2=180°
∴x+3.5x=180°
解得x=40°
由对顶角相等∠3=∠1=40°,∠4=∠2=140°
例2、如图所示,直线m,n相交于点O,
变式3:若∠1:∠2=2:7,求各个角的度数.
解:设∠1=2x,∠2=7x
五、例题讲解
O
即∠1=40°,∠2=140°
∵∠1+∠2=180°
∴2x+x=180°
解得x=20°
由对顶角相等∠3=∠1=40°,∠4=∠2=140°
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对邻补角有四对
①有无公共边
课堂小结
角的
名称
特
征
性
质
相
同
点
不
同
点
对
顶
角
邻
补
角
4.直线AB、CD交于点O,OP是∠BOC的平分线,已知∠AOC=54°.求∠BOP的度数.
●
相交
平行
5.1.1
相交线
生活中的相交直线
一、导入新课
生活中的相交直线
有一个公共点的两条直线形成相交直线.
相交线的定义:
●
O
1
2
3
4
二线四角图
一、知识要点
A
B
C
D
两条直线的位置关系:直线AB与直线CD相交于点O
问:(1)两条相交直线形成的小于平角的角有几个?
答:∠1,∠2,∠3,∠4
(2)看看这四个角有什么关系?
二、探究新知
位置:相邻
∠1与∠2位置有什么特点?
有一条公共边
另一边互为反向延长线.
OA
邻补角
∠1与∠3位置有什么特点?
位置:相对
两边互为反向延长线.
对顶角
没有公共边
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
二、探究新知
邻补角
对顶角
图中互为邻补角的有:
∠1与∠2,
∠2与∠3,
∠3与∠4,
∠1与∠4.
图中互为对顶角的为:
∠1与∠3;
∠2与∠4.
注意:(1)邻补角和对顶角是两条直线相交形成;
(2)一个角的邻补角可能有两个,对顶角有一个。
例1、下列图中∠1、∠2还是邻补角吗?
三、例题讲解
1
2
√
×
√
×
例2、下列各图中∠1、∠2是对顶角吗?为什么?
三、例题讲解
1
2
1
2
)
(
(
)
×
×
×
√
√
例3、如图,三条直线AB、CD、EF相交于点O,
∠AOE的对顶角是
;
∠EOD的邻补角是
.
三、例题讲解
A
B
C
D
E
F
O
∠FOB
∠FOD、∠COE
三、例题讲解
例4、请分别画出∠1的对顶角和∠2的邻补角.
1
2
四、
邻补角
数量关系:互补
邻补角、对顶角的性质
对顶角
猜想:∠1=∠3
证明:∵∠1+∠2=180°
∠3+∠2=180°
(邻补角的定义)
∴∠1=∠3
(同角的补角相等)
同理,∠2=∠4
对顶角相等
四、
邻补角、对顶角的性质
四、
邻补角
对顶角
数量关系:互补
数量关系:相等
性质:邻补角互补,对顶角相等
邻补角、对顶角的性质
例1、判断题
(1)一对邻补角一定互补.
(2)一对互补的角一定是邻补角.
五、例题讲解
√
×
(3)有公共顶点且相等的两个角是对顶角.
(4)两条直线相交,有两组对顶角.
×
√
例2、如图所示,直线m,n相交于点O,∠1=60°,
求∠2,∠3,∠4的度数.
解:由邻补角的定义,可得:
∠2=180°-∠1
=180°-60°
=120°
五、例题讲解
O
由对顶角相等,可得:
∠3=∠1=60°,
∠4=∠2=120°.
例2、如图所示,直线m,n相交于点O,
变式1:若∠1+∠3=80°,求各个角的度数.
解:由对顶角相等,设∠1=x,∠3=x
五、例题讲解
O
即∠1=∠3=40°
∵∠1+∠3=80°
∴x+x=80°
解得x=40°
由邻补角定义得
∠2=180°?∠1=180°?40°=140°
由对顶角相等∠4=∠2=140°
例2、如图所示,直线m,n相交于点O,
变式2:若∠2是∠1的3.5倍,求各个角的度数.
解:设∠1=x,∠2=3.5x
五、例题讲解
O
即∠1=40°,∠2=140°
∵∠1+∠2=180°
∴x+3.5x=180°
解得x=40°
由对顶角相等∠3=∠1=40°,∠4=∠2=140°
例2、如图所示,直线m,n相交于点O,
变式3:若∠1:∠2=2:7,求各个角的度数.
解:设∠1=2x,∠2=7x
五、例题讲解
O
即∠1=40°,∠2=140°
∵∠1+∠2=180°
∴2x+x=180°
解得x=20°
由对顶角相等∠3=∠1=40°,∠4=∠2=140°
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对邻补角有四对
①有无公共边
课堂小结
角的
名称
特
征
性
质
相
同
点
不
同
点
对
顶
角
邻
补
角
4.直线AB、CD交于点O,OP是∠BOC的平分线,已知∠AOC=54°.求∠BOP的度数.
