上海市浦东新区2018-2019学年七年级(五四学制)下学期期末考试数学试题(图片版,含答案)
文档属性
| 名称 | 上海市浦东新区2018-2019学年七年级(五四学制)下学期期末考试数学试题(图片版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 00:00:00 | ||
图片预览


文档简介
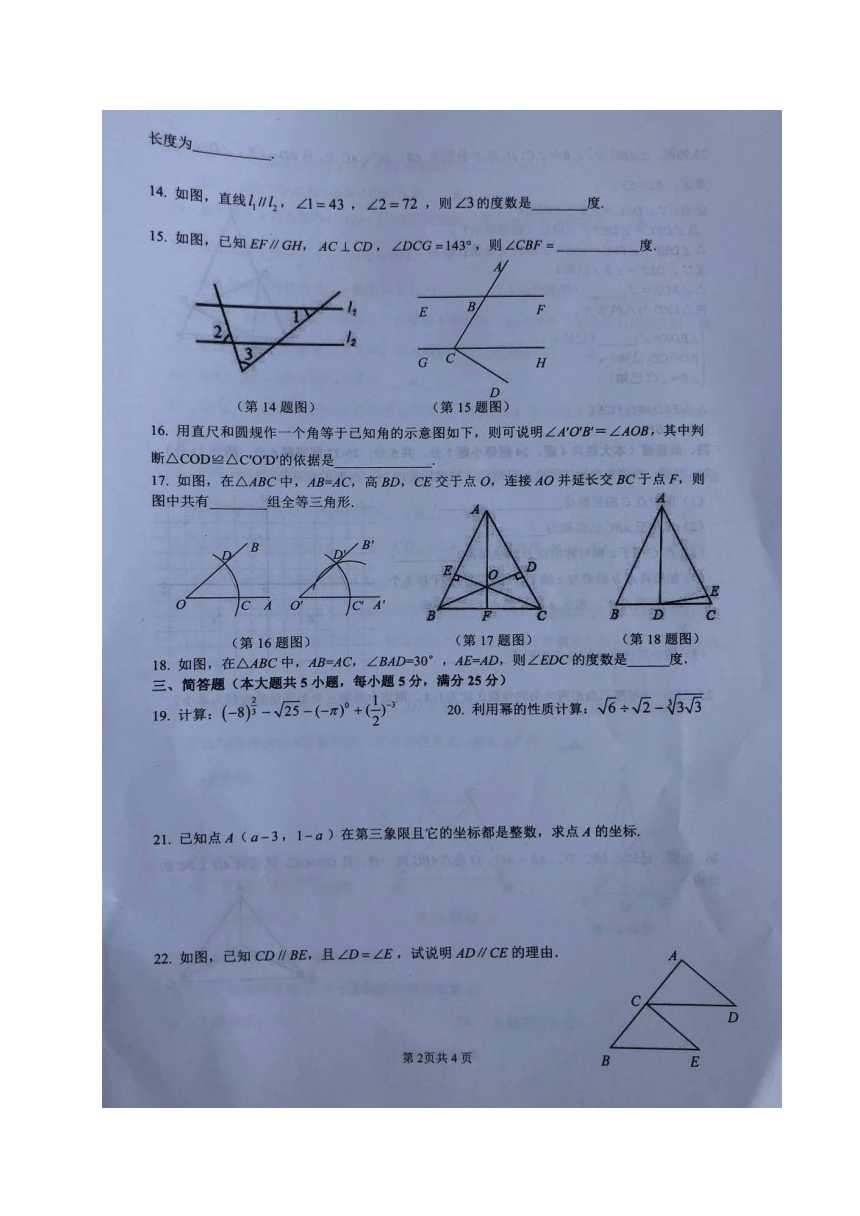
长度为
14.如图,直线l1∥l2,∠1=43,∠2=72,则∠3的度数是度
15.如图,已知EF∥GH,AC⊥CD,∠DCG=143°,则∠CBF=
度
(第14题图)
(第15题图)
16.用直尺和圆规作一个角等于已知角的示意图如下,则可说明∠AOB=∠AOB,其中判
断△COD≌△COD的依据是
小4,
本),四
17.如图,在△ABC中,AB=AC,高BD,CE交于点O,连接AO并延长交BC于点F,则
图中共有
组全等三角形
A
B
B
C
A
O
(第16题图)
(第17题图)
(第18题图)
18.如图,在△ABC中,AB=AC,∠BAD=30°,AE=AD,则∠EDC的度数是
度
三、简答题(本大题共5小题,每小题5分,满分25分)
19.计算:(-8)
)9+(
20.利用幂的性质计算:6÷√互-3
21.已知点A(a-3,1-a)在第三象限且它的坐标都是整数,求点A的坐标
22.如图,已知CD∥BE,且∠D=∠E,试说明AD∥CE的理由
第2页共4页
23.如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B
求证:ED=EF
证明:∵∠DEC=∠B+∠BDE(
且∠DEC=∠DEF+∠FEC(如图所示)
∴∠DEF十∠FEC=∠B+∠BDE(等量代换)
又∵∠DEF=∠B(已知),
∴∠BDE=∠
(等式性质)
在△EBD与△FCE中,
∠BDE=∠
(已证),
BD=CE(已知)
∠B=∠C(已知),
∴△EBD≌△FCE(
ED=EFO
四、解答题(本大题共4题,24题每小题1分,共5分,25-27题每题6分,满分23分)
4.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(-3,-2)
(1)图中点C的坐标是
(2)三角形ABC的面积为
(3)点C关于x轴对称的点D的坐标是
(4)如果将点B沿着与x轴平行的方向向右平移3个
单位得到点B,那么A、B两点之间的距离
是
(5)图中四边形ABCD的面积是
25已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为多少?
26.如图,已知△ABC中,AB=AC,O是△ABC内一点,且OB=OC,试说明AO⊥BC的
理由
BA
第3页共4页
27公园里有一条“z”字形道路ABCD,如图所示,其中AB∥CD,在AB,CD,BC三段路
旁各有一只小石凳E,F,M,且BE=CF,M是BC的中点,试说明三只石凳E,F,M恰
好在一条直线上.(提示:可通过证明∠EMF=180°)
A
五、能力题(满分8分)
28.在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D
点旋转,它的两边分别交AC和CB(或它们的延长线)于E,F.
(1)当DE⊥AC于E时(如图1),可得S△DE+ScgF=
(2)当DE与AC不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予
证明;若不成立,请直接给出SDEF,SCEF,S△ABC的关系
(3)当点E在AC延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给
予证明;若不成立,请直接给出S△DEF,S△CEF,S△ABC的关系
A
图2
图3
4页共4页
14.如图,直线l1∥l2,∠1=43,∠2=72,则∠3的度数是度
15.如图,已知EF∥GH,AC⊥CD,∠DCG=143°,则∠CBF=
度
(第14题图)
(第15题图)
16.用直尺和圆规作一个角等于已知角的示意图如下,则可说明∠AOB=∠AOB,其中判
断△COD≌△COD的依据是
小4,
本),四
17.如图,在△ABC中,AB=AC,高BD,CE交于点O,连接AO并延长交BC于点F,则
图中共有
组全等三角形
A
B
B
C
A
O
(第16题图)
(第17题图)
(第18题图)
18.如图,在△ABC中,AB=AC,∠BAD=30°,AE=AD,则∠EDC的度数是
度
三、简答题(本大题共5小题,每小题5分,满分25分)
19.计算:(-8)
)9+(
20.利用幂的性质计算:6÷√互-3
21.已知点A(a-3,1-a)在第三象限且它的坐标都是整数,求点A的坐标
22.如图,已知CD∥BE,且∠D=∠E,试说明AD∥CE的理由
第2页共4页
23.如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B
求证:ED=EF
证明:∵∠DEC=∠B+∠BDE(
且∠DEC=∠DEF+∠FEC(如图所示)
∴∠DEF十∠FEC=∠B+∠BDE(等量代换)
又∵∠DEF=∠B(已知),
∴∠BDE=∠
(等式性质)
在△EBD与△FCE中,
∠BDE=∠
(已证),
BD=CE(已知)
∠B=∠C(已知),
∴△EBD≌△FCE(
ED=EFO
四、解答题(本大题共4题,24题每小题1分,共5分,25-27题每题6分,满分23分)
4.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(-3,-2)
(1)图中点C的坐标是
(2)三角形ABC的面积为
(3)点C关于x轴对称的点D的坐标是
(4)如果将点B沿着与x轴平行的方向向右平移3个
单位得到点B,那么A、B两点之间的距离
是
(5)图中四边形ABCD的面积是
25已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为多少?
26.如图,已知△ABC中,AB=AC,O是△ABC内一点,且OB=OC,试说明AO⊥BC的
理由
BA
第3页共4页
27公园里有一条“z”字形道路ABCD,如图所示,其中AB∥CD,在AB,CD,BC三段路
旁各有一只小石凳E,F,M,且BE=CF,M是BC的中点,试说明三只石凳E,F,M恰
好在一条直线上.(提示:可通过证明∠EMF=180°)
A
五、能力题(满分8分)
28.在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D
点旋转,它的两边分别交AC和CB(或它们的延长线)于E,F.
(1)当DE⊥AC于E时(如图1),可得S△DE+ScgF=
(2)当DE与AC不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予
证明;若不成立,请直接给出SDEF,SCEF,S△ABC的关系
(3)当点E在AC延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给
予证明;若不成立,请直接给出S△DEF,S△CEF,S△ABC的关系
A
图2
图3
4页共4页
同课章节目录
