上海市青浦区2018-2019学年第二学期七年级数学期末试卷(可编辑PDF版,含答案)
文档属性
| 名称 | 上海市青浦区2018-2019学年第二学期七年级数学期末试卷(可编辑PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-22 15:11:22 | ||
图片预览


文档简介
青浦区 2018 学年第二学期七年级数学期末测试
(时间90分钟,满分100分)
一、填空题(每题2分,满分28分)
1.16的平方根等于 .
2.计算:5 ?32 ?______________.
3.比较大小:? 15________-4.(填“>”、“=”或“<”)
1
4.计算:83 ?__________.
5.计算: 40? 10= .
1
6.用幂的形式表示: = .
3 2
5
?
7.如图,直线AB、CD相交于点O,OE平分?BOC.如果?BOE ?65 ,那
么?AOC= 度.
8.如图,直线c与 ,ba 都相交, a//b,如果?2? ?110 ,那么?1= 度.
9.如果点P在第二象限,且点P到x轴的距离是3,到y轴的距离是5,那么点P
的坐标是 .
10.已知△ ABC 的两边 a ?8 , b?2 ,那么第三条边 c 的长度的范围
是 .
? ?
11.如图3,在Rt△ABC中,?ABC ?90 ,BD是斜边AC 上的高.如果?1?54 ,
那 么 ?C =
度.
12.如图 4,已知 AD//BC ,AC 与 BD 相交于点 O.请写出图中面积相等的一对三角形:
(只要写出一对即可).
(第13题图)
13.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),
那么图中∠α= 度.
?
14.如果一个等腰三角形其中一腰上的高与另一腰的夹角是30 ,那么这个等腰三角形的顶角等于
度.
1
二、选择题(每题3分,满分12分) 22
15.下列各数中: 3
0、?2、 8、 、?、0.3737737773?(它的位数无限且相邻两个“3”之间“7”
7
的个数依次加1个),无理数有……………………………………………………………………………( ).
(A) 1个; (B) 2个; (C) 3个; (D) 4个.
16.下列说法中正确的是……………………………………………………………………………………( )
(A)无限不循环小数是无理数;
(B)一个无理数的平方一定是有理数;
(C)无理数包括正无理数、负无理数和零;
(D)两个无理数的和、差、积、商仍是无理数.
17.将一直角三角板与两边平行的纸条如图所示放置,下列结论: (第17题图)
(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,
其中正确的个数是…………………………………………( )
(A)1; (B)2; (C)3; (D)4. M A
G
E
18.如图,AOB是一钢架,且∠AOB=10°,为加固钢架,需要在其内部添加 O F H B
一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,那么最多能添加 (第18题图)
这样钢管的根数为……………………………………………( )
(A)6; (B)7; (C)8; (D)9.
三、解答题(第19、20题每题5分,第21、22题每题6分,满分22分)
19.计算: .
?5?25 5??
20.利用幂的运算性质进行计算:3 6
?? 32816 .
21.画图(不要求写画法,但需保留作图痕迹,并写出结论).
(1)画△ABC,使AB ?4cm,BC ?2cm,AC ?3cm;
(2)画△ABC边AC上的中线BD.
2
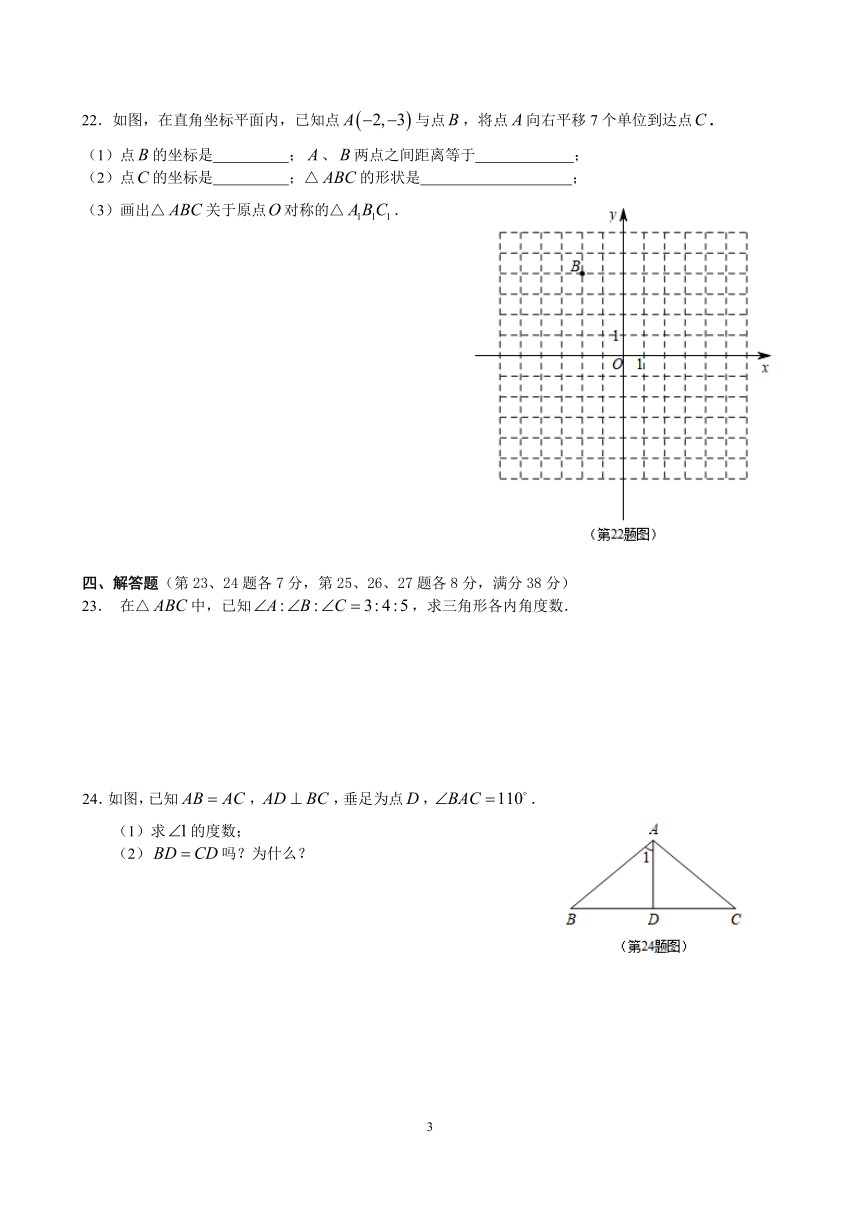
22.如图,在直角坐标平面内,已知点A??2,3? ?与点B,将点A向右平移7个单位到达点C.
(1)点B的坐标是 ;A、B两点之间距离等于 ;
(2)点C的坐标是 ;△ABC的形状是 ;
(3)画出△ABC关于原点O对称的△A1BC11.
四、解答题(第23、24题各7分,第25、26、27题各8分,满分38分)
23. 在△ABC中,已知?A:???BC: 3:4:5,求三角形各内角度数.
?
24.如图,已知AB ? AC ,AD ? BC ,垂足为点D,?BAC ?110 .
(1)求?1的度数;
(2)BD ?CD吗?为什么?
3
25.如图,点A、B、C、D在一条直线上.如果AC ? BD,BE ?CF ,且BE//CF,那么AE//DF .为
什么?
解:因为BE//CF(已知),
所以?EBC FCB?? ( ).
? ?
因为? ?? ?EBC EBA 180 ,? ?? ?FCB FCD 180 (平角的意义),
所以 ( ).
因为AC ? BD(已知),
所以AC?BCBDBC? ? (等式性质),
即 .
(完成以下说理过程)
26.已知:如图,△ABC是等边三角形,点D、E分别在边AB、BC的延长线上,且AD = BE,联结DC、
AE.
(1)试说明△BCD≌△ACE的理由; A
(2)如果BE = 2AB,求∠BAE的度数.
B E
C
D
(第26题图)
27.已知点A (0,4)、B(3,0),AB=5,建立直角坐标系并在直角坐标系中作出点A、B.若点C(与A、
B不重合)在坐标轴上,且AC=AB或BC=AB,求所有符合条件的点C的坐标.
4
青浦区2018学年第二学期七年级数学期末测试
参考答案与评分意见
一、填空题(每题2分,满分28分)
?2
? ?
1.?4; 2.-2; 3.>; 4.2; 5.20; 6.5 3; 7.50 ; 8.70 ; 9.? ??5,3 ;
?
10.10>c>6; 11.54 ; 12.△ABD与△ADC或△DCO与△ABO或△ABC与△DBC;
? ?
13.75°; 14.60 或120 ;
二、选择题(每题3分,满分共12分)
15.B; 16.A; 17.D; 18.C.
三、解答题(第19、20题各5分,第21、22题各6分,满分22分)
2
19.解:原式? ? ????5 25 5? …………………………………………………(1分)
?? ??
2
? ? 1
? ? ???5 25 …………………………………………………(1分)
?? ?? 5
2 1 1
? ? ? ? ………………………………………………( 分)
??5 25 1
5 5
? ?5 2…………………………………………………………………(2分)
【说明】没有过程,直接得结论扣2分.
4 3 5
20. 解:原式= 3 2 ?? 222 6……………………………………………………………………(3分)
4 3?? 5
=23 2 6…………………………………………………………………………(2分)
8
= 3 3
? 442 .……………………………………………………………………(1分)
21.(1)画图正确2分,标注字母正确1分,结论1分;
(2)画图正确1分,标注字母正确1分.
22.(1)? ??2,4 ,7;……………………………………………………………(1+1)分
(2)? ?5,3? ,等腰直角三角形;…………………………………………(1+1)分
(3)画图正确1分,标注字母正确1分.
四、解答题(第23、24题各7分,第25、26、27题各8分,满分38分)
1
23.解:根据题意:设?A 、?B 、?C的度数分别为3x、4x、5x.……(1分)
因为?A 、?B 、?C是△ABC的三个内角(已知),
? ?
所以??????A B C 180 (三角形的内角和等于180 ),……………(1分)
即 3xxx???45180.…………………………………………………(2分)
解得 x?15.……………………………………………………………(2分)
? ? ?
所以 ??A 45 ,??B 60 ,??C 75 .………………………………(1分)
24.解:(1) 因为ABAC? (已知),
所以△ABC是等腰三角形.
由ADBC? (已知),
1
得???1 BAC(等腰三角形的三线合一).……………………………(3分)
2
?
由? ?BAC 110 (已知),
1
? ?
得??? ?1 11055 .……………………………………………………(2分)
2
(2)因为△ABC是等腰三角形,ADBC? (已知),
所以BDCD? (等腰三角形的三线合一).……………………………(2分)
【说明】在用“等腰三角形的三线合一”性质时,前面两个条件有漏写的,要扣1分.
25.解: 两直线平行,内错角相等…………………………………………………(1分)
? ??EBA FCD…………………………………………………………(1分)
等角的补角相等……………………………………………………………(1分)
ABCD? .………………………………………………………………(1分)
在△ABE和△DCF中,
?ABCD? ,
?
?? ??ABE DCF, ……………………………………………………(1分)
??BECF? (已知),
所以△ABE≌△DCF(S.A.S),……………………………………(1分)
得???A D(全等三角形的对应角相等),…………………………(1分)
所以AEDF// (内错角相等,两直线平行).…………………………(1分)
26..解:(1)因为 △ABC是等边三角形,(已知)
所以 AB = BC = AC,
? ?? ??ABC ACB 60 .(等边三角形的三边相等,每一个内角等于60°)
所以 ∠DBC =∠ECA.(等角的补角相等)…………………………(1分)
2
因为 AD = BE,(已知)
所以 AD -AB = BE -BC.(等式性质)
即得 BD = CE.………………………………………………………(1分)
在△BCD和△ACE中,
?BCCA? ,
??? ??DBC ECA,
??BDCE? ,
所以 △BCD≌△ACE(S.A.S).…………………………………(2分)
(2)因为 BE = 2BC,(已知)
所以 BC = CE.
因为 AC = BC,(已证)
所以 AC = CE.(等量代换)
所以 ∠CAE =∠E.(等边对等角)…………………………………(2分)
因为 ∠ACB =∠CAE +∠E = 60°,(三角形的一个外角等于其不相邻的两个内角的和)
所以 ∠E = 30°.
因为 ∠ABE +∠E +∠BAE = 180°,(三角形三个内角的和等于180°)
所以 ∠BAE =180° -∠ABE -∠E = 90°.……………………………(2分)
27.解:正确画出坐标系…………(1分)
正确画出点A、B …………(1分)
以A为圆心,AB为半径画弧交坐标轴于点
C1 ? ,)03( C2 ,)90( C3 ,? )10( …………(3分)
以B为圆心,AB为半径画弧交坐标轴于点
C4 ? ,)02( C5 ,)08( C6 ,? )40( …………(3分)
3
(时间90分钟,满分100分)
一、填空题(每题2分,满分28分)
1.16的平方根等于 .
2.计算:5 ?32 ?______________.
3.比较大小:? 15________-4.(填“>”、“=”或“<”)
1
4.计算:83 ?__________.
5.计算: 40? 10= .
1
6.用幂的形式表示: = .
3 2
5
?
7.如图,直线AB、CD相交于点O,OE平分?BOC.如果?BOE ?65 ,那
么?AOC= 度.
8.如图,直线c与 ,ba 都相交, a//b,如果?2? ?110 ,那么?1= 度.
9.如果点P在第二象限,且点P到x轴的距离是3,到y轴的距离是5,那么点P
的坐标是 .
10.已知△ ABC 的两边 a ?8 , b?2 ,那么第三条边 c 的长度的范围
是 .
? ?
11.如图3,在Rt△ABC中,?ABC ?90 ,BD是斜边AC 上的高.如果?1?54 ,
那 么 ?C =
度.
12.如图 4,已知 AD//BC ,AC 与 BD 相交于点 O.请写出图中面积相等的一对三角形:
(只要写出一对即可).
(第13题图)
13.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),
那么图中∠α= 度.
?
14.如果一个等腰三角形其中一腰上的高与另一腰的夹角是30 ,那么这个等腰三角形的顶角等于
度.
1
二、选择题(每题3分,满分12分) 22
15.下列各数中: 3
0、?2、 8、 、?、0.3737737773?(它的位数无限且相邻两个“3”之间“7”
7
的个数依次加1个),无理数有……………………………………………………………………………( ).
(A) 1个; (B) 2个; (C) 3个; (D) 4个.
16.下列说法中正确的是……………………………………………………………………………………( )
(A)无限不循环小数是无理数;
(B)一个无理数的平方一定是有理数;
(C)无理数包括正无理数、负无理数和零;
(D)两个无理数的和、差、积、商仍是无理数.
17.将一直角三角板与两边平行的纸条如图所示放置,下列结论: (第17题图)
(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,
其中正确的个数是…………………………………………( )
(A)1; (B)2; (C)3; (D)4. M A
G
E
18.如图,AOB是一钢架,且∠AOB=10°,为加固钢架,需要在其内部添加 O F H B
一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,那么最多能添加 (第18题图)
这样钢管的根数为……………………………………………( )
(A)6; (B)7; (C)8; (D)9.
三、解答题(第19、20题每题5分,第21、22题每题6分,满分22分)
19.计算: .
?5?25 5??
20.利用幂的运算性质进行计算:3 6
?? 32816 .
21.画图(不要求写画法,但需保留作图痕迹,并写出结论).
(1)画△ABC,使AB ?4cm,BC ?2cm,AC ?3cm;
(2)画△ABC边AC上的中线BD.
2
22.如图,在直角坐标平面内,已知点A??2,3? ?与点B,将点A向右平移7个单位到达点C.
(1)点B的坐标是 ;A、B两点之间距离等于 ;
(2)点C的坐标是 ;△ABC的形状是 ;
(3)画出△ABC关于原点O对称的△A1BC11.
四、解答题(第23、24题各7分,第25、26、27题各8分,满分38分)
23. 在△ABC中,已知?A:???BC: 3:4:5,求三角形各内角度数.
?
24.如图,已知AB ? AC ,AD ? BC ,垂足为点D,?BAC ?110 .
(1)求?1的度数;
(2)BD ?CD吗?为什么?
3
25.如图,点A、B、C、D在一条直线上.如果AC ? BD,BE ?CF ,且BE//CF,那么AE//DF .为
什么?
解:因为BE//CF(已知),
所以?EBC FCB?? ( ).
? ?
因为? ?? ?EBC EBA 180 ,? ?? ?FCB FCD 180 (平角的意义),
所以 ( ).
因为AC ? BD(已知),
所以AC?BCBDBC? ? (等式性质),
即 .
(完成以下说理过程)
26.已知:如图,△ABC是等边三角形,点D、E分别在边AB、BC的延长线上,且AD = BE,联结DC、
AE.
(1)试说明△BCD≌△ACE的理由; A
(2)如果BE = 2AB,求∠BAE的度数.
B E
C
D
(第26题图)
27.已知点A (0,4)、B(3,0),AB=5,建立直角坐标系并在直角坐标系中作出点A、B.若点C(与A、
B不重合)在坐标轴上,且AC=AB或BC=AB,求所有符合条件的点C的坐标.
4
青浦区2018学年第二学期七年级数学期末测试
参考答案与评分意见
一、填空题(每题2分,满分28分)
?2
? ?
1.?4; 2.-2; 3.>; 4.2; 5.20; 6.5 3; 7.50 ; 8.70 ; 9.? ??5,3 ;
?
10.10>c>6; 11.54 ; 12.△ABD与△ADC或△DCO与△ABO或△ABC与△DBC;
? ?
13.75°; 14.60 或120 ;
二、选择题(每题3分,满分共12分)
15.B; 16.A; 17.D; 18.C.
三、解答题(第19、20题各5分,第21、22题各6分,满分22分)
2
19.解:原式? ? ????5 25 5? …………………………………………………(1分)
?? ??
2
? ? 1
? ? ???5 25 …………………………………………………(1分)
?? ?? 5
2 1 1
? ? ? ? ………………………………………………( 分)
??5 25 1
5 5
? ?5 2…………………………………………………………………(2分)
【说明】没有过程,直接得结论扣2分.
4 3 5
20. 解:原式= 3 2 ?? 222 6……………………………………………………………………(3分)
4 3?? 5
=23 2 6…………………………………………………………………………(2分)
8
= 3 3
? 442 .……………………………………………………………………(1分)
21.(1)画图正确2分,标注字母正确1分,结论1分;
(2)画图正确1分,标注字母正确1分.
22.(1)? ??2,4 ,7;……………………………………………………………(1+1)分
(2)? ?5,3? ,等腰直角三角形;…………………………………………(1+1)分
(3)画图正确1分,标注字母正确1分.
四、解答题(第23、24题各7分,第25、26、27题各8分,满分38分)
1
23.解:根据题意:设?A 、?B 、?C的度数分别为3x、4x、5x.……(1分)
因为?A 、?B 、?C是△ABC的三个内角(已知),
? ?
所以??????A B C 180 (三角形的内角和等于180 ),……………(1分)
即 3xxx???45180.…………………………………………………(2分)
解得 x?15.……………………………………………………………(2分)
? ? ?
所以 ??A 45 ,??B 60 ,??C 75 .………………………………(1分)
24.解:(1) 因为ABAC? (已知),
所以△ABC是等腰三角形.
由ADBC? (已知),
1
得???1 BAC(等腰三角形的三线合一).……………………………(3分)
2
?
由? ?BAC 110 (已知),
1
? ?
得??? ?1 11055 .……………………………………………………(2分)
2
(2)因为△ABC是等腰三角形,ADBC? (已知),
所以BDCD? (等腰三角形的三线合一).……………………………(2分)
【说明】在用“等腰三角形的三线合一”性质时,前面两个条件有漏写的,要扣1分.
25.解: 两直线平行,内错角相等…………………………………………………(1分)
? ??EBA FCD…………………………………………………………(1分)
等角的补角相等……………………………………………………………(1分)
ABCD? .………………………………………………………………(1分)
在△ABE和△DCF中,
?ABCD? ,
?
?? ??ABE DCF, ……………………………………………………(1分)
??BECF? (已知),
所以△ABE≌△DCF(S.A.S),……………………………………(1分)
得???A D(全等三角形的对应角相等),…………………………(1分)
所以AEDF// (内错角相等,两直线平行).…………………………(1分)
26..解:(1)因为 △ABC是等边三角形,(已知)
所以 AB = BC = AC,
? ?? ??ABC ACB 60 .(等边三角形的三边相等,每一个内角等于60°)
所以 ∠DBC =∠ECA.(等角的补角相等)…………………………(1分)
2
因为 AD = BE,(已知)
所以 AD -AB = BE -BC.(等式性质)
即得 BD = CE.………………………………………………………(1分)
在△BCD和△ACE中,
?BCCA? ,
??? ??DBC ECA,
??BDCE? ,
所以 △BCD≌△ACE(S.A.S).…………………………………(2分)
(2)因为 BE = 2BC,(已知)
所以 BC = CE.
因为 AC = BC,(已证)
所以 AC = CE.(等量代换)
所以 ∠CAE =∠E.(等边对等角)…………………………………(2分)
因为 ∠ACB =∠CAE +∠E = 60°,(三角形的一个外角等于其不相邻的两个内角的和)
所以 ∠E = 30°.
因为 ∠ABE +∠E +∠BAE = 180°,(三角形三个内角的和等于180°)
所以 ∠BAE =180° -∠ABE -∠E = 90°.……………………………(2分)
27.解:正确画出坐标系…………(1分)
正确画出点A、B …………(1分)
以A为圆心,AB为半径画弧交坐标轴于点
C1 ? ,)03( C2 ,)90( C3 ,? )10( …………(3分)
以B为圆心,AB为半径画弧交坐标轴于点
C4 ? ,)02( C5 ,)08( C6 ,? )40( …………(3分)
3
同课章节目录
