人教版八年级数学下册18.1.1平行四边形的性质(第1课时)课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.1平行四边形的性质(第1课时)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 603.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
平行四边形的性质(第一课时)
情景引入
下面的图片中,有你熟悉的图形?
平行四边形的定义:
平行四边形.
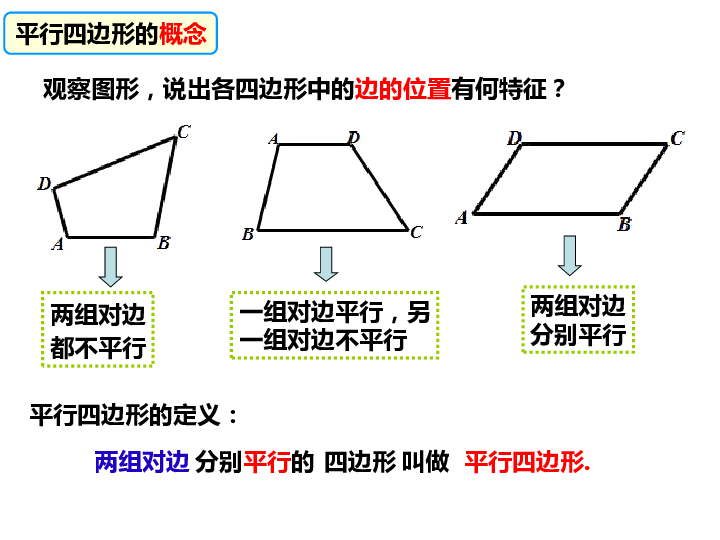
观察图形,说出各四边形中的边的位置有何特征?
两组对边
都不平行
一组对边平行,另
一组对边不平行
两组对边
分别平行
平行四边形的概念
两组对边
分别平行的
四边形
叫做
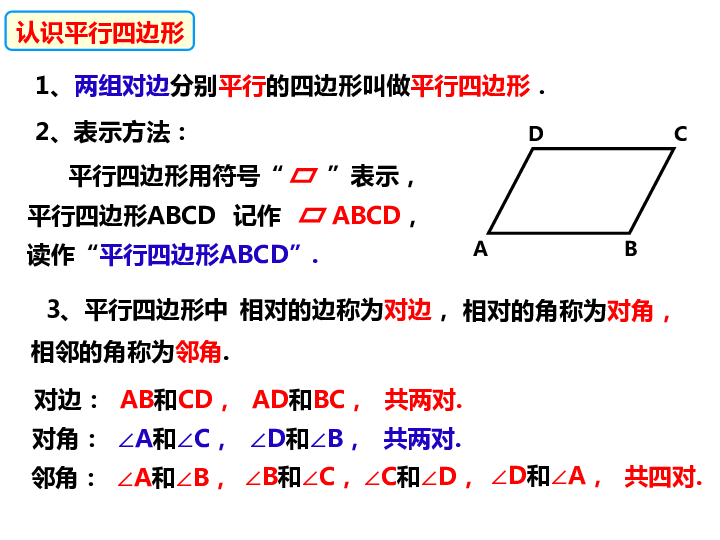
1、两组对边分别平行的四边形叫做平行四边形.
认识平行四边形
D
C
A
B
2、表示方法:
平行四边形用符号“
”表示,
平行四边形ABCD
记作
ABCD,
读作“平行四边形ABCD”.
3、平行四边形中
相邻的角称为邻角.
相对的角称为对角,
相对的边称为对边,
对边:
AB和CD,
共两对.
AD和BC,
对角:
∠A和∠C,
共两对.
∠D和∠B,
邻角:
∠A和∠B,
∠B和∠C,
∠C和∠D,
共四对.
∠D和∠A,
两组对边分别平行的四边形叫做平行四边形.
理解定义
D
C
A
B
几何语言
:
∵
AB∥
CD,
∴
四边形ABCD是平行四边形
反过来
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
注意:
AD∥
BC
AD∥
BC
AB∥
CD
AD∥
BC
又是它的一个性质.
平行四边形的定义
既是平行四边形的一种判定方法,
边、角还有什么性质呢?
AB∥
CD,
∠A+∠D
=180°
,
∠B+∠C=180°,
D
C
A
B
平行四边形的
相邻的内角
除此以外,
对边平行,
互为补角.
平行四边形中,
平行四边形的
对边平行
∠A+∠B=180°,
∠C+∠D
=180°
平行四边形的
邻角互补
AD∥
BC
边、角还有什么性质呢?
D
C
A
B
平行四边形的
相邻的内角
除此以外,
对边平行,
互为补角.
平行四边形中,
1、平行四边形的对边相等.
猜想:
2、平行四边形的对角相等.
D
C
A
B
证明:
∵
四边形ABCD是平行四边形
∴
AD∥
BC,AB
∥
CD
∴
∠A+∠B=180°
∠A+∠D=180°
∴
∠B=∠D
同理可得
∠A=∠C
有关四边形的问题
(ASA)
常常可转化为
已知:如图,四边形ABCD中,AB∥
DC,AD∥
BC.
求证:(1)
AB=DC,AD=BC;
连接AC
∵
AB∥
DC,AD∥
BC
∴
∠BAC=∠DCA,
验证猜想
D
C
A
B
证明
(1):
∠BCA=∠DAC
在△ABC和△CDA中
∴
△ABC
≌△CDA
∵
(公共边)
∠BCA=∠DAC
AC=CA
∠BAC=∠DCA
(2)
∠DAB=∠DCB,∠B=∠D.
∴
AB=DC,
AD=BC
(2)
∴
∠B=∠D
∠DCB
∵
∠DAB=
∠BAC+
∠DAC
=
∠DCA+
∠BCA
由(1)知:
△ABC≌△CDA
∴
∠DAB=∠DCA
方法技巧:
三角形的问题来处理.
D
C
A
B
由此得到平行四边形的下列性质:
性质1
性质2
平行四边形的对边相等.
平行四边形的对角相等.
D
C
A
B
平行四边形的性质
边的性质:
平行四边形的对边平行
平行四边形的对角相等,
归纳总结
角的性质:
几何语言
:
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
AD∥
BC
(平行四边形的对边平行)
AB=CD,
AD=BC
(平行四边形的对边相等)
∴
∠A=∠C,
∵
四边形ABCD是平行四边形
∠B=∠D
(平行四边形的对角相等)
(平行四边形的邻角互补)
且相等.
∠D+∠A
=180°
∠B+∠C=180°
∠A+∠B=180°,
∠C+∠D
=180°,
邻角互补.
几何语言
:
1、如图:在
ABCD中,根据已知你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
对应练习
方法技巧:
平行四边形中
知道其中两边
可求出另外三个角的度数,
知道一角
可求出另外两边的长度.
2、如图,在□
ABCD中.
(1)
若∠A=130°,则∠B=______
,∠C=______
,∠D=______.
(3)
若∠A+
∠C=
200°,则∠A=
,∠B=
.
(2)
若AB=3,BC=5,则它的周长=
______.
C
D
A
B
50°
130°
50°
对应练习
16
(4)
平行四边形ABCD的周长为40cm,两邻边AB,BC之比为2:3,则AB=
,BC=
.
12cm
100°
80°
8cm
2x
3x
平行四边形的邻边之和等于周长的一半
3、在
ABCD中,∠A
比∠B大60°,求这个平行四边形的四个内角的度数.
∴
AD∥
BC
∴
∠A
+∠
B=180°
又∵
∠A
-∠
B=60°
∴
∠A
=120°,
∠
B=60°
∴
∠A
=∠
C
=120°,
答:这个平行四边形的四个内角的度数分别是120°,
60°,120°,
60°.
C
D
A
B
∵
四边形ABCD是平行四边形
解:
∠
B=∠D
=60°
(平行四边形的对角相等)
对应练习
4、
已知:如图,
ABCD中,BE平分∠ABC交AD于点E.
(1)
如果AE=2,求CD的长;
(2)
如果∠AEB=40°,求
∠C
的度数.
∵
BE平分∠ABC
∴
∠ABE=∠EBC
A
B
C
D
E
解:(1)
(平行四边形的对边平行)
∵
四边形ABCD是平行四边形
∴
AD∥
BC
∴
∠AEB=∠EBC
(两直线平行内错角相等)
∴
∠ABE=∠AEB
∴
AB=AE=2
又∵
CD=AB
(平行四边形的对边相等)
∴
CD=2
对应练习
4、已知:如图,
ABCD中,BE平分∠ABC交AD于点E.
(1)
如果AE=2,求CD的长;
(2)
如果∠AEB=40°,求
∠C
的度数.
由(1)得∠ABE=∠AEB,
A
B
C
D
E
解:(2)
且∠AEB=40°
∴
∠ABE=∠AEB=40°
∴
∠A
=180°-(∠ABE+∠AEB)
=100°
又∵
∠C=∠A
(平行四边形的对角相等)
∴
∠C
=100°
对应练习
5、已知:如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△
.求证:△ABC的顶点分别是△
三边的中点.
证明:∵
AB∥
B'C,BC∥
AB'
同理:
同理:
∴△ABC的顶点分别是△
三边的中点.
∴
四边形ABCB'是平行四边形
D
C
A
B
平行四边形的性质
边的性质:
平行四边形的对边平行
平行四边形的对角相等,
角的性质:
几何语言
:
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
AD∥
BC
(平行四边形的对边平行)
AB=CD,
AD=BC
(平行四边形的对边相等)
∴
∠A=∠C,
∵
四边形ABCD是平行四边形
∠B=∠D
(平行四边形的对角相等)
(平行四边形的邻角互补)
且相等.
∠D+∠A
=180°
∠B+∠C=180°
∠A+∠B=180°,
∠C+∠D
=180°,
邻角互补.
几何语言
:
平行四边形的定义:
平行四边形.
两组对边
分别平行的
四边形
叫做
平行四边形的性质(第一课时)
情景引入
下面的图片中,有你熟悉的图形?
平行四边形的定义:
平行四边形.
观察图形,说出各四边形中的边的位置有何特征?
两组对边
都不平行
一组对边平行,另
一组对边不平行
两组对边
分别平行
平行四边形的概念
两组对边
分别平行的
四边形
叫做
1、两组对边分别平行的四边形叫做平行四边形.
认识平行四边形
D
C
A
B
2、表示方法:
平行四边形用符号“
”表示,
平行四边形ABCD
记作
ABCD,
读作“平行四边形ABCD”.
3、平行四边形中
相邻的角称为邻角.
相对的角称为对角,
相对的边称为对边,
对边:
AB和CD,
共两对.
AD和BC,
对角:
∠A和∠C,
共两对.
∠D和∠B,
邻角:
∠A和∠B,
∠B和∠C,
∠C和∠D,
共四对.
∠D和∠A,
两组对边分别平行的四边形叫做平行四边形.
理解定义
D
C
A
B
几何语言
:
∵
AB∥
CD,
∴
四边形ABCD是平行四边形
反过来
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
注意:
AD∥
BC
AD∥
BC
AB∥
CD
AD∥
BC
又是它的一个性质.
平行四边形的定义
既是平行四边形的一种判定方法,
边、角还有什么性质呢?
AB∥
CD,
∠A+∠D
=180°
,
∠B+∠C=180°,
D
C
A
B
平行四边形的
相邻的内角
除此以外,
对边平行,
互为补角.
平行四边形中,
平行四边形的
对边平行
∠A+∠B=180°,
∠C+∠D
=180°
平行四边形的
邻角互补
AD∥
BC
边、角还有什么性质呢?
D
C
A
B
平行四边形的
相邻的内角
除此以外,
对边平行,
互为补角.
平行四边形中,
1、平行四边形的对边相等.
猜想:
2、平行四边形的对角相等.
D
C
A
B
证明:
∵
四边形ABCD是平行四边形
∴
AD∥
BC,AB
∥
CD
∴
∠A+∠B=180°
∠A+∠D=180°
∴
∠B=∠D
同理可得
∠A=∠C
有关四边形的问题
(ASA)
常常可转化为
已知:如图,四边形ABCD中,AB∥
DC,AD∥
BC.
求证:(1)
AB=DC,AD=BC;
连接AC
∵
AB∥
DC,AD∥
BC
∴
∠BAC=∠DCA,
验证猜想
D
C
A
B
证明
(1):
∠BCA=∠DAC
在△ABC和△CDA中
∴
△ABC
≌△CDA
∵
(公共边)
∠BCA=∠DAC
AC=CA
∠BAC=∠DCA
(2)
∠DAB=∠DCB,∠B=∠D.
∴
AB=DC,
AD=BC
(2)
∴
∠B=∠D
∠DCB
∵
∠DAB=
∠BAC+
∠DAC
=
∠DCA+
∠BCA
由(1)知:
△ABC≌△CDA
∴
∠DAB=∠DCA
方法技巧:
三角形的问题来处理.
D
C
A
B
由此得到平行四边形的下列性质:
性质1
性质2
平行四边形的对边相等.
平行四边形的对角相等.
D
C
A
B
平行四边形的性质
边的性质:
平行四边形的对边平行
平行四边形的对角相等,
归纳总结
角的性质:
几何语言
:
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
AD∥
BC
(平行四边形的对边平行)
AB=CD,
AD=BC
(平行四边形的对边相等)
∴
∠A=∠C,
∵
四边形ABCD是平行四边形
∠B=∠D
(平行四边形的对角相等)
(平行四边形的邻角互补)
且相等.
∠D+∠A
=180°
∠B+∠C=180°
∠A+∠B=180°,
∠C+∠D
=180°,
邻角互补.
几何语言
:
1、如图:在
ABCD中,根据已知你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
对应练习
方法技巧:
平行四边形中
知道其中两边
可求出另外三个角的度数,
知道一角
可求出另外两边的长度.
2、如图,在□
ABCD中.
(1)
若∠A=130°,则∠B=______
,∠C=______
,∠D=______.
(3)
若∠A+
∠C=
200°,则∠A=
,∠B=
.
(2)
若AB=3,BC=5,则它的周长=
______.
C
D
A
B
50°
130°
50°
对应练习
16
(4)
平行四边形ABCD的周长为40cm,两邻边AB,BC之比为2:3,则AB=
,BC=
.
12cm
100°
80°
8cm
2x
3x
平行四边形的邻边之和等于周长的一半
3、在
ABCD中,∠A
比∠B大60°,求这个平行四边形的四个内角的度数.
∴
AD∥
BC
∴
∠A
+∠
B=180°
又∵
∠A
-∠
B=60°
∴
∠A
=120°,
∠
B=60°
∴
∠A
=∠
C
=120°,
答:这个平行四边形的四个内角的度数分别是120°,
60°,120°,
60°.
C
D
A
B
∵
四边形ABCD是平行四边形
解:
∠
B=∠D
=60°
(平行四边形的对角相等)
对应练习
4、
已知:如图,
ABCD中,BE平分∠ABC交AD于点E.
(1)
如果AE=2,求CD的长;
(2)
如果∠AEB=40°,求
∠C
的度数.
∵
BE平分∠ABC
∴
∠ABE=∠EBC
A
B
C
D
E
解:(1)
(平行四边形的对边平行)
∵
四边形ABCD是平行四边形
∴
AD∥
BC
∴
∠AEB=∠EBC
(两直线平行内错角相等)
∴
∠ABE=∠AEB
∴
AB=AE=2
又∵
CD=AB
(平行四边形的对边相等)
∴
CD=2
对应练习
4、已知:如图,
ABCD中,BE平分∠ABC交AD于点E.
(1)
如果AE=2,求CD的长;
(2)
如果∠AEB=40°,求
∠C
的度数.
由(1)得∠ABE=∠AEB,
A
B
C
D
E
解:(2)
且∠AEB=40°
∴
∠ABE=∠AEB=40°
∴
∠A
=180°-(∠ABE+∠AEB)
=100°
又∵
∠C=∠A
(平行四边形的对角相等)
∴
∠C
=100°
对应练习
5、已知:如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△
.求证:△ABC的顶点分别是△
三边的中点.
证明:∵
AB∥
B'C,BC∥
AB'
同理:
同理:
∴△ABC的顶点分别是△
三边的中点.
∴
四边形ABCB'是平行四边形
D
C
A
B
平行四边形的性质
边的性质:
平行四边形的对边平行
平行四边形的对角相等,
角的性质:
几何语言
:
∴
AB∥
CD,
∵
四边形ABCD是平行四边形
AD∥
BC
(平行四边形的对边平行)
AB=CD,
AD=BC
(平行四边形的对边相等)
∴
∠A=∠C,
∵
四边形ABCD是平行四边形
∠B=∠D
(平行四边形的对角相等)
(平行四边形的邻角互补)
且相等.
∠D+∠A
=180°
∠B+∠C=180°
∠A+∠B=180°,
∠C+∠D
=180°,
邻角互补.
几何语言
:
平行四边形的定义:
平行四边形.
两组对边
分别平行的
四边形
叫做
