12.2.2 全等三角形的判定SAS课时达标(含答案)
文档属性
| 名称 | 12.2.2 全等三角形的判定SAS课时达标(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 07:06:25 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
12.2.2全等三角形的判定SAS课时达标
一、选择题
1、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是(
)
A.SAS?
B.ASA?
C.SSS?
D.AAS
????????????
2、如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
A.65°?
B.95°?
C.45°?
D.100°
3、已知AC=DB,AO=DO,CD=100
m,则A,B两点间的距离(????
)
A.等于100
m?????
B.大于100
m
C.小于100
m?????
D.无法确定
4、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE.其中正确的有(????
)
A.1个???????????
B.2个????????
C.3个????????
D.4个
5、如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
6、如图,AD、BC相交于点O,OA=OD,OB=OC.下列结论正确的是(???
)
A.△AOB≌△DOC
?
B.△ABO≌△DOC???
C.∠A=∠C???
D.∠B=∠D
?
二、填空题
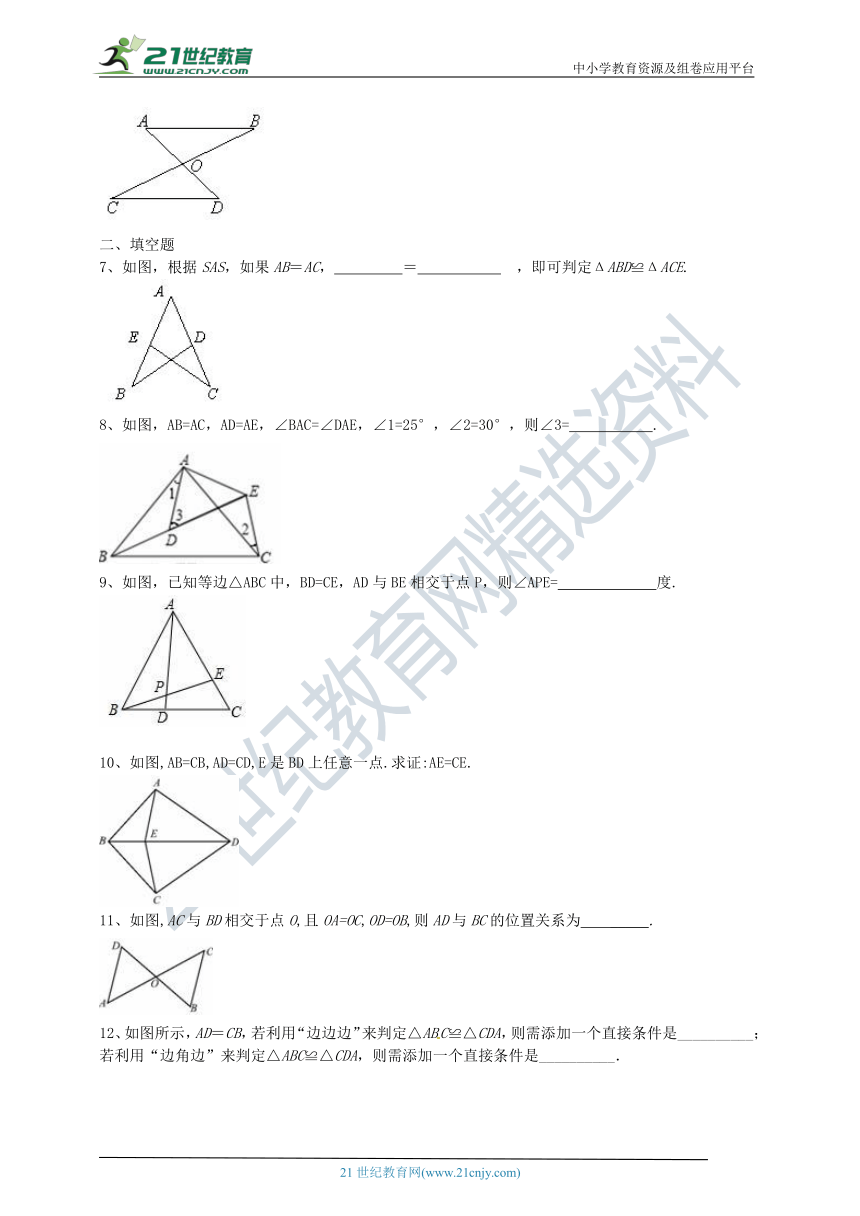
7、如图,根据SAS,如果AB=AC,????
=?????
?,即可判定ΔABD≌ΔACE.
?
8、如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=?????
.
9、如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE=??????
度.
10、如图,AB=CB,AD=CD,E是BD上任意一点.求证:AE=CE.
11、如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 _____.?
12、如图所示,AD=CB,若利用“边边边”来判定△ABC≌△CDA,则需添加一个直接条件是__________;若利用“边角边”来判定△ABC≌△CDA,则需添加一个直接条件是__________.
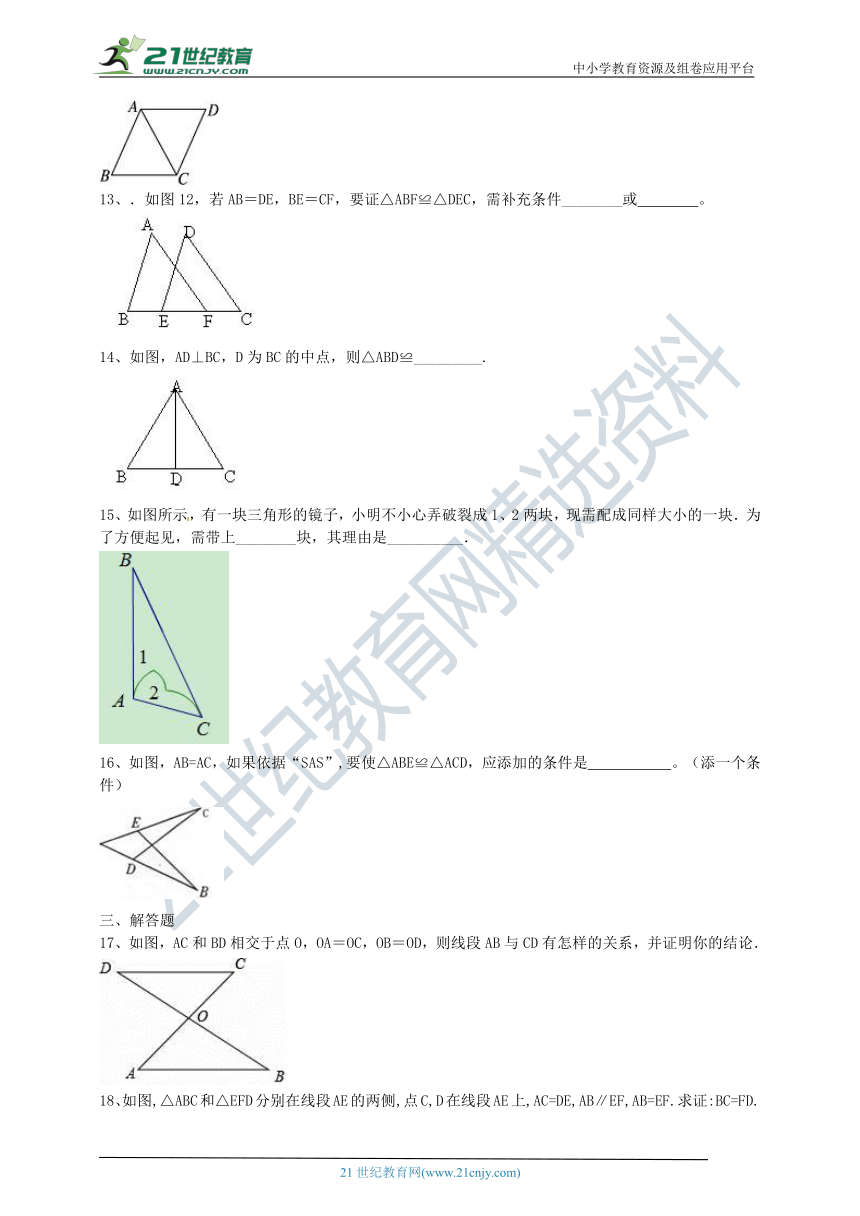
13、.如图12,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件________或 。
?
14、如图,AD⊥BC,D为BC的中点,则△ABD≌_________.
?
15、如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上________块,其理由是__________.
?
16、如图,AB=AC,如果依据“SAS”,要使△ABE≌△ACD,应添加的条件是?????
。(添一个条件)
三、解答题
17、如图,AC和BD相交于点O,OA=OC,OB=OD,则线段AB与CD有怎样的关系,并证明你的结论.
18、如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.
19、如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上,AB∥DE,且AB=DE,BE=CF.求证:△ABC≌△DEF.
20、已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE.求证:△AEC≌△BDC.
21、如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
22、如图所示,A,F,C,D四点同在一直线上,AF=CD,AB∥DE,且AB=DE.求证:
(1)△ABC≌△DEF;
(2)∠CBF=∠FEC.
参考答案
一、选择题
1、A
2、B
3、A
4、C
5、C
6、A?
二、填空题
7、AD=AE;
8、550??
解析:在△ABD与△ACE中,
∵
,∴
.
又∵
,,∴
.∴
.
∵
,,,∴
.
9、60??
解析:∵
△ABC是等边三角形,∴∠ABD=∠C,AB=AC.
∵
BD=CE,∴
△ABD≌△BCE,∴
∠BAD=∠CBE.
∵
,∴
,∴
.
10、证明:在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
∴∠ABE=∠CBE.
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
11、平行
12、AB=CD ∠CAD=∠ACB
13、∠B=∠DEC
AF=DC
14、?△ACD
15、1,有两边及其夹角对应相等的两个三角形全等??
16、AD=AE或EC=DB
三、解答题
17、【解析】AB=CD,AB∥CD,
在△AOB和△COD中,,
∴△AOB≌△COD(SAS
)
∴AB=CD,∠B=∠D
∴AB∥CD.
18、证明:∵AB∥EF,∴∠A=∠E.
在△ABC和△EFD中,
∴△ABC≌△EFD,∴BC=FD.
19、证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BE+EC=FC+EC,
即BC=EF.???????????
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
21、解:∵AB∥DC,
∴∠C=∠A,
∵AE=CF,
∴AE+EF=CF+EF,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS).
22、证明:(1)∵AB∥DE,
∴∠A=∠D.
又∵AF=CD,
∴AF+FC=CD+FC.
∴AC=DF.
∵AB=DE,
∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,
∴BC=EF,∠ACB=∠DFE.
∵FC=CF,
∴△FBC≌△CEF(SAS).
∴∠CBF=∠FEC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2.2全等三角形的判定SAS课时达标
一、选择题
1、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是(
)
A.SAS?
B.ASA?
C.SSS?
D.AAS
????????????
2、如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
A.65°?
B.95°?
C.45°?
D.100°
3、已知AC=DB,AO=DO,CD=100
m,则A,B两点间的距离(????
)
A.等于100
m?????
B.大于100
m
C.小于100
m?????
D.无法确定
4、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE.其中正确的有(????
)
A.1个???????????
B.2个????????
C.3个????????
D.4个
5、如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
6、如图,AD、BC相交于点O,OA=OD,OB=OC.下列结论正确的是(???
)
A.△AOB≌△DOC
?
B.△ABO≌△DOC???
C.∠A=∠C???
D.∠B=∠D
?
二、填空题
7、如图,根据SAS,如果AB=AC,????
=?????
?,即可判定ΔABD≌ΔACE.
?
8、如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=?????
.
9、如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE=??????
度.
10、如图,AB=CB,AD=CD,E是BD上任意一点.求证:AE=CE.
11、如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 _____.?
12、如图所示,AD=CB,若利用“边边边”来判定△ABC≌△CDA,则需添加一个直接条件是__________;若利用“边角边”来判定△ABC≌△CDA,则需添加一个直接条件是__________.
13、.如图12,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件________或 。
?
14、如图,AD⊥BC,D为BC的中点,则△ABD≌_________.
?
15、如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上________块,其理由是__________.
?
16、如图,AB=AC,如果依据“SAS”,要使△ABE≌△ACD,应添加的条件是?????
。(添一个条件)
三、解答题
17、如图,AC和BD相交于点O,OA=OC,OB=OD,则线段AB与CD有怎样的关系,并证明你的结论.
18、如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.
19、如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上,AB∥DE,且AB=DE,BE=CF.求证:△ABC≌△DEF.
20、已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE.求证:△AEC≌△BDC.
21、如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
22、如图所示,A,F,C,D四点同在一直线上,AF=CD,AB∥DE,且AB=DE.求证:
(1)△ABC≌△DEF;
(2)∠CBF=∠FEC.
参考答案
一、选择题
1、A
2、B
3、A
4、C
5、C
6、A?
二、填空题
7、AD=AE;
8、550??
解析:在△ABD与△ACE中,
∵
,∴
.
又∵
,,∴
.∴
.
∵
,,,∴
.
9、60??
解析:∵
△ABC是等边三角形,∴∠ABD=∠C,AB=AC.
∵
BD=CE,∴
△ABD≌△BCE,∴
∠BAD=∠CBE.
∵
,∴
,∴
.
10、证明:在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
∴∠ABE=∠CBE.
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
11、平行
12、AB=CD ∠CAD=∠ACB
13、∠B=∠DEC
AF=DC
14、?△ACD
15、1,有两边及其夹角对应相等的两个三角形全等??
16、AD=AE或EC=DB
三、解答题
17、【解析】AB=CD,AB∥CD,
在△AOB和△COD中,,
∴△AOB≌△COD(SAS
)
∴AB=CD,∠B=∠D
∴AB∥CD.
18、证明:∵AB∥EF,∴∠A=∠E.
在△ABC和△EFD中,
∴△ABC≌△EFD,∴BC=FD.
19、证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BE+EC=FC+EC,
即BC=EF.???????????
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
21、解:∵AB∥DC,
∴∠C=∠A,
∵AE=CF,
∴AE+EF=CF+EF,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS).
22、证明:(1)∵AB∥DE,
∴∠A=∠D.
又∵AF=CD,
∴AF+FC=CD+FC.
∴AC=DF.
∵AB=DE,
∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,
∴BC=EF,∠ACB=∠DFE.
∵FC=CF,
∴△FBC≌△CEF(SAS).
∴∠CBF=∠FEC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
