沪教版(上海)九年级第一学期数学 24.5 相似三角形性质 课件 (共15张PPT)
文档属性
| 名称 | 沪教版(上海)九年级第一学期数学 24.5 相似三角形性质 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 08:17:42 | ||
图片预览


文档简介
(共15张PPT)
24.5
相似三角形性质
复习回顾
1、相似三角形的判断有哪些?
2、相似三角形已学过哪些性质?
3、三角形中的主要线段有哪些?全等三角形中这些线段有何关系?
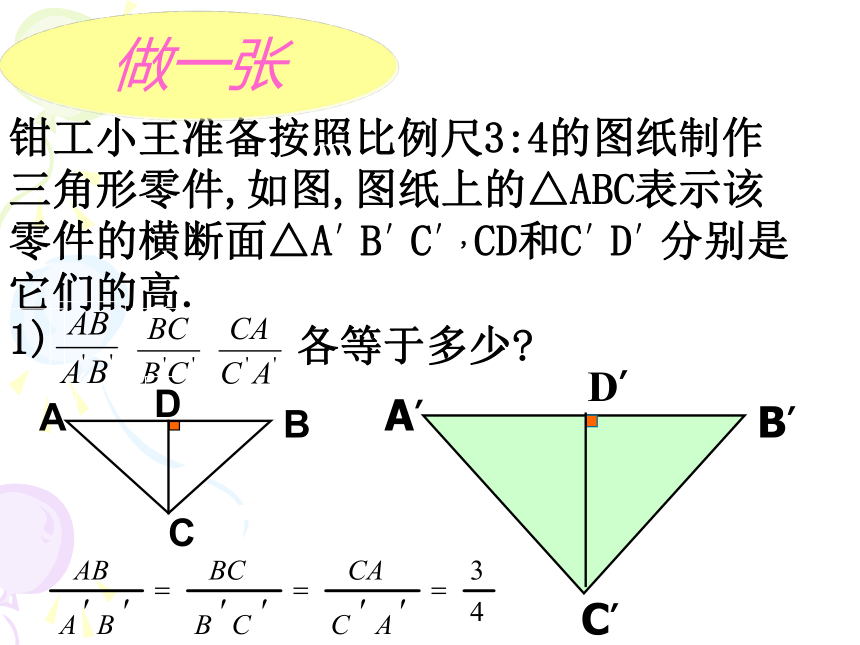
钳工小王准备按照比例尺3:4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.
做一张
1)
各等于多少?
C
A
B
D
C′
A′
B′
D′
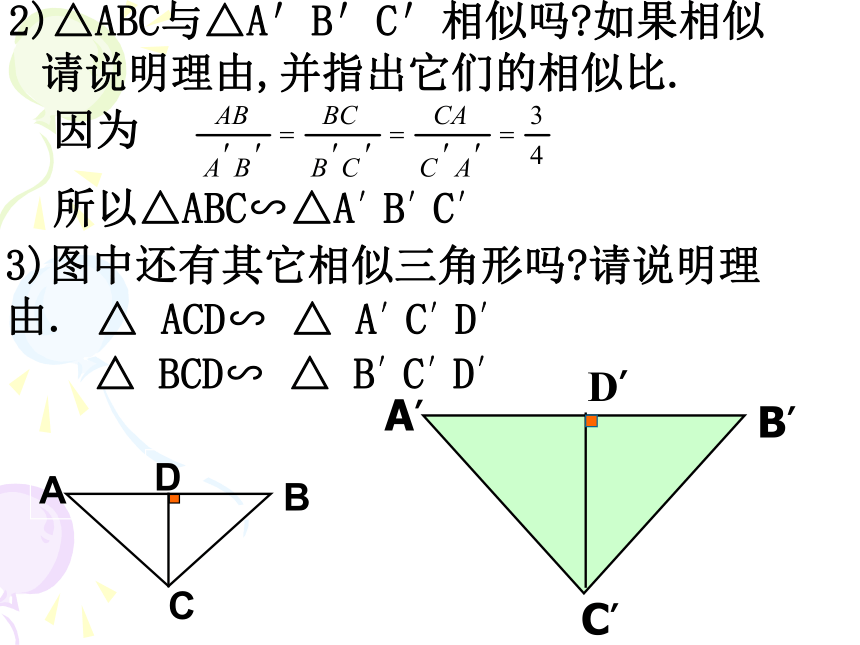
2)△ABC与△A′B′C′相似吗?如果相似请说明理由,并指出它们的相似比.
C
A
B
D
D′
B′
A′
C′
因为
所以△ABC∽△A′B′C′
△
ACD∽
△
A′C′D′
△
BCD∽
△
B′C′D′
3)图中还有其它相似三角形吗?请说明理由.
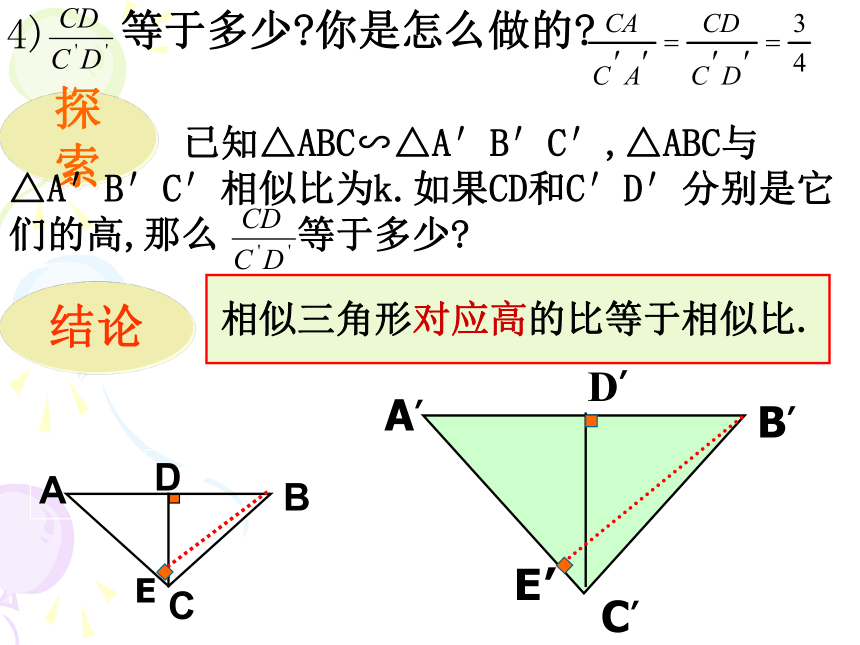
4)
等于多少?你是怎么做的?
C
A
B
D
D′
B′
A′
C′
探索
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.如果CD和C′D′分别是它们的高,那么
等于多少?
结论
相似三角形对应高的比等于相似比.
E’
E
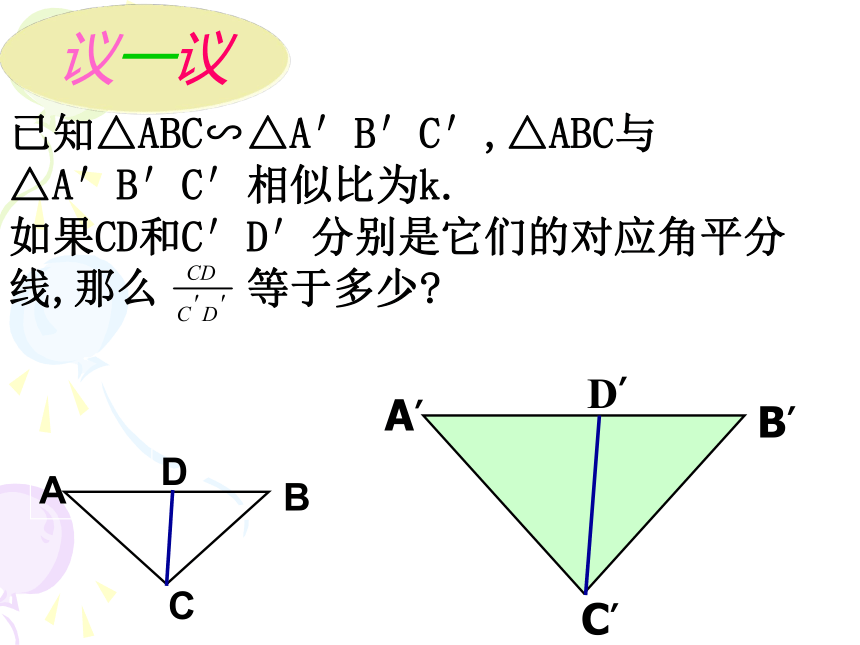
议一议
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.
如果CD和C′D′分别是它们的对应角平分线,那么
等于多少?
C
A
B
D
D′
B′
A′
C′
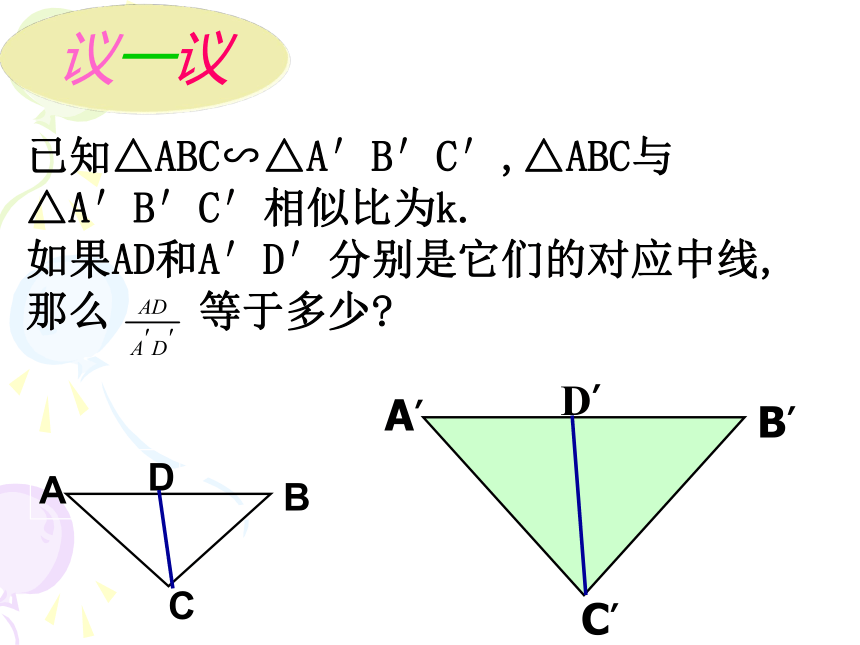
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.
如果AD和A′D′分别是它们的对应中线,那么
等于多少?
议一议
C
A
B
D
A′
D′
B′
C′
定理1:相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。
相似三角形的性质
1.如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是_____,对应边上的中线的比是______
。
2.△ABC与△A'B'C'的相似比为3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_____
。
2:3
2:3
16cm
4.如图△ABC∽△A’B′C′,对应中线AD=6cm,A’D’=10cm,若BC=12cm,则B’C′=______
。
20cm
3、已知△ABC∽△A′B′C′,如果AD和A′D′分别是它们的对应角平分线,
AD=8cm,A’D’=3cm,则△ABC与△A′B′C′对应高的比
8:3
如图所示,△ABC中,底边BC=80cm,高
AD=60cm,四边形PQRS是长方形.
(1)△ASR与△ABC相似吗?为什么?
(2)当矩形边PQ与PS之比为2比1,求长方形PQRS的边长.
解:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是长方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设长方形PQRS的边PS为xcm,
则AE=(60-x)cm,SR=PQ=2x
解得,X=24.2X=48
所以长方形PQRS的边长分别为24cm,48cm.
A
B
C
S
R
E
P
D
Q
(相似三角形对应高的比等于相似比)
例
题
解
析
x
,60-x
如图所示,在等腰△ABC中,底边BC=60cm,高
AD=40cm,四边形PQRS是正方形.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
解:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的边长为24cm.
A
B
C
S
R
E
P
D
Q
(相似三角形对应高的比等于相似比)
例
题
巩固
x
40-x
巩
固
练
习
如图所示,在矩形DEFG内接于△ABC,点D、E在BC上,点F,G分别在AC,AB上,且DE=2EF,BC=21mm,
△ABC的高AH=14mm,求矩形DEFG的面积。
A
B
C
D
E
H
G
F
A
相似三角形的性质
(特别注意“对应”二字)
对应角相等
对应边成比例
对应高的比、对应中线的比、对应角平分线的比都等于相似比.
E
?
A
B
C
D
F
?
E'
A′
B′
C′
D′
F'
结束寄语
培养回顾联想已学知识,探索学习后续知识的能力,可使每个有自信心的人到达希望的顶峰.
下
课!
24.5
相似三角形性质
复习回顾
1、相似三角形的判断有哪些?
2、相似三角形已学过哪些性质?
3、三角形中的主要线段有哪些?全等三角形中这些线段有何关系?
钳工小王准备按照比例尺3:4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.
做一张
1)
各等于多少?
C
A
B
D
C′
A′
B′
D′
2)△ABC与△A′B′C′相似吗?如果相似请说明理由,并指出它们的相似比.
C
A
B
D
D′
B′
A′
C′
因为
所以△ABC∽△A′B′C′
△
ACD∽
△
A′C′D′
△
BCD∽
△
B′C′D′
3)图中还有其它相似三角形吗?请说明理由.
4)
等于多少?你是怎么做的?
C
A
B
D
D′
B′
A′
C′
探索
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.如果CD和C′D′分别是它们的高,那么
等于多少?
结论
相似三角形对应高的比等于相似比.
E’
E
议一议
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.
如果CD和C′D′分别是它们的对应角平分线,那么
等于多少?
C
A
B
D
D′
B′
A′
C′
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.
如果AD和A′D′分别是它们的对应中线,那么
等于多少?
议一议
C
A
B
D
A′
D′
B′
C′
定理1:相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。
相似三角形的性质
1.如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是_____,对应边上的中线的比是______
。
2.△ABC与△A'B'C'的相似比为3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_____
。
2:3
2:3
16cm
4.如图△ABC∽△A’B′C′,对应中线AD=6cm,A’D’=10cm,若BC=12cm,则B’C′=______
。
20cm
3、已知△ABC∽△A′B′C′,如果AD和A′D′分别是它们的对应角平分线,
AD=8cm,A’D’=3cm,则△ABC与△A′B′C′对应高的比
8:3
如图所示,△ABC中,底边BC=80cm,高
AD=60cm,四边形PQRS是长方形.
(1)△ASR与△ABC相似吗?为什么?
(2)当矩形边PQ与PS之比为2比1,求长方形PQRS的边长.
解:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是长方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设长方形PQRS的边PS为xcm,
则AE=(60-x)cm,SR=PQ=2x
解得,X=24.2X=48
所以长方形PQRS的边长分别为24cm,48cm.
A
B
C
S
R
E
P
D
Q
(相似三角形对应高的比等于相似比)
例
题
解
析
x
,60-x
如图所示,在等腰△ABC中,底边BC=60cm,高
AD=40cm,四边形PQRS是正方形.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
解:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的边长为24cm.
A
B
C
S
R
E
P
D
Q
(相似三角形对应高的比等于相似比)
例
题
巩固
x
40-x
巩
固
练
习
如图所示,在矩形DEFG内接于△ABC,点D、E在BC上,点F,G分别在AC,AB上,且DE=2EF,BC=21mm,
△ABC的高AH=14mm,求矩形DEFG的面积。
A
B
C
D
E
H
G
F
A
相似三角形的性质
(特别注意“对应”二字)
对应角相等
对应边成比例
对应高的比、对应中线的比、对应角平分线的比都等于相似比.
E
?
A
B
C
D
F
?
E'
A′
B′
C′
D′
F'
结束寄语
培养回顾联想已学知识,探索学习后续知识的能力,可使每个有自信心的人到达希望的顶峰.
下
课!
