上海市龙柏高中2019-2020学年高中物理沪科版选修3-4:光的波动性 单元测试题(含解析)
文档属性
| 名称 | 上海市龙柏高中2019-2020学年高中物理沪科版选修3-4:光的波动性 单元测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 640.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-23 05:26:04 | ||
图片预览


文档简介
光的波动性
1.用波长为的平行单色光照射双缝,在光屏上偏离中心的P点处恰好出现亮条纹,则( )
A.改用波长为2的单色光照射,P点处一定出现亮条纹
B.改用波长为的单色光照射,P点处—定出现亮条纹
C.改用波长为2的单色光照射,P点处一定出现暗条纹
D.改用波长为的单色光照射,P点处一定出现暗条纹
2.一束单色光从空气射向某种介质的表面,光路如图所示。则该介质的折射率为( )
A.2.00 B.0.50 C.0.58 D.1.73
3.在一次观察光的衍射实验中,观察到如图所示的清晰的亮暗相间的图样,那么障碍物是下列给出的( )
A.很小的不透明圆板
B.很大的中间有大圆孔的不透明挡板
C.很大的不透明圆板
D.很大的中间有小圆孔的不透明挡板
4.下列有关光学现象的说法正确的是( )
A.光从光密介质射入光疏介质,其频率不变,传播速度变小
B.光从光密介质射入光疏介质,若入射角大于临界角,则一定发生全反射
C.光的干涉、衍射现象证明了光具有波动性
D.做双缝干涉实验时,用红光替代紫光,相邻明条纹间距变小
5.下列说法正确的是( )
A.观测到某星球上A元素发出的光的频率大于地球上A元素发出的光的频率,则该星球正在靠近地球
B.自然光包含着垂直于传播方向上的沿一切方向振动的光,且沿各个方向振动的光的强度均相同
C.在岸边观察水中的鱼,鱼的实际深度比看到的要浅一些
D.在光的双缝干涉实验中,若仅将入射光由绿光改为红光,则干涉条纹间距变宽
E.若红光由真空进入折射率为n的介质中,则红光在介质中的波长与其在真空中的波长的比值为n
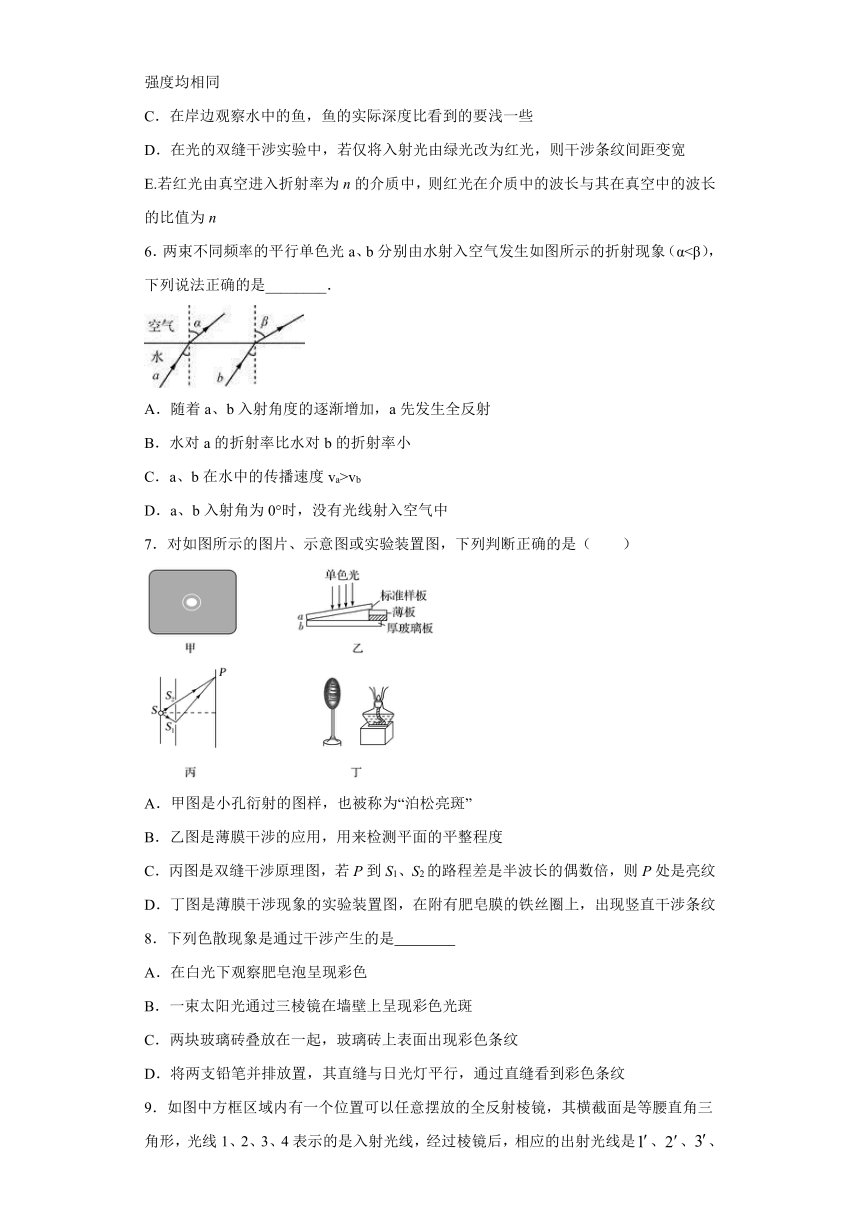
6.两束不同频率的平行单色光a、b分别由水射入空气发生如图所示的折射现象(α<β),下列说法正确的是________.
A.随着a、b入射角度的逐渐增加,a先发生全反射
B.水对a的折射率比水对b的折射率小
C.a、b在水中的传播速度va>vb
D.a、b入射角为0°时,没有光线射入空气中
7.对如图所示的图片、示意图或实验装置图,下列判断正确的是( )
A.甲图是小孔衍射的图样,也被称为“泊松亮斑”
B.乙图是薄膜干涉的应用,用来检测平面的平整程度
C.丙图是双缝干涉原理图,若P到S1、S2的路程差是半波长的偶数倍,则P处是亮纹
D.丁图是薄膜干涉现象的实验装置图,在附有肥皂膜的铁丝圈上,出现竖直干涉条纹
8.下列色散现象是通过干涉产生的是
A.在白光下观察肥皂泡呈现彩色
B.一束太阳光通过三棱镜在墙壁上呈现彩色光斑
C.两块玻璃砖叠放在一起,玻璃砖上表面出现彩色条纹
D.将两支铅笔并排放置,其直缝与日光灯平行,通过直缝看到彩色条纹
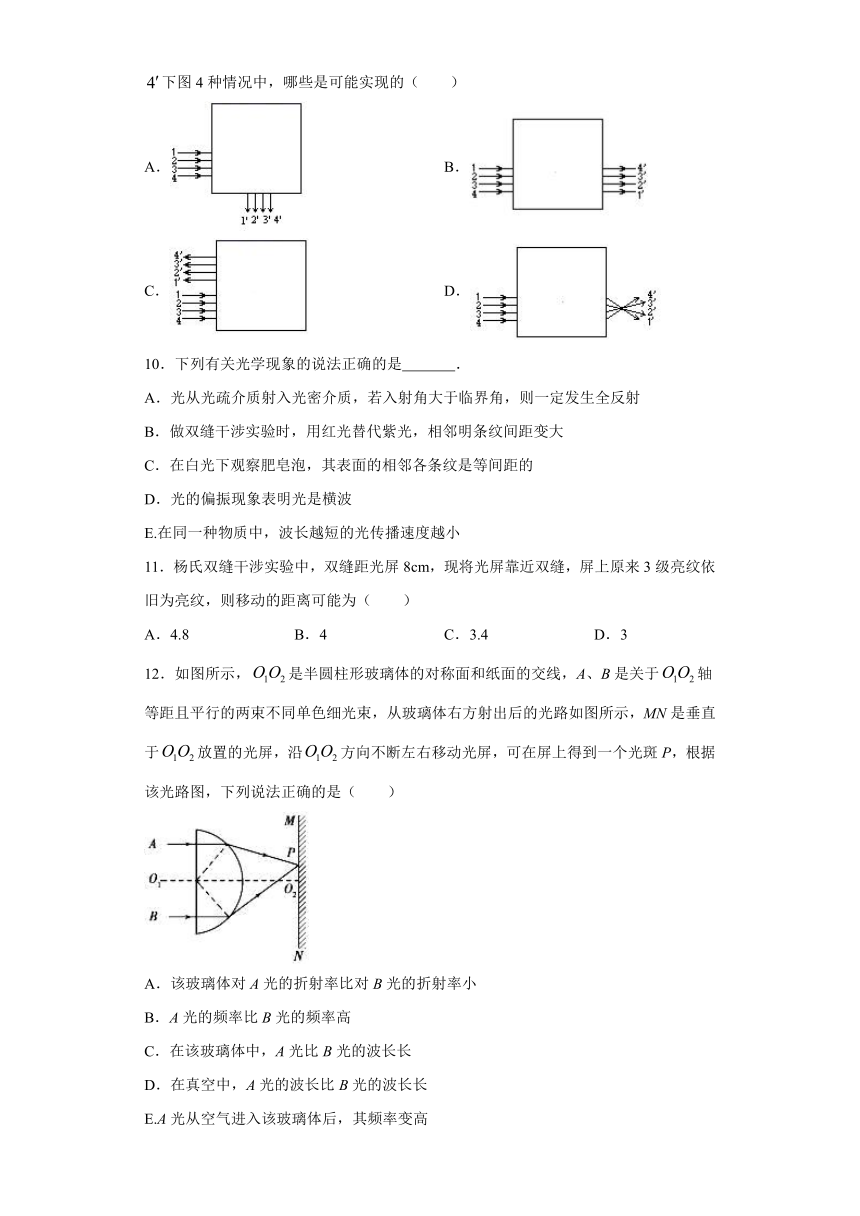
9.如图中方框区域内有一个位置可以任意摆放的全反射棱镜,其横截面是等腰直角三角形,光线1、2、3、4表示的是入射光线,经过棱镜后,相应的出射光线是、、、下图4种情况中,哪些是可能实现的( )
A. B.
C. D.
10.下列有关光学现象的说法正确的是 .
A.光从光疏介质射入光密介质,若入射角大于临界角,则一定发生全反射
B.做双缝干涉实验时,用红光替代紫光,相邻明条纹间距变大
C.在白光下观察肥皂泡,其表面的相邻各条纹是等间距的
D.光的偏振现象表明光是横波
E.在同一种物质中,波长越短的光传播速度越小
11.杨氏双缝干涉实验中,双缝距光屏8cm,现将光屏靠近双缝,屏上原来3级亮纹依旧为亮纹,则移动的距离可能为( )
A.4.8 B.4 C.3.4 D.3
12.如图所示,是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于放置的光屏,沿方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
A.该玻璃体对A光的折射率比对B光的折射率小
B.A光的频率比B光的频率高
C.在该玻璃体中,A光比B光的波长长
D.在真空中,A光的波长比B光的波长长
E.A光从空气进入该玻璃体后,其频率变高
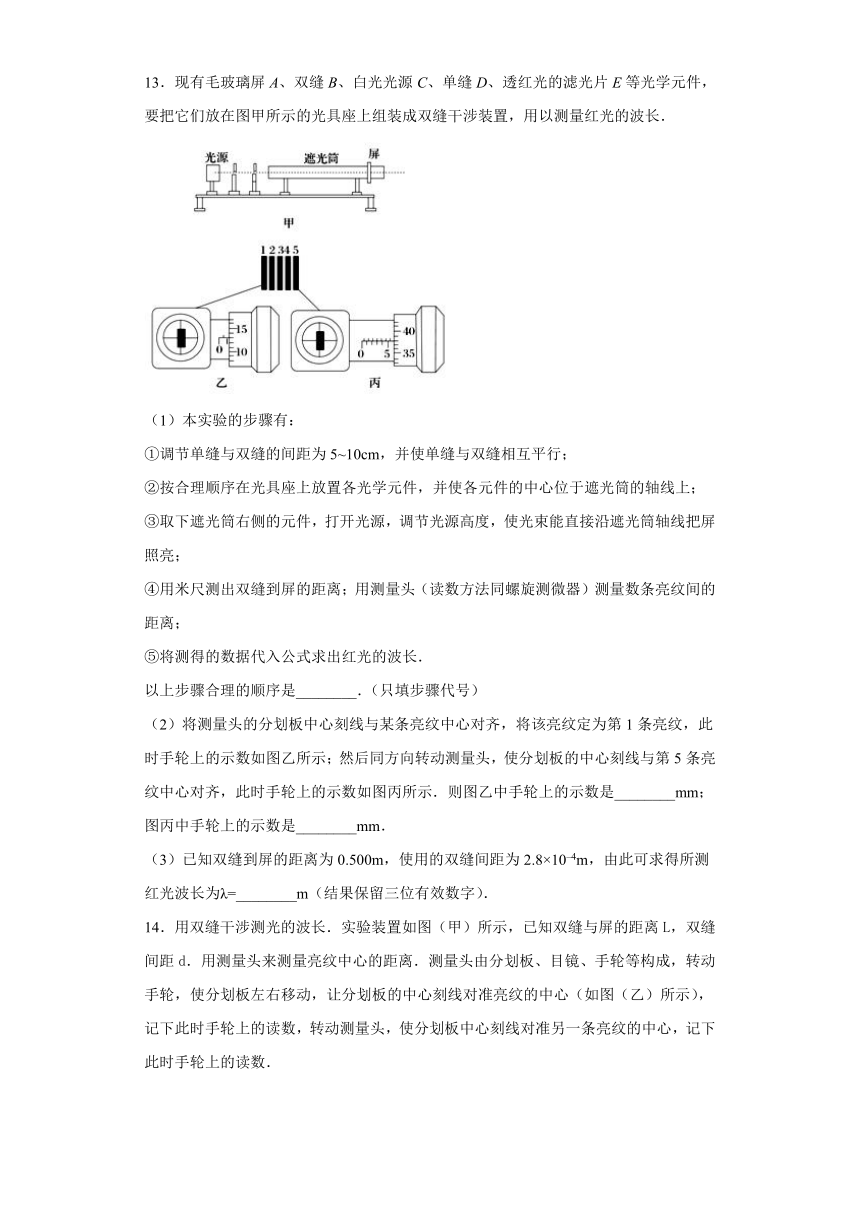
13.现有毛玻璃屏A、双缝B、白光光源C、单缝D、透红光的滤光片E等光学元件,要把它们放在图甲所示的光具座上组装成双缝干涉装置,用以测量红光的波长.
(1)本实验的步骤有:
①调节单缝与双缝的间距为5~10cm,并使单缝与双缝相互平行;
②按合理顺序在光具座上放置各光学元件,并使各元件的中心位于遮光筒的轴线上;
③取下遮光筒右侧的元件,打开光源,调节光源高度,使光束能直接沿遮光筒轴线把屏照亮;
④用米尺测出双缝到屏的距离;用测量头(读数方法同螺旋测微器)测量数条亮纹间的距离;
⑤将测得的数据代入公式求出红光的波长.
以上步骤合理的顺序是________.(只填步骤代号)
(2)将测量头的分划板中心刻线与某条亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图乙所示;然后同方向转动测量头,使分划板的中心刻线与第5条亮纹中心对齐,此时手轮上的示数如图丙所示.则图乙中手轮上的示数是________mm;图丙中手轮上的示数是________mm.
(3)已知双缝到屏的距离为0.500m,使用的双缝间距为2.8×10–4m,由此可求得所测红光波长为λ=________m(结果保留三位有效数字).
14.用双缝干涉测光的波长.实验装置如图(甲)所示,已知双缝与屏的距离L,双缝间距d.用测量头来测量亮纹中心的距离.测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心(如图(乙)所示),记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数.
(1)首先调节________和滤光片的中心位于遮光筒的中心轴线上,并使_________和________竖直且互相平行.
(2)分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如图(丙)所示,则对准第1条时读数x1=__________mm(允许误差)、对准第4条时读数x2=_______________mm(允许误差)
(3)写出计算波长λ的表达式,λ=______(用x1、 x2 、L 、d表示,不用计算).
15.有一玻璃球冠,右侧面镀银,光源S位于其对称轴上,如图所示.从光源S发出的一细光束射到球面上的A点,其反射光恰好垂直于球冠的对称轴,折射进入玻璃球冠内的光经右侧镀银面第一次反射后恰能沿原路返回.若球面半径为R,球冠高为,玻璃折射率为,光在真空中的传播速度为c.求:
(1)光源S与球冠顶点M之间的距离SM;
(2)光在玻璃中的传播时间.
16.一半圆柱形透明物体横截面如图所示,底面镀银,表示平圆截面的圆心,一束光线在横截面内从点入射,经过面反射后从点射出。已知光线在点的入射角为,,,求:
①光线在点的折射角;
②透明物体的折射率。
17.如图所示,直角三角形ABC为某种透明介质的横截面,∠B=30°,BC=30cm,AB面涂有反光材料.某单色光从BC上的D点垂直BC射入介质,经AB面反射后从AC面上射出,射出方向与AB面垂直.已知BD=21cm,不考虑光在AC面的反射.求:
(i)介质的折射率;
(ii)光在介质中的传播时间.
18.一半径为R的玻璃板球,O点是半球的球心,虚线OO?表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为,现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线,已知),求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
参考答案
1.B
【解析】
出现亮条纹是因为光程差为波长的整数倍,为n,如果n为奇数,当改用波长为2的单色光照射,P点的光程差为此时半波长的奇数倍,为暗条纹,因此AC错误,如果换成的单色光,则光程差一定为整数倍,则一定是亮条纹,B正确D错误
2.D
【解析】
由题单色光从空气射向该介质时,入射角,折射角,则该介质的折射率为
故D正确,ABC错误。
故选D。
3.D
【解析】
很大的中间有大圆孔的不透明挡板和很大的不透明圆板不会发生衍射现象,很小的不透明圆板出现泊松亮斑.
【详解】
A.用光照射很小的不透明圆板时后面出现一亮点,即泊松亮斑,故A错误;
B.很大的中间有大圆孔的不透明挡板时后面是一亮洞,不会出现衍射现象,故B错误;
C.很大的不透明圆板时后面是一片阴影,不会出现衍射现象,故C错误;
D.用光照射很大的中间有小圆孔的不透明挡板时是明暗相间的衍射图样,即发生衍射现象,故D正确.
【点睛】
该题考查单孔衍射的图样,要牢记单孔衍射和单缝衍射图样与障碍物或孔的尺寸是有关系的,不同的障碍物或孔出现的衍射图样是不一样的.
4.BC
【解析】
A.光从光密介质射入光疏介质,其频率不变,传播速度变大,选项A错误;
B.光从光密介质射入光疏介质,若入射角大于临界角,则一定发生全反射,选项B正确;
C.光的干涉、衍射现象证明了光具有波动性,选项C正确;
D.红光的波长大于紫光,做双缝干涉实验时,用红光替代紫光,根据可知,相邻明条纹间距变大,选项D错误。
故选BC。
5.ABD
【解析】
A.根据多普勒效应可以计算出物体相对运动的速度,所以通过测量星球上某些元素发出光波的频率,然后与地球上这些元素静止时发光的频率对照,就可以算出星球靠近或远离我们的速度,故A与题意相符;
B.自然光包含着垂直于传播方向上的沿一切方向振动的光,且沿各个方向振动的光的强度均相同,故B与题意相符;
C.在岸边观察水中的鱼,看到的鱼是由于鱼发出的光线经过水面折射形成的虚像,根据折射定律知折射角大于入射角,所以看到的鱼比实际深度要浅一些,故C与题意不符;
D.根据双缝干涉的宽度公式:可知,在光的双缝干涉实验中,若仅将入射光由绿光改为红光,波长变长,则干涉条纹间距变宽,故D与题意相符;
E.红光由真空进入折射率为n的介质中,频率不变,则
得红光在介质中的波长与其在真空中的波长的比值
故E与题意不符。
6.BC
【解析】
A.由图知,α<β,所以随着a、b入射角度的逐渐增加,折射角均增大,b光的折射角先达到90°,即b光先发生全反射,故A错误.
B.由于α<β,由折射定律知,折射率na小于nb,故B正确.
C.由v=c/n知,在水中的传播速度关系为va>vb,故C正确.
D.当a、b入射角为0°时,光线不偏折进入空气中.故D错误.
故选BC.
7.BC
【解析】
A.甲图是小孔衍射的图样,而“泊松亮斑”是圆板衍射,故不是“泊松亮斑”,故A错误;
B.乙图是薄膜干涉的应用,用来检测平面的平整程度。若干涉条纹是直的干涉条纹则表明平面平整,故B正确;
C.图是双缝干涉原理图,若P到S1、S2的路程差是光的半波长的偶数倍,则P是亮纹,若P到S1、S2的路程差是光的半波长的奇数倍,则P是暗纹,故C正确;
D.丁图是薄膜干涉现象的实验装置图,在附有肥皂膜的铁丝圈上,出现水平干涉条纹,故D错误。
故选BC。
8.AC
【解析】
A.肥皂泡在阳光下呈现彩色条纹是肥皂膜内外反射的光线,相互叠加产生的现象,这是光的干涉造成的,故A正确;
B.一束太阳光通过三棱镜在墙壁上呈现彩色光斑属于光的色散,B错误;
C.两块玻璃砖叠放在一起,玻璃砖上表面出现彩色条纹,时相互叠加产生的现象,这是光的干涉造成的,C正确;
D.两支铅笔并排放置,其直缝与日光灯平行,通过直缝看到彩色条纹,这是光的衍射现象,D错误.
故选AC。
9.ABC
【解析】
A.将全反射棱镜如图放置,可满足要求,选项A正确;
B. 将全反射棱镜如图放置,可满足要求,选项B正确;
C. 将全反射棱镜如图放置,可满足要求,选项C正确;
D. 全反射棱镜对光路有两种控制作用:将光的传播方向改变90°,或是改变180°,而没有会聚光线的作用,选项D选项错误。
10.BDE
【解析】
【详解】
A.全反射发生的条件是光从光密介质进入光疏介质,且入射角大于或等于临界角时,故A错误;
B.根据双缝干涉实验,相邻条纹间距,波长越长则干涉条纹间距越大,而红光的波长大于紫光波长,则红光的干涉条纹间距比紫光的大,故B正确;
C.根据以及不同颜色的光波长不同可知,不同颜色的光缠身的干涉条纹间距不同,故在白光下观察肥皂泡,其表面的相邻各条纹的间距是不等的,故C错误;
D.光的偏振现象证明了光是横波,纵波不能发生光的偏振现象,故D正确;
E.在同一种物质中,不同波长的光传播速度不同,波长越短,波速越小,故E正确.
11.ABCD
【解析】
【详解】
杨氏双缝干涉亮条纹的位置为
,k=0,±1,±2……
其中,d为双缝间距,D为双缝到光屏的距离,λ为光的波长。依题意有
,D其中,k为正整数,所以
,k=4,5,6,……
带入D0=8cm可得D =6 cm,4.8 cm,4 cm,3.4 cm,3 cm……故ABCD均正确。
故选ABCD。
12.ACD
【解析】
【详解】
ABD.光线通过玻璃体后,A光的偏折程度比B光的小,则该玻璃体对A光的折射率比对B光的折射率小,而折射率越大,光的频率越高,说明A光的频率比B光的频率低,由c=λγ知,在真空中,A光的波长比B光的长,故A、D正确,B错误;
C.设同一光线在真空中的波长为λ0,在玻璃体中的波长为λ,折射率为n,则
,
得:
在真空中,A光的波长比B光的波长长,而玻璃体对A光的折射率比对B光的折射率小,由λ=λ0/n知,在该玻璃体中,A光比B光的波长长.故C正确;
E. 光的频率由光源决定,与介质无关,则A光从空气进入该玻璃体后,其频率不变.故E错误.
13.③②①④⑤ 1.130 5.580 6.23×10–7
【解析】
【分析】
【详解】
(1)[1]为获取单色线光源,白色光源后面要有滤光片、单缝、双缝.所以各光学元件的字母排列顺序应为③ ② ① ④ ⑤.
(2) [2][3]螺旋测微器乙的固定刻度读数为1mm,可动刻度读数为0.01×13.0mm=0.130mm,则最终读数为1.130mm.螺旋测微器丙的固定刻度读数为5.5mm,可动刻度读数为0.01×38.0mm=0.380mm,则最终读数为5.580mm.相邻条纹的间距
.
(3)[4]根据得
14.(1)光源 单缝 双缝 (2)2.190 7.869 (3)d(x2 –x1 )/3L
【解析】
(1)首先调节光源和滤光片的中心位于遮光筒的中心轴线上,并使单缝和双缝竖直且互相平行.
(2)图丙中固定刻度读数为2mm,可动刻度读数为0.01×19.0=0.190mm,所以最终读数为2.190mm.
对准第4条亮纹时固定刻度读数为7.5mm,可动读数为0.01×36.9=0.369mm,所以最终读数为7.869mm.
(3)根据得:
点睛:解决本题的关键掌握螺旋测微器的读数方法,固定刻度读数加上可动刻度读数,不需估读.以及掌握条纹间距公式.
15.(1),(2)
【解析】
【分析】
考查折射定律,光的传播。
【详解】
(1)经右侧镀银面第一次反射恰能沿原路返回,说明折射光垂直于右侧镀银面,其光路如图所示。
设光在A点射入玻璃,入射到右侧镀银面的B点,并按原路返回
由题意可知:
由折射定律得:
解得,
设球冠的球心为O,对三角形OAS:
所以,三角形OAS为等腰三角形。
光源S与球冠顶点M之间的距离:
(2)
光在玻璃中的传播时间为
解得:
16.①15°②
【解析】
【详解】
①如图,透明物体内部的光路为折线,、点相对于底面对称,、和三点共线,在点处,光的入射角为,折射角为,,,根据题意有
由几何关系得,,于是,且得
②根据折射率公式有得
17.(1) (2)
【解析】
(i)由题,作出的光路如图所示
光在E点发生反射,光在F点发生折射,由反射定律得:
因AEF为等边三角形,则,光沿垂直AB面方向射出,则
根据折射定律得:
解得:
(ii)光在介质中的传播速度
由几何关系可得:,
光在介质中的传播时间
解得:
【点睛】先根据题意作出光路图,再根据几何关系求出入射角和折射角,根据折射定律求出折射率,根据求出光在介质中的速度,由几何关系求出光传播的路程,从而求光在介质中运动的时间.
18.(1);(2)。
【解析】
【分析】
【详解】
(1)当光线在球面发生全反射,即入射角为临界角C时,入射光线到光轴距离最大,由
解得
(2)由折射定律可得
由三角函数定义
由正弦定理
联立解得
距光轴的入射光线经球面折射后与光轴的交点到O点的距离为。
1.用波长为的平行单色光照射双缝,在光屏上偏离中心的P点处恰好出现亮条纹,则( )
A.改用波长为2的单色光照射,P点处一定出现亮条纹
B.改用波长为的单色光照射,P点处—定出现亮条纹
C.改用波长为2的单色光照射,P点处一定出现暗条纹
D.改用波长为的单色光照射,P点处一定出现暗条纹
2.一束单色光从空气射向某种介质的表面,光路如图所示。则该介质的折射率为( )
A.2.00 B.0.50 C.0.58 D.1.73
3.在一次观察光的衍射实验中,观察到如图所示的清晰的亮暗相间的图样,那么障碍物是下列给出的( )
A.很小的不透明圆板
B.很大的中间有大圆孔的不透明挡板
C.很大的不透明圆板
D.很大的中间有小圆孔的不透明挡板
4.下列有关光学现象的说法正确的是( )
A.光从光密介质射入光疏介质,其频率不变,传播速度变小
B.光从光密介质射入光疏介质,若入射角大于临界角,则一定发生全反射
C.光的干涉、衍射现象证明了光具有波动性
D.做双缝干涉实验时,用红光替代紫光,相邻明条纹间距变小
5.下列说法正确的是( )
A.观测到某星球上A元素发出的光的频率大于地球上A元素发出的光的频率,则该星球正在靠近地球
B.自然光包含着垂直于传播方向上的沿一切方向振动的光,且沿各个方向振动的光的强度均相同
C.在岸边观察水中的鱼,鱼的实际深度比看到的要浅一些
D.在光的双缝干涉实验中,若仅将入射光由绿光改为红光,则干涉条纹间距变宽
E.若红光由真空进入折射率为n的介质中,则红光在介质中的波长与其在真空中的波长的比值为n
6.两束不同频率的平行单色光a、b分别由水射入空气发生如图所示的折射现象(α<β),下列说法正确的是________.
A.随着a、b入射角度的逐渐增加,a先发生全反射
B.水对a的折射率比水对b的折射率小
C.a、b在水中的传播速度va>vb
D.a、b入射角为0°时,没有光线射入空气中
7.对如图所示的图片、示意图或实验装置图,下列判断正确的是( )
A.甲图是小孔衍射的图样,也被称为“泊松亮斑”
B.乙图是薄膜干涉的应用,用来检测平面的平整程度
C.丙图是双缝干涉原理图,若P到S1、S2的路程差是半波长的偶数倍,则P处是亮纹
D.丁图是薄膜干涉现象的实验装置图,在附有肥皂膜的铁丝圈上,出现竖直干涉条纹
8.下列色散现象是通过干涉产生的是
A.在白光下观察肥皂泡呈现彩色
B.一束太阳光通过三棱镜在墙壁上呈现彩色光斑
C.两块玻璃砖叠放在一起,玻璃砖上表面出现彩色条纹
D.将两支铅笔并排放置,其直缝与日光灯平行,通过直缝看到彩色条纹
9.如图中方框区域内有一个位置可以任意摆放的全反射棱镜,其横截面是等腰直角三角形,光线1、2、3、4表示的是入射光线,经过棱镜后,相应的出射光线是、、、下图4种情况中,哪些是可能实现的( )
A. B.
C. D.
10.下列有关光学现象的说法正确的是 .
A.光从光疏介质射入光密介质,若入射角大于临界角,则一定发生全反射
B.做双缝干涉实验时,用红光替代紫光,相邻明条纹间距变大
C.在白光下观察肥皂泡,其表面的相邻各条纹是等间距的
D.光的偏振现象表明光是横波
E.在同一种物质中,波长越短的光传播速度越小
11.杨氏双缝干涉实验中,双缝距光屏8cm,现将光屏靠近双缝,屏上原来3级亮纹依旧为亮纹,则移动的距离可能为( )
A.4.8 B.4 C.3.4 D.3
12.如图所示,是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于放置的光屏,沿方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
A.该玻璃体对A光的折射率比对B光的折射率小
B.A光的频率比B光的频率高
C.在该玻璃体中,A光比B光的波长长
D.在真空中,A光的波长比B光的波长长
E.A光从空气进入该玻璃体后,其频率变高
13.现有毛玻璃屏A、双缝B、白光光源C、单缝D、透红光的滤光片E等光学元件,要把它们放在图甲所示的光具座上组装成双缝干涉装置,用以测量红光的波长.
(1)本实验的步骤有:
①调节单缝与双缝的间距为5~10cm,并使单缝与双缝相互平行;
②按合理顺序在光具座上放置各光学元件,并使各元件的中心位于遮光筒的轴线上;
③取下遮光筒右侧的元件,打开光源,调节光源高度,使光束能直接沿遮光筒轴线把屏照亮;
④用米尺测出双缝到屏的距离;用测量头(读数方法同螺旋测微器)测量数条亮纹间的距离;
⑤将测得的数据代入公式求出红光的波长.
以上步骤合理的顺序是________.(只填步骤代号)
(2)将测量头的分划板中心刻线与某条亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图乙所示;然后同方向转动测量头,使分划板的中心刻线与第5条亮纹中心对齐,此时手轮上的示数如图丙所示.则图乙中手轮上的示数是________mm;图丙中手轮上的示数是________mm.
(3)已知双缝到屏的距离为0.500m,使用的双缝间距为2.8×10–4m,由此可求得所测红光波长为λ=________m(结果保留三位有效数字).
14.用双缝干涉测光的波长.实验装置如图(甲)所示,已知双缝与屏的距离L,双缝间距d.用测量头来测量亮纹中心的距离.测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心(如图(乙)所示),记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数.
(1)首先调节________和滤光片的中心位于遮光筒的中心轴线上,并使_________和________竖直且互相平行.
(2)分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如图(丙)所示,则对准第1条时读数x1=__________mm(允许误差)、对准第4条时读数x2=_______________mm(允许误差)
(3)写出计算波长λ的表达式,λ=______(用x1、 x2 、L 、d表示,不用计算).
15.有一玻璃球冠,右侧面镀银,光源S位于其对称轴上,如图所示.从光源S发出的一细光束射到球面上的A点,其反射光恰好垂直于球冠的对称轴,折射进入玻璃球冠内的光经右侧镀银面第一次反射后恰能沿原路返回.若球面半径为R,球冠高为,玻璃折射率为,光在真空中的传播速度为c.求:
(1)光源S与球冠顶点M之间的距离SM;
(2)光在玻璃中的传播时间.
16.一半圆柱形透明物体横截面如图所示,底面镀银,表示平圆截面的圆心,一束光线在横截面内从点入射,经过面反射后从点射出。已知光线在点的入射角为,,,求:
①光线在点的折射角;
②透明物体的折射率。
17.如图所示,直角三角形ABC为某种透明介质的横截面,∠B=30°,BC=30cm,AB面涂有反光材料.某单色光从BC上的D点垂直BC射入介质,经AB面反射后从AC面上射出,射出方向与AB面垂直.已知BD=21cm,不考虑光在AC面的反射.求:
(i)介质的折射率;
(ii)光在介质中的传播时间.
18.一半径为R的玻璃板球,O点是半球的球心,虚线OO?表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为,现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线,已知),求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
参考答案
1.B
【解析】
出现亮条纹是因为光程差为波长的整数倍,为n,如果n为奇数,当改用波长为2的单色光照射,P点的光程差为此时半波长的奇数倍,为暗条纹,因此AC错误,如果换成的单色光,则光程差一定为整数倍,则一定是亮条纹,B正确D错误
2.D
【解析】
由题单色光从空气射向该介质时,入射角,折射角,则该介质的折射率为
故D正确,ABC错误。
故选D。
3.D
【解析】
很大的中间有大圆孔的不透明挡板和很大的不透明圆板不会发生衍射现象,很小的不透明圆板出现泊松亮斑.
【详解】
A.用光照射很小的不透明圆板时后面出现一亮点,即泊松亮斑,故A错误;
B.很大的中间有大圆孔的不透明挡板时后面是一亮洞,不会出现衍射现象,故B错误;
C.很大的不透明圆板时后面是一片阴影,不会出现衍射现象,故C错误;
D.用光照射很大的中间有小圆孔的不透明挡板时是明暗相间的衍射图样,即发生衍射现象,故D正确.
【点睛】
该题考查单孔衍射的图样,要牢记单孔衍射和单缝衍射图样与障碍物或孔的尺寸是有关系的,不同的障碍物或孔出现的衍射图样是不一样的.
4.BC
【解析】
A.光从光密介质射入光疏介质,其频率不变,传播速度变大,选项A错误;
B.光从光密介质射入光疏介质,若入射角大于临界角,则一定发生全反射,选项B正确;
C.光的干涉、衍射现象证明了光具有波动性,选项C正确;
D.红光的波长大于紫光,做双缝干涉实验时,用红光替代紫光,根据可知,相邻明条纹间距变大,选项D错误。
故选BC。
5.ABD
【解析】
A.根据多普勒效应可以计算出物体相对运动的速度,所以通过测量星球上某些元素发出光波的频率,然后与地球上这些元素静止时发光的频率对照,就可以算出星球靠近或远离我们的速度,故A与题意相符;
B.自然光包含着垂直于传播方向上的沿一切方向振动的光,且沿各个方向振动的光的强度均相同,故B与题意相符;
C.在岸边观察水中的鱼,看到的鱼是由于鱼发出的光线经过水面折射形成的虚像,根据折射定律知折射角大于入射角,所以看到的鱼比实际深度要浅一些,故C与题意不符;
D.根据双缝干涉的宽度公式:可知,在光的双缝干涉实验中,若仅将入射光由绿光改为红光,波长变长,则干涉条纹间距变宽,故D与题意相符;
E.红光由真空进入折射率为n的介质中,频率不变,则
得红光在介质中的波长与其在真空中的波长的比值
故E与题意不符。
6.BC
【解析】
A.由图知,α<β,所以随着a、b入射角度的逐渐增加,折射角均增大,b光的折射角先达到90°,即b光先发生全反射,故A错误.
B.由于α<β,由折射定律知,折射率na小于nb,故B正确.
C.由v=c/n知,在水中的传播速度关系为va>vb,故C正确.
D.当a、b入射角为0°时,光线不偏折进入空气中.故D错误.
故选BC.
7.BC
【解析】
A.甲图是小孔衍射的图样,而“泊松亮斑”是圆板衍射,故不是“泊松亮斑”,故A错误;
B.乙图是薄膜干涉的应用,用来检测平面的平整程度。若干涉条纹是直的干涉条纹则表明平面平整,故B正确;
C.图是双缝干涉原理图,若P到S1、S2的路程差是光的半波长的偶数倍,则P是亮纹,若P到S1、S2的路程差是光的半波长的奇数倍,则P是暗纹,故C正确;
D.丁图是薄膜干涉现象的实验装置图,在附有肥皂膜的铁丝圈上,出现水平干涉条纹,故D错误。
故选BC。
8.AC
【解析】
A.肥皂泡在阳光下呈现彩色条纹是肥皂膜内外反射的光线,相互叠加产生的现象,这是光的干涉造成的,故A正确;
B.一束太阳光通过三棱镜在墙壁上呈现彩色光斑属于光的色散,B错误;
C.两块玻璃砖叠放在一起,玻璃砖上表面出现彩色条纹,时相互叠加产生的现象,这是光的干涉造成的,C正确;
D.两支铅笔并排放置,其直缝与日光灯平行,通过直缝看到彩色条纹,这是光的衍射现象,D错误.
故选AC。
9.ABC
【解析】
A.将全反射棱镜如图放置,可满足要求,选项A正确;
B. 将全反射棱镜如图放置,可满足要求,选项B正确;
C. 将全反射棱镜如图放置,可满足要求,选项C正确;
D. 全反射棱镜对光路有两种控制作用:将光的传播方向改变90°,或是改变180°,而没有会聚光线的作用,选项D选项错误。
10.BDE
【解析】
【详解】
A.全反射发生的条件是光从光密介质进入光疏介质,且入射角大于或等于临界角时,故A错误;
B.根据双缝干涉实验,相邻条纹间距,波长越长则干涉条纹间距越大,而红光的波长大于紫光波长,则红光的干涉条纹间距比紫光的大,故B正确;
C.根据以及不同颜色的光波长不同可知,不同颜色的光缠身的干涉条纹间距不同,故在白光下观察肥皂泡,其表面的相邻各条纹的间距是不等的,故C错误;
D.光的偏振现象证明了光是横波,纵波不能发生光的偏振现象,故D正确;
E.在同一种物质中,不同波长的光传播速度不同,波长越短,波速越小,故E正确.
11.ABCD
【解析】
【详解】
杨氏双缝干涉亮条纹的位置为
,k=0,±1,±2……
其中,d为双缝间距,D为双缝到光屏的距离,λ为光的波长。依题意有
,D
,k=4,5,6,……
带入D0=8cm可得D =6 cm,4.8 cm,4 cm,3.4 cm,3 cm……故ABCD均正确。
故选ABCD。
12.ACD
【解析】
【详解】
ABD.光线通过玻璃体后,A光的偏折程度比B光的小,则该玻璃体对A光的折射率比对B光的折射率小,而折射率越大,光的频率越高,说明A光的频率比B光的频率低,由c=λγ知,在真空中,A光的波长比B光的长,故A、D正确,B错误;
C.设同一光线在真空中的波长为λ0,在玻璃体中的波长为λ,折射率为n,则
,
得:
在真空中,A光的波长比B光的波长长,而玻璃体对A光的折射率比对B光的折射率小,由λ=λ0/n知,在该玻璃体中,A光比B光的波长长.故C正确;
E. 光的频率由光源决定,与介质无关,则A光从空气进入该玻璃体后,其频率不变.故E错误.
13.③②①④⑤ 1.130 5.580 6.23×10–7
【解析】
【分析】
【详解】
(1)[1]为获取单色线光源,白色光源后面要有滤光片、单缝、双缝.所以各光学元件的字母排列顺序应为③ ② ① ④ ⑤.
(2) [2][3]螺旋测微器乙的固定刻度读数为1mm,可动刻度读数为0.01×13.0mm=0.130mm,则最终读数为1.130mm.螺旋测微器丙的固定刻度读数为5.5mm,可动刻度读数为0.01×38.0mm=0.380mm,则最终读数为5.580mm.相邻条纹的间距
.
(3)[4]根据得
14.(1)光源 单缝 双缝 (2)2.190 7.869 (3)d(x2 –x1 )/3L
【解析】
(1)首先调节光源和滤光片的中心位于遮光筒的中心轴线上,并使单缝和双缝竖直且互相平行.
(2)图丙中固定刻度读数为2mm,可动刻度读数为0.01×19.0=0.190mm,所以最终读数为2.190mm.
对准第4条亮纹时固定刻度读数为7.5mm,可动读数为0.01×36.9=0.369mm,所以最终读数为7.869mm.
(3)根据得:
点睛:解决本题的关键掌握螺旋测微器的读数方法,固定刻度读数加上可动刻度读数,不需估读.以及掌握条纹间距公式.
15.(1),(2)
【解析】
【分析】
考查折射定律,光的传播。
【详解】
(1)经右侧镀银面第一次反射恰能沿原路返回,说明折射光垂直于右侧镀银面,其光路如图所示。
设光在A点射入玻璃,入射到右侧镀银面的B点,并按原路返回
由题意可知:
由折射定律得:
解得,
设球冠的球心为O,对三角形OAS:
所以,三角形OAS为等腰三角形。
光源S与球冠顶点M之间的距离:
(2)
光在玻璃中的传播时间为
解得:
16.①15°②
【解析】
【详解】
①如图,透明物体内部的光路为折线,、点相对于底面对称,、和三点共线,在点处,光的入射角为,折射角为,,,根据题意有
由几何关系得,,于是,且得
②根据折射率公式有得
17.(1) (2)
【解析】
(i)由题,作出的光路如图所示
光在E点发生反射,光在F点发生折射,由反射定律得:
因AEF为等边三角形,则,光沿垂直AB面方向射出,则
根据折射定律得:
解得:
(ii)光在介质中的传播速度
由几何关系可得:,
光在介质中的传播时间
解得:
【点睛】先根据题意作出光路图,再根据几何关系求出入射角和折射角,根据折射定律求出折射率,根据求出光在介质中的速度,由几何关系求出光传播的路程,从而求光在介质中运动的时间.
18.(1);(2)。
【解析】
【分析】
【详解】
(1)当光线在球面发生全反射,即入射角为临界角C时,入射光线到光轴距离最大,由
解得
(2)由折射定律可得
由三角函数定义
由正弦定理
联立解得
距光轴的入射光线经球面折射后与光轴的交点到O点的距离为。
同课章节目录
- 第一章机械振动
- 1.1研究简谐运动
- 1.2探究物体做简谐运动的原因
- 1.3探究摆钟的物理原理
- 1.4探究单摆振动的周期
- 1.5受迫振动与共振
- 第二章机械波
- 2.1 机械波的产生
- 2.2 机械波的描述
- 2.3机械波的案例分析
- 2.4惠更斯原理 波的反射与折射
- 2.5波的干涉与衍射
- 2.6多普勒效应
- 第三章电磁场与电磁波
- 3.1麦克斯韦的电磁场理论
- 3.2电磁波的发现
- 3.3无线电通信
- 3.4电磁波家族
- 第四章光的波动性
- 4.1光的干涉
- 4.2用双缝干涉仪测定光的波长
- 4.3光的衍射
- 4.4光的偏振与立体电影
- 4.5光的折射
- 4.6全反射与光导纤维
- 4.7激光
- 第五章新时空观的确立
- 5.1电磁场理论引发的怪异问题
- 5.2狭义相对论的基本原理
- 5.3奇特的相对论效应
- 5.4走近广义相对论
- 5.5无穷的宇宙
