北师大版六年级上册数学教案-总复习 整理复习稍复杂分数应用题
文档属性
| 名称 | 北师大版六年级上册数学教案-总复习 整理复习稍复杂分数应用题 |

|
|
| 格式 | doc | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览


文档简介
整理复习稍复杂分数应用题 教案
教学内容:稍复杂的分数、百分数解决问题常用的解题策略。
学情分析:
通过对分数乘法、分数除法、分数混合运算、百分数、百分数的应用、比进行学习后,学生对于简单的分数、百分数应用题能够正确解答。其次,基于上一节课学生对书上相关例题整理分类后,在将书由“厚”变“薄”的过程中头脑里已经构建了分数、百分数的知识网络,理清了求部分量、对应分率、单位“1”的量这三类基本题型的等量关系,掌握了基本的解题方法。但对于单位一多,数量多、数量关系比较复杂、量率对应不明确这些稍复杂的分数以及百分数应用题时,分析能力比较薄弱,缺乏正确的解题策略。
题单完成情况:
教学目标:
在回顾、对比、辨析稍复杂分数问题的过程中,在总结归纳中发现解决稍复杂分数应用题的常用策略。
引导学生在对题目信息的分析过程中,发现复杂分数应用题的一些基本模型,在模型思想中培养学生分析问题的能力。
在生生互评、生生质疑的过程中,培养学生解决问题以及语言表达能力。
教学重点:梳理解稍复杂分数、百分数应用题时,常用的解题策略。
教学难点:对于不同的稍复杂分数、百分数应用题时,怎样选择合适的解题策略。
教学过程:
教学流程
教师行为 学生活动 设计意图
?一、 复习回顾
二、题单讲评
1、
量率对应
2、
统一单位“1”
3、画图分析分步骤求出单位“1
4、量多时,理清量与量之间
5、
对比小结
6、
方程解题
7、假设法解题
8、比与分数的统一
9、小结
师:分数应用题可以分几类,每一类对应的数量关系是什么?
师:我们已经复习了有关这3类问题中的一步、两步简单的分数应用题,今天我们一起来复习稍复杂的分数应用题。
师:解决问题的一般要求是什么?
师:带着这样的要求,我们一起来读一读第一题。
师:它与昨天复习的分数应用题相比复杂在哪里?
师:分率没有直接告诉,需要我们去求,怎么求?
师:也就是说你觉得解决这道题的关键是什么?
师:也就是分析量率对应,找出量率对应,再利用这个等量关系就能可以解决这个问题。只是步骤多了一步而已。
假如天数再多一些,你还会算吗?
师:那第二题呢?一起读一读,对比一下与第一题有什么不同?
师:也就是说第一题是一个单位1,而第二题出现的多个单位1,从哪条信息看出来单位1不同?
师:余下的2/3你是怎么处理的?
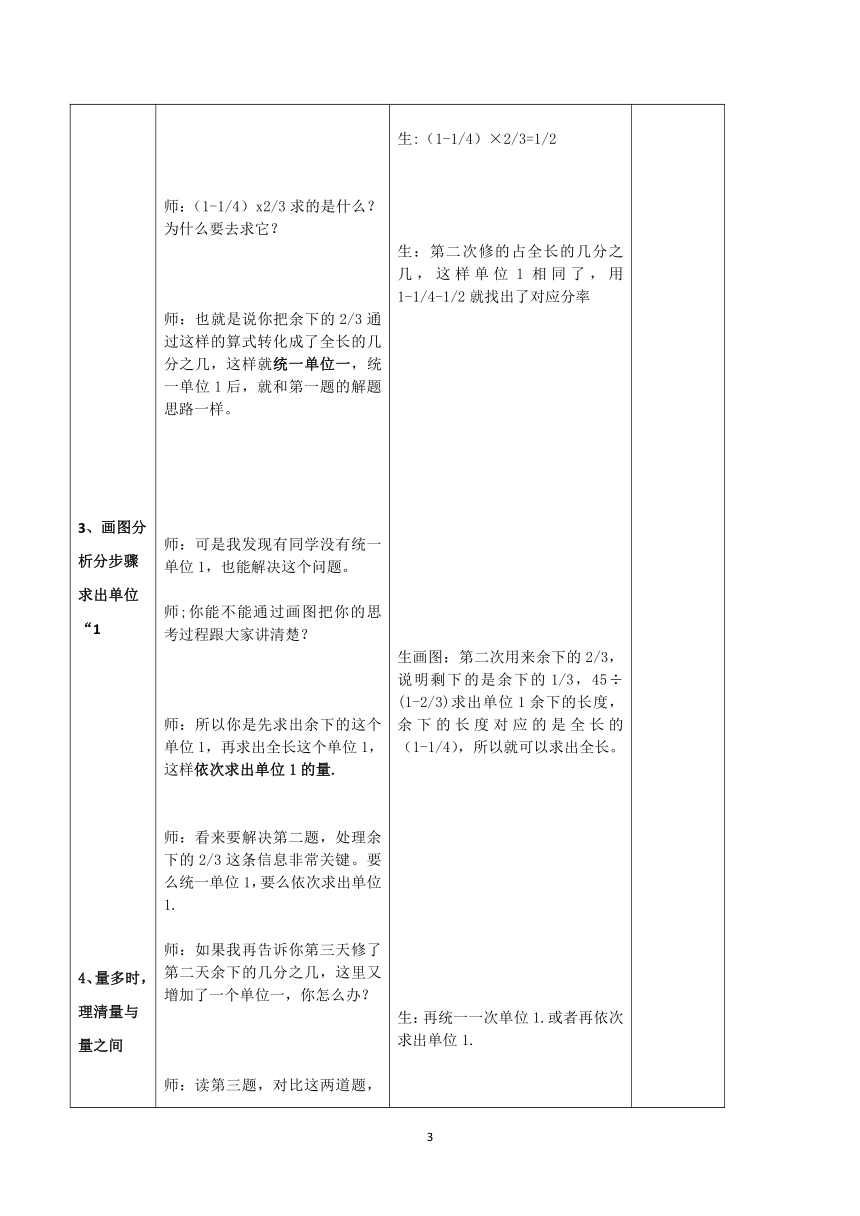
师:(1-1/4)x2/3求的是什么?为什么要去求它?
师:也就是说你把余下的2/3通过这样的算式转化成了全长的几分之几,这样就统一单位一,统一单位1后,就和第一题的解题思路一样。
师:可是我发现有同学没有统一单位1,也能解决这个问题。
师;你能不能通过画图把你的思考过程跟大家讲清楚?
师:所以你是先求出余下的这个单位1,再求出全长这个单位1,这样依次求出单位1的量.
师:看来要解决第二题,处理余下的2/3这条信息非常关键。要么统一单位1,要么依次求出单位1.
师:如果我再告诉你第三天修了第二天余下的几分之几,这里又增加了一个单位一,你怎么办?
师:读第三题,对比这两道题,有什么不同?
师:量多了怎么办?谁来说一说。
师:为什么要把5和45合在一起?你能在图上画一画吗?
师:看来第三题关键在这步,就是把5米和45米合在一起,产生一个新的部分量,这样就和我们第二题的解题方法完全相同。
师:现在我们回过头来看看这三道题,是从简单——复杂,仔细对比就会发现它们最后都在找出量率对应,利用这个等量关系求出单位1,只不过有些题率没有直接告诉我们,有些题量没有直接告诉我们。但只要我们抓住关键信息,就能化繁为简顺利解决这类稍复杂的分数应用题。
师:一起来读一读第4题,这道题,你勾画的单位1有哪些?属于三类问题的哪一类?
师:老师在批改的时候发现很多同学是用方程来解决的,我们前面整理的3道题都在求单位1,大家都是通过找量率对应,用除法求出单位1,那这道题你们为什么不用除法,要用方程?
师:你是怎样用方程解决这道题的?
师;也就是说当这种量多率多,单位1多,量率对应不好找的时候,我们就要转化策略,找出数量关系,用方程解决。
是不是就只能用方程解决呢?老师发现有十多个同学用算术方法仍然解决这个问题,我们来听一听他们怎么说?
师:其实这在数学上叫做假设法,
我们以前学什么知识用到过假设法?
师:看来假设法不仅可以解决鸡兔同笼问题,还可以解决分数问题。
师:听了这位同学的假设法你有什么感觉?
师:看来在解决稍复杂的题目的时候我们还可以选择我们很好理解的方法来解题,比如方程
师:现在来看看第5题。这道题和之前的题又有什么明显的区别?
师:当一个题里即出现了分数又出现了比,你是怎么处理的?
师:所以当分数应用题里即出现了分数又出现了比,我们要么把分数化成比,要么把比化成分数,也就是要统一比与分数。
师:你是怎么把比转化成了分数?
师:为什么是4/5,不是1/4呢?
师:也就是说转化成分数后,如果单位一不同,我们仍然要统一单位1,这样就变成了昨天我们复习的两步简单的分数问题。
师:你是把分数转化成了比,你是怎么转化的?
师:那你为什么要把总份数统一成15份呢?
师:每一份的量相同了再按比例分配,就能解决这个题目了。
师:其实这些都是我们解决问题的策略,今天我们又一起复习了稍复杂分数应用题,你有什么收获?
生:分三类:求单位“1”的量=用部分量÷对应分率;求部分量=“1”的量×对应分率;求分率=部分量÷单位“1”的量
生:审题、勾画单位1
生:分率没有直接告诉
生:用全长1-第一天的1/4-第二天的1/2就得到剩下的45的分率,1-1/4-1/2
生:找45对应的分率
生:会,再去掉第三天的分率。
生:第1题单位一相同,第二题单位一不同一个是全长,一个是剩余的
生:余下的2/3
生:(1-1/4)×2/3=1/2
生:第二次修的占全长的几分之几,这样单位1相同了,用1-1/4-1/2就找出了对应分率
生画图:第二次用来余下的2/3,说明剩下的是余下的1/3,45÷(1-2/3)求出单位1余下的长度,余下的长度对应的是全长的(1-1/4),所以就可以求出全长。
生:再统一一次单位1.或者再依次求出单位1.
生:多了一个5m
生:将5和45合在一起
生动手
生:求单位1。
生:量率对应不好找
生1、我用的是方程,把第一天徒弟设为X个,那第一天的师傅就有225-x个。再利用每个人第二天与第一天的数量关系,表示出第二天他们的数量,最后利用等量关系第二天的师傅个数+第二天的徒弟个数=300
生:假设乙第二天也比第一天多24%,那么第二天师徒总和比第一天总和多24%,也就是225X(1+24%)=279(个),但实际上总和为300,那是因为乙不止多增加了24%,他实际增加的是45%,而300—279对应的分率就是45%-24%,,这样就求出单位“1”乙第一天完成的量,进而算出第二天,乙的数量。
生:鸡兔同笼
生:听不懂
生:有比
生1:把比化成分数
生2:把分数化成比
生:4:1转化成4/5
生:。。。。
生:2/3就是已做与总座位的比为2:3。
生;这样才能统一每一份的量。
复习旧知为这节课的整理复习做铺垫
让学生体会分数应用题的解题关键就在于找量率对应。
梳理出单位1不同时,解题常用的策略。
通过改编题目,体会复杂题目与简单题目的联系,能够找到复杂题目的基本模型
让学生体会这些事常用策略,如果行不通要学会转化策略,体会转化思想的重要性。
学会根据题目信息,联想出许多相关联的信息,选择需要的信息来解决问题。
三、巩固应用 1、小红用三天读一本书,第一天读了全书的2/5,第二天读了余下的1/3,第三天读了60页,全书共多少页?
某村修一条公路,第一天修了全长的1/4多50米,第二天修了全长的1/3少5米刚好修完,全长共多少米?
甲、乙、丙三人共同加工一批零件,甲加工的数量与乙丙加工之和的比为1:3,乙加工的个数是甲和丙总和的1/3,丙加工了45个,这批零件共有多少个?
师:今天通过整理复习,大家有这么多收获,那以后我们遇到分数应用题的时候,要懂得具体问题具体分析,选择正确的策略来解决。(勾画)
教学内容:稍复杂的分数、百分数解决问题常用的解题策略。
学情分析:
通过对分数乘法、分数除法、分数混合运算、百分数、百分数的应用、比进行学习后,学生对于简单的分数、百分数应用题能够正确解答。其次,基于上一节课学生对书上相关例题整理分类后,在将书由“厚”变“薄”的过程中头脑里已经构建了分数、百分数的知识网络,理清了求部分量、对应分率、单位“1”的量这三类基本题型的等量关系,掌握了基本的解题方法。但对于单位一多,数量多、数量关系比较复杂、量率对应不明确这些稍复杂的分数以及百分数应用题时,分析能力比较薄弱,缺乏正确的解题策略。
题单完成情况:
教学目标:
在回顾、对比、辨析稍复杂分数问题的过程中,在总结归纳中发现解决稍复杂分数应用题的常用策略。
引导学生在对题目信息的分析过程中,发现复杂分数应用题的一些基本模型,在模型思想中培养学生分析问题的能力。
在生生互评、生生质疑的过程中,培养学生解决问题以及语言表达能力。
教学重点:梳理解稍复杂分数、百分数应用题时,常用的解题策略。
教学难点:对于不同的稍复杂分数、百分数应用题时,怎样选择合适的解题策略。
教学过程:
教学流程
教师行为 学生活动 设计意图
?一、 复习回顾
二、题单讲评
1、
量率对应
2、
统一单位“1”
3、画图分析分步骤求出单位“1
4、量多时,理清量与量之间
5、
对比小结
6、
方程解题
7、假设法解题
8、比与分数的统一
9、小结
师:分数应用题可以分几类,每一类对应的数量关系是什么?
师:我们已经复习了有关这3类问题中的一步、两步简单的分数应用题,今天我们一起来复习稍复杂的分数应用题。
师:解决问题的一般要求是什么?
师:带着这样的要求,我们一起来读一读第一题。
师:它与昨天复习的分数应用题相比复杂在哪里?
师:分率没有直接告诉,需要我们去求,怎么求?
师:也就是说你觉得解决这道题的关键是什么?
师:也就是分析量率对应,找出量率对应,再利用这个等量关系就能可以解决这个问题。只是步骤多了一步而已。
假如天数再多一些,你还会算吗?
师:那第二题呢?一起读一读,对比一下与第一题有什么不同?
师:也就是说第一题是一个单位1,而第二题出现的多个单位1,从哪条信息看出来单位1不同?
师:余下的2/3你是怎么处理的?
师:(1-1/4)x2/3求的是什么?为什么要去求它?
师:也就是说你把余下的2/3通过这样的算式转化成了全长的几分之几,这样就统一单位一,统一单位1后,就和第一题的解题思路一样。
师:可是我发现有同学没有统一单位1,也能解决这个问题。
师;你能不能通过画图把你的思考过程跟大家讲清楚?
师:所以你是先求出余下的这个单位1,再求出全长这个单位1,这样依次求出单位1的量.
师:看来要解决第二题,处理余下的2/3这条信息非常关键。要么统一单位1,要么依次求出单位1.
师:如果我再告诉你第三天修了第二天余下的几分之几,这里又增加了一个单位一,你怎么办?
师:读第三题,对比这两道题,有什么不同?
师:量多了怎么办?谁来说一说。
师:为什么要把5和45合在一起?你能在图上画一画吗?
师:看来第三题关键在这步,就是把5米和45米合在一起,产生一个新的部分量,这样就和我们第二题的解题方法完全相同。
师:现在我们回过头来看看这三道题,是从简单——复杂,仔细对比就会发现它们最后都在找出量率对应,利用这个等量关系求出单位1,只不过有些题率没有直接告诉我们,有些题量没有直接告诉我们。但只要我们抓住关键信息,就能化繁为简顺利解决这类稍复杂的分数应用题。
师:一起来读一读第4题,这道题,你勾画的单位1有哪些?属于三类问题的哪一类?
师:老师在批改的时候发现很多同学是用方程来解决的,我们前面整理的3道题都在求单位1,大家都是通过找量率对应,用除法求出单位1,那这道题你们为什么不用除法,要用方程?
师:你是怎样用方程解决这道题的?
师;也就是说当这种量多率多,单位1多,量率对应不好找的时候,我们就要转化策略,找出数量关系,用方程解决。
是不是就只能用方程解决呢?老师发现有十多个同学用算术方法仍然解决这个问题,我们来听一听他们怎么说?
师:其实这在数学上叫做假设法,
我们以前学什么知识用到过假设法?
师:看来假设法不仅可以解决鸡兔同笼问题,还可以解决分数问题。
师:听了这位同学的假设法你有什么感觉?
师:看来在解决稍复杂的题目的时候我们还可以选择我们很好理解的方法来解题,比如方程
师:现在来看看第5题。这道题和之前的题又有什么明显的区别?
师:当一个题里即出现了分数又出现了比,你是怎么处理的?
师:所以当分数应用题里即出现了分数又出现了比,我们要么把分数化成比,要么把比化成分数,也就是要统一比与分数。
师:你是怎么把比转化成了分数?
师:为什么是4/5,不是1/4呢?
师:也就是说转化成分数后,如果单位一不同,我们仍然要统一单位1,这样就变成了昨天我们复习的两步简单的分数问题。
师:你是把分数转化成了比,你是怎么转化的?
师:那你为什么要把总份数统一成15份呢?
师:每一份的量相同了再按比例分配,就能解决这个题目了。
师:其实这些都是我们解决问题的策略,今天我们又一起复习了稍复杂分数应用题,你有什么收获?
生:分三类:求单位“1”的量=用部分量÷对应分率;求部分量=“1”的量×对应分率;求分率=部分量÷单位“1”的量
生:审题、勾画单位1
生:分率没有直接告诉
生:用全长1-第一天的1/4-第二天的1/2就得到剩下的45的分率,1-1/4-1/2
生:找45对应的分率
生:会,再去掉第三天的分率。
生:第1题单位一相同,第二题单位一不同一个是全长,一个是剩余的
生:余下的2/3
生:(1-1/4)×2/3=1/2
生:第二次修的占全长的几分之几,这样单位1相同了,用1-1/4-1/2就找出了对应分率
生画图:第二次用来余下的2/3,说明剩下的是余下的1/3,45÷(1-2/3)求出单位1余下的长度,余下的长度对应的是全长的(1-1/4),所以就可以求出全长。
生:再统一一次单位1.或者再依次求出单位1.
生:多了一个5m
生:将5和45合在一起
生动手
生:求单位1。
生:量率对应不好找
生1、我用的是方程,把第一天徒弟设为X个,那第一天的师傅就有225-x个。再利用每个人第二天与第一天的数量关系,表示出第二天他们的数量,最后利用等量关系第二天的师傅个数+第二天的徒弟个数=300
生:假设乙第二天也比第一天多24%,那么第二天师徒总和比第一天总和多24%,也就是225X(1+24%)=279(个),但实际上总和为300,那是因为乙不止多增加了24%,他实际增加的是45%,而300—279对应的分率就是45%-24%,,这样就求出单位“1”乙第一天完成的量,进而算出第二天,乙的数量。
生:鸡兔同笼
生:听不懂
生:有比
生1:把比化成分数
生2:把分数化成比
生:4:1转化成4/5
生:。。。。
生:2/3就是已做与总座位的比为2:3。
生;这样才能统一每一份的量。
复习旧知为这节课的整理复习做铺垫
让学生体会分数应用题的解题关键就在于找量率对应。
梳理出单位1不同时,解题常用的策略。
通过改编题目,体会复杂题目与简单题目的联系,能够找到复杂题目的基本模型
让学生体会这些事常用策略,如果行不通要学会转化策略,体会转化思想的重要性。
学会根据题目信息,联想出许多相关联的信息,选择需要的信息来解决问题。
三、巩固应用 1、小红用三天读一本书,第一天读了全书的2/5,第二天读了余下的1/3,第三天读了60页,全书共多少页?
某村修一条公路,第一天修了全长的1/4多50米,第二天修了全长的1/3少5米刚好修完,全长共多少米?
甲、乙、丙三人共同加工一批零件,甲加工的数量与乙丙加工之和的比为1:3,乙加工的个数是甲和丙总和的1/3,丙加工了45个,这批零件共有多少个?
师:今天通过整理复习,大家有这么多收获,那以后我们遇到分数应用题的时候,要懂得具体问题具体分析,选择正确的策略来解决。(勾画)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
