上海市甘泉高中2019-2020学年高中物理物理沪科版选修3-4:光的波动性 单元测试题(含解析)
文档属性
| 名称 | 上海市甘泉高中2019-2020学年高中物理物理沪科版选修3-4:光的波动性 单元测试题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-23 09:38:38 | ||
图片预览




文档简介
光的波动性
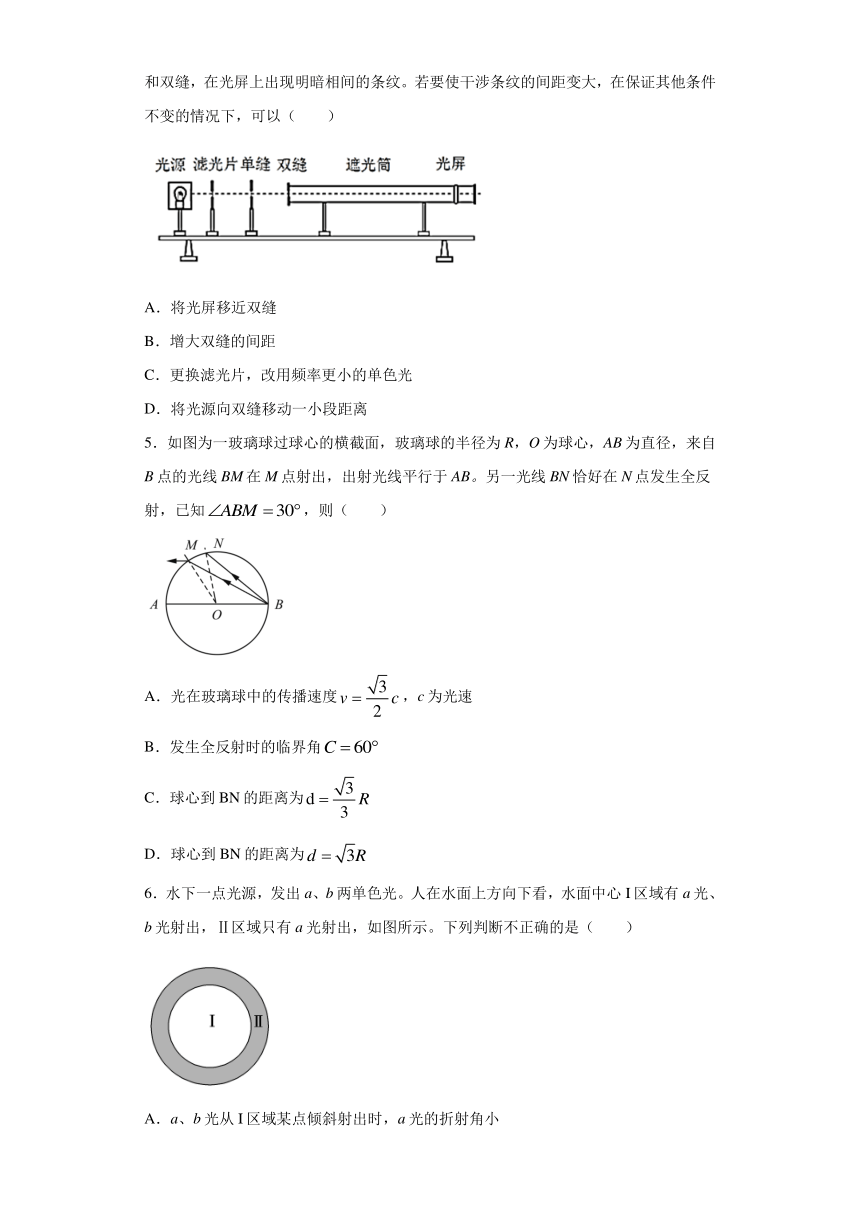
1.如图所示,一束激光照射在双缝上,在缝后屏上得到干涉条纹,下列说法中正确的是( )
A.增大双缝到光屏的距离,条纹间距变小
B.入射光波长不变,光强增大,条纹间距不变
C.增大激光器到双缝的距离,条纹间距变大
D.若仅将双缝和光屏置于水中,同等条件下条纹间距变大
2.如图所示,用单色光做双缝干涉实验,P为第二条亮条纹,改用频率较高的单色光再做实验(其他不变)时,则第二个亮条纹的位置
A.仍在P点
B.在P点上方
C.在P点下方
D.要将屏向双缝方向移近一些才能看到亮条纹
3.图1是研究光的干涉现象的装置示意图,在光屏P上观察到的图样如图2所示。为了增大条纹间的距离,下列做法正确的是( )
A.增大单色光的频率
B.增大双缝屏上的双缝间距
C.增大双缝屏到光屏的距离
D.增大单缝屏到双缝屏的距离
4.如图为双缝干涉的实验示意图,光源发出的光经滤光片成为单色光,然后通过单缝和双缝,在光屏上出现明暗相间的条纹。若要使干涉条纹的间距变大,在保证其他条件不变的情况下,可以( )
A.将光屏移近双缝
B.增大双缝的间距
C.更换滤光片,改用频率更小的单色光
D.将光源向双缝移动一小段距离
5.如图为一玻璃球过球心的横截面,玻璃球的半径为R,O为球心,AB为直径,来自B点的光线BM在M点射出,出射光线平行于AB。另一光线BN恰好在N点发生全反射,已知,则( )
A.光在玻璃球中的传播速度,c为光速
B.发生全反射时的临界角
C.球心到BN的距离为
D.球心到BN的距离为
6.水下一点光源,发出a、b两单色光。人在水面上方向下看,水面中心I区域有a光、b光射出,Ⅱ区域只有a光射出,如图所示。下列判断不正确的是( )
A.a、b光从I区域某点倾斜射出时,a光的折射角小
B.在真空中,a光的波长大于b光的波长
C.水对a光的折射率大于对b光的折射率
D.水下a、b光能射到图中I区域以外区域
7.如图所示是某一单色光由空气射入截面为等腰梯形的玻璃砖,或由该玻璃砖射入空气时的光路图,其中正确的是( )(已知该玻璃砖对该单色光的折射率为1.5)
A.图甲、图丙 B.图甲、图丁 C.图乙、图丙 D.图乙、图丁
8.已知天然材料的折射率都为正值()。近年来,人们针对电磁波某些频段设计的人工材料,可以使折射率为负值(),称为负折射率介质。电磁波从正折射率介质入射到负折射介质时,符合折射定律,但折射角为负,即折射线与入射线位于界面法线同侧,如图所示。点波源S发出的电磁波经一负折射率平板介质后,在另一侧成实像。如图2所示,其中直线SO垂直于介质平板,则图中画出的4条折射线(标号为1、2、3、4)之中,正确的是( )
A.1 B.2 C.3 D.4
9.如图所示。有一束平行于等边三棱镜横截面ABC的红光从空气射向E点,并偏折到F点。已知入射方向与边AB的夹角,E.F分别为边AB.BC的中点,则( )
A.该三棱镜对红光的折射率为
B.光在F点发生全反射
C.从F点出射的光束与入射到E点的光束的夹角为
D.若改用紫光沿相同角度从E点入射,则出射点在F点左侧
10.如图所示,两束单色光a、b从水下面射向A点,光线经折射后合成一束光c,则下列说法正确的是__________
A.用同一双缝干涉实验装置分别以a、b光做实验,a光的干涉条纹间距大于b光的干涉条纹间距
B.a比b更容易发生衍射现象
C.在水中a光的速度比b光的速度小
D.在水中a光的临界角大于b光的临界角
E.若a光与b光以相同入射角从水射向空气,在不断增大入射角时水面上首先消失的是a光
11.如图所示,足够长的平行玻璃砖厚度为d,底面镀有反光膜CD,反光膜厚度不计,一束光线以45°的入射角由A点入射,经底面反光膜反射后,从顶面B点射出(B点图中未画出).已知该光线在玻璃砖中的传播速度为c,c为光在真空中的传播速度,则( )
A.平行玻璃砖的折射率为
B.入射点A与出射点B之间的距离为
C.平行玻璃砖的全反射临界角为30°
D.为了使从A点以各种角度入射的光线都能从顶面射出,则底面反光膜CD长度至少2d
12.为了研究某种透明新材料的光学性质,将其压制成半圆柱形,如图甲所示。一束激光由真空沿半圆柱体的径向与其底面过O的法线成θ角射人。CD为光学传感器,可以探测光的强度。从AB面反射回来的光强随角θ变化的情况如图乙所示。现在将这种新材料制成的一根光导纤维束弯成半圆形,暴露于空气中(假设空气中的折射率与真空相同),设半圆形外半径为R,光导纤维束的半径为r。则下列说法正确的是
A.该新材料的折射率n> 1
B.该新材料的折射率n<1
C.图甲中若减小入射角θ,则反射光线和折射光线之间的夹角也将变小
D.用同种激光垂直于光导纤维束端面EF射入,如图丙。若该束激光不从光导纤维束侧面外泄,则弯成的半圆形半径R与纤维束半径r应满足的关系为
13.游标为20分度的卡尺示数如图所示,此时两测脚间狭缝的宽度为__________mm.用激光照射该狭缝,在屏上出现衍射条纹。如果减小狭缝的宽度,衍射条纹的宽度将变____________.
14.某同学利用“插针法”测定平行玻璃砖的折射率,在坐标纸上记录的情况如图所示,虚线为以入射点O为圆心做出的圆,由此计算出玻璃砖的折射率为_________,光在玻璃中的传播速度为________m/s.(光在真空中的传播速度为,结果均保留两位有效数字)
15.如图所示,一截面为正三角形的棱镜,其折射率为.今有一束单色光射到它的一个侧面,经折射后与底边平行,再射向另一侧面后射出.求:
①光第一次射到棱镜侧面时的入射角大小
②出射光线相对于第一次射向棱镜的入射光线偏转的角度
16.如图所示,一束平行紫光垂直射向半径为的横截面为扇形的玻璃砖薄片(其右侧涂有吸光物质),经折射后在屏幕S上形成一亮区,已知屏幕S至球心距离为,玻璃半球对紫光的折射率为,不考虑光的干涉和衍射。求:
(1)若某束光线在玻璃砖圆弧面入射角,其折射角α;
(2)亮区右边界到P点的距离d。
17.如图,O1O2为经过球形透明体的直线,平行光束沿O1O2方向照射到透明体上。已知透明体的半径为R,真空中的光速为c。
(1)不考虑光在球内的反射,若光通过透明体的最长时间为t,求透明体材料的折射率;
(2)若透明体材料的折射率为,求以45°的入射角射到A点的光,通过透明体后与O1O2的交点到球心O的距离。
18.如图所示,半径为 R 的透明半球体放在水平桌面上方,O 为球心,直径恰好水平,轴线 OO'垂直于水平桌面。位于O点正上方某一高度处的点光源 S,发出一束单色光,射向半球体上的A点,已知入射角α=60°,光在真空中传播速度为C,透明半球体对该单色光的折射率为,该束光通过半球体后刚好垂直射到桌面上 P 点,不考虑半球体内光的反射,求:
(ⅰ)点 P 距离点O'的距离 l
(ⅱ)该光束在透明半球体内传播的时间
参考答案
1.B
【解析】
干涉条纹中相邻两个两条纹或暗条纹的中心间距为
A.增大双缝到光屏的距离,即增大l,条纹间距变大,所以A错误;
B.入射光波长不变,光强增大,不会改变条纹间距,即条纹间距不变,所以B正确;
C.条纹间距与激光器到双缝的距离无关,所以增大激光器到双缝的距离,条纹间距不变,所以C错误;
D.若仅将双缝和光屏置于水中,光在介质中的折射率变大,根据
可知,光的传播速度变小,频率不变,则根据
可知,光的波长变短,则条纹间距变小,所以D错误。
故选B。
2.C
【解析】
ABC.频率增大,则波长变小,根据双缝干涉条纹的间距公式
可知,相邻条纹的间距变小,则第二条暗纹的中点在P点的下方.故AB错误,C正确;
D.当改用频率较高的单色光,则波长变小时,出现明(暗)条纹的间距宽度变小,若将屏向双缝方向远离一些即可看到第二个亮条纹的位置,故D错误.
故选C.
3.C
【解析】
A.增大单色光频率,则波长减小,根据公式可知,条纹间的距离减小,A不符合要求;
B.增大双缝屏上的双缝间距d,根据公式可知,条纹间的距离减小,B不符合要求;
C.增大双缝屏到光屏的距离L,根据公式可知,条纹间的距离增大,C符合要求;
D.根据公式可知,条纹间的距离与单缝屏到双缝屏的距离无关,D不符合要求。
故选C。
4.C
【解析】
实验中用激光通过双缝,双缝的作用是形成相干光源;由干涉条纹间距
知为了增大光屏上干涉条纹的间距,应使得双缝间距离d缩小,或者增大L与λ;
A.将光屏移近双缝,则L减小,不符合要求,故A错误;
B.增大双缝的间距d,导致条纹间距变小,故B错误;
C.换滤光片,改用频率更小即波长更长的单色光,符合要求,故C正确;
D.光源向双缝移动一小段距离,不会影响条纹间距,故D错误。
故选C。
5.C
【解析】
A.已知,由几何关系知入射角,折射角 ,则玻璃的折射率为
光在玻璃中传播速度
A错误;
B.发生全反射的临界角
因为
B错误;
CD.因为光线BN恰好在N点发生全反射,球心到光线BN的距离为
D错误C正确。
故选C。
6.C
【解析】
AC.由题分析可知,b光在I区域边缘发生了全反射,a光Ⅱ区域边缘发生了全反射,则知a光的临界角比b光的临界角大,由知,水对a光的折射率小于对b光的折射率,由折射定律知:a、b光从I区域某点倾斜射出时,a光折射角小,故A正确,不符合题意,C错误,符合题意;
B.水对a光的折射率小于对b光的折射率,则a光的频率小于b光的频率,由c=λf知,在真空中,因光速c不变,则有a光的波长大于b光的波长。故B正确,不符合题意;
D.水下a、b光经水面反射后均能射到图中I区域以外区域,故D正确,不符合题意。
故选C。
7.C
【解析】
单色光由空气射入玻璃砖时,折射角小于入射角。图甲错误。图乙正确;当该单色光由玻璃砖射入空气时,发生全反射的临界角的正弦值
因为
所以临界角,图丙、图丁中该单色光由玻璃砖射入空气时的入射角为,大于临界角,会发生全反射,图丙正确,图丁错误。
故选C。
8.D
【解析】
ABCD.由题,点波源S发出的电磁波经一负折射率平板介质后,折射光线与入射光线在法线的同一侧,所以不可能是光学1或2;根据光线穿过两侧平行的介质后的特点:方向与开始时的方向相同,所以光线3出介质右侧后,根据折射光线与入射光线在法线同侧这一条件,光线将无法汇聚形成实像;光线4才能满足“同侧”+“成实像”的条件,所以折射光线4可能是正确的,光线3是错误的,由以上的分析可知,ABC错误D正确。
故选D。
9.AC
【解析】
A.如图所示,作两界面法线相交于D点,在AB界面,由几何知识知,入射角为,折射角为,所以
故A正确;
B.光在BC界面上人射角为,则
即临界角
则在BC面上不会发生全反射,故B错误;
C.分析知BC面上折射角为,入射光线与出射光线相交于G点,,,则
,,
则
所以从F点出射的光束与入射到E点的光束的夹角为,故C正确;
D.紫光频率比红光频率大,棱镜对紫光的折射率大,若改用紫光沿相同角度从E点人射,则出射点在F点右侧,D错误。
故选AC。
10.ABD
【解析】
由图可知,单色光a偏折程度小于b的偏折程度,根据折射定律知,a光的折射率小于b光的折射率,则知a光的波长大.根据双缝干涉条纹的间距公式,可得,干涉条纹间距与波长成正比,所以a光的干涉条纹间距大于b光的干涉条纹间距,故A正确;a光的波长长,波动性强,更容易发生衍射现象,故B正确;由知,在水中a光的速度大,故C错误;由全反射临界角公式,知折射率n越大,临界角C越小,则知在水中a光的临界角大于b光的临界角,故D正确;若a光与b光以相同入射角从水射向空气时,由于在水中a光的临界角大于b光的临界角,所以b光的入射角先达到临界角,则b光先发生全反射,首先消失的是b光,故E错误.
11.ABD
【解析】
A.玻璃砖的折射率为
故A正确;
B.由折射定律得
可得
因此入射点与出射点之间的距离为
故B正确;
C.设临界角为,则有
可得
故C错误;
D.为了使从点以各种角度入射的光线都能从顶面射出,反射光线不能在顶面发生全反射,则底面反光膜至少为
故D正确;
故选ABD。
12.AD
【解析】
AB.由题图乙知,当时发生全反射,则有:
故选项A符合题意,B不符合题意;
C.图甲中若减小入射角,根据反射定律和折射定律可知反射角和折射角都减小,则反射光线和折射光线之间的夹角也将变大,故选项C不符合题意;
D.激光不从光导纤维束侧面外泄的临界条件是入射光在外侧面处发生全反射,临界光路如图所示,可得:
解得:,所以该束激光不从光导纤维束侧面外泄,则弯成的半圆形半径与纤维束半径应满足的关系为,故选项D符合题意。
13. 0.15 宽
【解析】游标卡尺的主尺读数为0mm,游标读数为0.05×3=0.15mm,所以最终读数为:0mm+0.15mm=0.15mm,根据条纹间距公式,可知当减小狭缝的宽度减小时,条纹间距变宽.
14.1.5 2.0×108
【解析】
(1)玻璃砖的折射率为
(2)光在玻璃中的传播速度
15.①60o② 60°
【解析】
①如图所示,在AB面发生折射,折射角r=30°,
由光的折射定律
则
i=60°
②因折射光线与底边BC平行,由光路可逆知第二次在AC面折射时的入射角为30°,折射角为60°,由几何关系可知
θ=2(i-30°)=60°
16.(1);(2)1m
【解析】
(1)据折射定律得
得
(2)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到G的距离d就是所求宽度。
设紫光临界角为,由全反射的知识得
得
中
得
中
得
17.(1);(2)。
【解析】
(1)光在透明体内的最长路径为2R,不考虑光在球内的反射,则有
透明体材料的折射率
;
(2)该光线的传播路径如图,入射角i=45°,折射率为n=,根据折射定律,则折射角r=30°
光从B点射出时的出射角为45°,由几何关系知,∠BOC=15°,∠BCO=30°,∠CBO=135°,由正弦定理,有
解得以45°的入射角射到A点的光,通过透明体后与O1O2的交点到球心O的距离
。
18.(i)(ii)
【解析】
(i)光从光源S射出经半球体到达水平桌面的光路如图
光由空气射向半球体,由折射定律,有
①
得
光束射出透明半球体,设入射角为,出射角设为,有
②
由几何关系有
③
联立②③得
由几何关系可知
④
得:
(ii)光在半球体中传播的速度为
⑤
得
由几何关系可知,为等腰三角形,光在透明半球体中传播的距离
⑥
得
该光束在透明半球体内传播的时间t
⑦
得
1.如图所示,一束激光照射在双缝上,在缝后屏上得到干涉条纹,下列说法中正确的是( )
A.增大双缝到光屏的距离,条纹间距变小
B.入射光波长不变,光强增大,条纹间距不变
C.增大激光器到双缝的距离,条纹间距变大
D.若仅将双缝和光屏置于水中,同等条件下条纹间距变大
2.如图所示,用单色光做双缝干涉实验,P为第二条亮条纹,改用频率较高的单色光再做实验(其他不变)时,则第二个亮条纹的位置
A.仍在P点
B.在P点上方
C.在P点下方
D.要将屏向双缝方向移近一些才能看到亮条纹
3.图1是研究光的干涉现象的装置示意图,在光屏P上观察到的图样如图2所示。为了增大条纹间的距离,下列做法正确的是( )
A.增大单色光的频率
B.增大双缝屏上的双缝间距
C.增大双缝屏到光屏的距离
D.增大单缝屏到双缝屏的距离
4.如图为双缝干涉的实验示意图,光源发出的光经滤光片成为单色光,然后通过单缝和双缝,在光屏上出现明暗相间的条纹。若要使干涉条纹的间距变大,在保证其他条件不变的情况下,可以( )
A.将光屏移近双缝
B.增大双缝的间距
C.更换滤光片,改用频率更小的单色光
D.将光源向双缝移动一小段距离
5.如图为一玻璃球过球心的横截面,玻璃球的半径为R,O为球心,AB为直径,来自B点的光线BM在M点射出,出射光线平行于AB。另一光线BN恰好在N点发生全反射,已知,则( )
A.光在玻璃球中的传播速度,c为光速
B.发生全反射时的临界角
C.球心到BN的距离为
D.球心到BN的距离为
6.水下一点光源,发出a、b两单色光。人在水面上方向下看,水面中心I区域有a光、b光射出,Ⅱ区域只有a光射出,如图所示。下列判断不正确的是( )
A.a、b光从I区域某点倾斜射出时,a光的折射角小
B.在真空中,a光的波长大于b光的波长
C.水对a光的折射率大于对b光的折射率
D.水下a、b光能射到图中I区域以外区域
7.如图所示是某一单色光由空气射入截面为等腰梯形的玻璃砖,或由该玻璃砖射入空气时的光路图,其中正确的是( )(已知该玻璃砖对该单色光的折射率为1.5)
A.图甲、图丙 B.图甲、图丁 C.图乙、图丙 D.图乙、图丁
8.已知天然材料的折射率都为正值()。近年来,人们针对电磁波某些频段设计的人工材料,可以使折射率为负值(),称为负折射率介质。电磁波从正折射率介质入射到负折射介质时,符合折射定律,但折射角为负,即折射线与入射线位于界面法线同侧,如图所示。点波源S发出的电磁波经一负折射率平板介质后,在另一侧成实像。如图2所示,其中直线SO垂直于介质平板,则图中画出的4条折射线(标号为1、2、3、4)之中,正确的是( )
A.1 B.2 C.3 D.4
9.如图所示。有一束平行于等边三棱镜横截面ABC的红光从空气射向E点,并偏折到F点。已知入射方向与边AB的夹角,E.F分别为边AB.BC的中点,则( )
A.该三棱镜对红光的折射率为
B.光在F点发生全反射
C.从F点出射的光束与入射到E点的光束的夹角为
D.若改用紫光沿相同角度从E点入射,则出射点在F点左侧
10.如图所示,两束单色光a、b从水下面射向A点,光线经折射后合成一束光c,则下列说法正确的是__________
A.用同一双缝干涉实验装置分别以a、b光做实验,a光的干涉条纹间距大于b光的干涉条纹间距
B.a比b更容易发生衍射现象
C.在水中a光的速度比b光的速度小
D.在水中a光的临界角大于b光的临界角
E.若a光与b光以相同入射角从水射向空气,在不断增大入射角时水面上首先消失的是a光
11.如图所示,足够长的平行玻璃砖厚度为d,底面镀有反光膜CD,反光膜厚度不计,一束光线以45°的入射角由A点入射,经底面反光膜反射后,从顶面B点射出(B点图中未画出).已知该光线在玻璃砖中的传播速度为c,c为光在真空中的传播速度,则( )
A.平行玻璃砖的折射率为
B.入射点A与出射点B之间的距离为
C.平行玻璃砖的全反射临界角为30°
D.为了使从A点以各种角度入射的光线都能从顶面射出,则底面反光膜CD长度至少2d
12.为了研究某种透明新材料的光学性质,将其压制成半圆柱形,如图甲所示。一束激光由真空沿半圆柱体的径向与其底面过O的法线成θ角射人。CD为光学传感器,可以探测光的强度。从AB面反射回来的光强随角θ变化的情况如图乙所示。现在将这种新材料制成的一根光导纤维束弯成半圆形,暴露于空气中(假设空气中的折射率与真空相同),设半圆形外半径为R,光导纤维束的半径为r。则下列说法正确的是
A.该新材料的折射率n> 1
B.该新材料的折射率n<1
C.图甲中若减小入射角θ,则反射光线和折射光线之间的夹角也将变小
D.用同种激光垂直于光导纤维束端面EF射入,如图丙。若该束激光不从光导纤维束侧面外泄,则弯成的半圆形半径R与纤维束半径r应满足的关系为
13.游标为20分度的卡尺示数如图所示,此时两测脚间狭缝的宽度为__________mm.用激光照射该狭缝,在屏上出现衍射条纹。如果减小狭缝的宽度,衍射条纹的宽度将变____________.
14.某同学利用“插针法”测定平行玻璃砖的折射率,在坐标纸上记录的情况如图所示,虚线为以入射点O为圆心做出的圆,由此计算出玻璃砖的折射率为_________,光在玻璃中的传播速度为________m/s.(光在真空中的传播速度为,结果均保留两位有效数字)
15.如图所示,一截面为正三角形的棱镜,其折射率为.今有一束单色光射到它的一个侧面,经折射后与底边平行,再射向另一侧面后射出.求:
①光第一次射到棱镜侧面时的入射角大小
②出射光线相对于第一次射向棱镜的入射光线偏转的角度
16.如图所示,一束平行紫光垂直射向半径为的横截面为扇形的玻璃砖薄片(其右侧涂有吸光物质),经折射后在屏幕S上形成一亮区,已知屏幕S至球心距离为,玻璃半球对紫光的折射率为,不考虑光的干涉和衍射。求:
(1)若某束光线在玻璃砖圆弧面入射角,其折射角α;
(2)亮区右边界到P点的距离d。
17.如图,O1O2为经过球形透明体的直线,平行光束沿O1O2方向照射到透明体上。已知透明体的半径为R,真空中的光速为c。
(1)不考虑光在球内的反射,若光通过透明体的最长时间为t,求透明体材料的折射率;
(2)若透明体材料的折射率为,求以45°的入射角射到A点的光,通过透明体后与O1O2的交点到球心O的距离。
18.如图所示,半径为 R 的透明半球体放在水平桌面上方,O 为球心,直径恰好水平,轴线 OO'垂直于水平桌面。位于O点正上方某一高度处的点光源 S,发出一束单色光,射向半球体上的A点,已知入射角α=60°,光在真空中传播速度为C,透明半球体对该单色光的折射率为,该束光通过半球体后刚好垂直射到桌面上 P 点,不考虑半球体内光的反射,求:
(ⅰ)点 P 距离点O'的距离 l
(ⅱ)该光束在透明半球体内传播的时间
参考答案
1.B
【解析】
干涉条纹中相邻两个两条纹或暗条纹的中心间距为
A.增大双缝到光屏的距离,即增大l,条纹间距变大,所以A错误;
B.入射光波长不变,光强增大,不会改变条纹间距,即条纹间距不变,所以B正确;
C.条纹间距与激光器到双缝的距离无关,所以增大激光器到双缝的距离,条纹间距不变,所以C错误;
D.若仅将双缝和光屏置于水中,光在介质中的折射率变大,根据
可知,光的传播速度变小,频率不变,则根据
可知,光的波长变短,则条纹间距变小,所以D错误。
故选B。
2.C
【解析】
ABC.频率增大,则波长变小,根据双缝干涉条纹的间距公式
可知,相邻条纹的间距变小,则第二条暗纹的中点在P点的下方.故AB错误,C正确;
D.当改用频率较高的单色光,则波长变小时,出现明(暗)条纹的间距宽度变小,若将屏向双缝方向远离一些即可看到第二个亮条纹的位置,故D错误.
故选C.
3.C
【解析】
A.增大单色光频率,则波长减小,根据公式可知,条纹间的距离减小,A不符合要求;
B.增大双缝屏上的双缝间距d,根据公式可知,条纹间的距离减小,B不符合要求;
C.增大双缝屏到光屏的距离L,根据公式可知,条纹间的距离增大,C符合要求;
D.根据公式可知,条纹间的距离与单缝屏到双缝屏的距离无关,D不符合要求。
故选C。
4.C
【解析】
实验中用激光通过双缝,双缝的作用是形成相干光源;由干涉条纹间距
知为了增大光屏上干涉条纹的间距,应使得双缝间距离d缩小,或者增大L与λ;
A.将光屏移近双缝,则L减小,不符合要求,故A错误;
B.增大双缝的间距d,导致条纹间距变小,故B错误;
C.换滤光片,改用频率更小即波长更长的单色光,符合要求,故C正确;
D.光源向双缝移动一小段距离,不会影响条纹间距,故D错误。
故选C。
5.C
【解析】
A.已知,由几何关系知入射角,折射角 ,则玻璃的折射率为
光在玻璃中传播速度
A错误;
B.发生全反射的临界角
因为
B错误;
CD.因为光线BN恰好在N点发生全反射,球心到光线BN的距离为
D错误C正确。
故选C。
6.C
【解析】
AC.由题分析可知,b光在I区域边缘发生了全反射,a光Ⅱ区域边缘发生了全反射,则知a光的临界角比b光的临界角大,由知,水对a光的折射率小于对b光的折射率,由折射定律知:a、b光从I区域某点倾斜射出时,a光折射角小,故A正确,不符合题意,C错误,符合题意;
B.水对a光的折射率小于对b光的折射率,则a光的频率小于b光的频率,由c=λf知,在真空中,因光速c不变,则有a光的波长大于b光的波长。故B正确,不符合题意;
D.水下a、b光经水面反射后均能射到图中I区域以外区域,故D正确,不符合题意。
故选C。
7.C
【解析】
单色光由空气射入玻璃砖时,折射角小于入射角。图甲错误。图乙正确;当该单色光由玻璃砖射入空气时,发生全反射的临界角的正弦值
因为
所以临界角,图丙、图丁中该单色光由玻璃砖射入空气时的入射角为,大于临界角,会发生全反射,图丙正确,图丁错误。
故选C。
8.D
【解析】
ABCD.由题,点波源S发出的电磁波经一负折射率平板介质后,折射光线与入射光线在法线的同一侧,所以不可能是光学1或2;根据光线穿过两侧平行的介质后的特点:方向与开始时的方向相同,所以光线3出介质右侧后,根据折射光线与入射光线在法线同侧这一条件,光线将无法汇聚形成实像;光线4才能满足“同侧”+“成实像”的条件,所以折射光线4可能是正确的,光线3是错误的,由以上的分析可知,ABC错误D正确。
故选D。
9.AC
【解析】
A.如图所示,作两界面法线相交于D点,在AB界面,由几何知识知,入射角为,折射角为,所以
故A正确;
B.光在BC界面上人射角为,则
即临界角
则在BC面上不会发生全反射,故B错误;
C.分析知BC面上折射角为,入射光线与出射光线相交于G点,,,则
,,
则
所以从F点出射的光束与入射到E点的光束的夹角为,故C正确;
D.紫光频率比红光频率大,棱镜对紫光的折射率大,若改用紫光沿相同角度从E点人射,则出射点在F点右侧,D错误。
故选AC。
10.ABD
【解析】
由图可知,单色光a偏折程度小于b的偏折程度,根据折射定律知,a光的折射率小于b光的折射率,则知a光的波长大.根据双缝干涉条纹的间距公式,可得,干涉条纹间距与波长成正比,所以a光的干涉条纹间距大于b光的干涉条纹间距,故A正确;a光的波长长,波动性强,更容易发生衍射现象,故B正确;由知,在水中a光的速度大,故C错误;由全反射临界角公式,知折射率n越大,临界角C越小,则知在水中a光的临界角大于b光的临界角,故D正确;若a光与b光以相同入射角从水射向空气时,由于在水中a光的临界角大于b光的临界角,所以b光的入射角先达到临界角,则b光先发生全反射,首先消失的是b光,故E错误.
11.ABD
【解析】
A.玻璃砖的折射率为
故A正确;
B.由折射定律得
可得
因此入射点与出射点之间的距离为
故B正确;
C.设临界角为,则有
可得
故C错误;
D.为了使从点以各种角度入射的光线都能从顶面射出,反射光线不能在顶面发生全反射,则底面反光膜至少为
故D正确;
故选ABD。
12.AD
【解析】
AB.由题图乙知,当时发生全反射,则有:
故选项A符合题意,B不符合题意;
C.图甲中若减小入射角,根据反射定律和折射定律可知反射角和折射角都减小,则反射光线和折射光线之间的夹角也将变大,故选项C不符合题意;
D.激光不从光导纤维束侧面外泄的临界条件是入射光在外侧面处发生全反射,临界光路如图所示,可得:
解得:,所以该束激光不从光导纤维束侧面外泄,则弯成的半圆形半径与纤维束半径应满足的关系为,故选项D符合题意。
13. 0.15 宽
【解析】游标卡尺的主尺读数为0mm,游标读数为0.05×3=0.15mm,所以最终读数为:0mm+0.15mm=0.15mm,根据条纹间距公式,可知当减小狭缝的宽度减小时,条纹间距变宽.
14.1.5 2.0×108
【解析】
(1)玻璃砖的折射率为
(2)光在玻璃中的传播速度
15.①60o② 60°
【解析】
①如图所示,在AB面发生折射,折射角r=30°,
由光的折射定律
则
i=60°
②因折射光线与底边BC平行,由光路可逆知第二次在AC面折射时的入射角为30°,折射角为60°,由几何关系可知
θ=2(i-30°)=60°
16.(1);(2)1m
【解析】
(1)据折射定律得
得
(2)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到G的距离d就是所求宽度。
设紫光临界角为,由全反射的知识得
得
中
得
中
得
17.(1);(2)。
【解析】
(1)光在透明体内的最长路径为2R,不考虑光在球内的反射,则有
透明体材料的折射率
;
(2)该光线的传播路径如图,入射角i=45°,折射率为n=,根据折射定律,则折射角r=30°
光从B点射出时的出射角为45°,由几何关系知,∠BOC=15°,∠BCO=30°,∠CBO=135°,由正弦定理,有
解得以45°的入射角射到A点的光,通过透明体后与O1O2的交点到球心O的距离
。
18.(i)(ii)
【解析】
(i)光从光源S射出经半球体到达水平桌面的光路如图
光由空气射向半球体,由折射定律,有
①
得
光束射出透明半球体,设入射角为,出射角设为,有
②
由几何关系有
③
联立②③得
由几何关系可知
④
得:
(ii)光在半球体中传播的速度为
⑤
得
由几何关系可知,为等腰三角形,光在透明半球体中传播的距离
⑥
得
该光束在透明半球体内传播的时间t
⑦
得
同课章节目录
- 第一章机械振动
- 1.1研究简谐运动
- 1.2探究物体做简谐运动的原因
- 1.3探究摆钟的物理原理
- 1.4探究单摆振动的周期
- 1.5受迫振动与共振
- 第二章机械波
- 2.1 机械波的产生
- 2.2 机械波的描述
- 2.3机械波的案例分析
- 2.4惠更斯原理 波的反射与折射
- 2.5波的干涉与衍射
- 2.6多普勒效应
- 第三章电磁场与电磁波
- 3.1麦克斯韦的电磁场理论
- 3.2电磁波的发现
- 3.3无线电通信
- 3.4电磁波家族
- 第四章光的波动性
- 4.1光的干涉
- 4.2用双缝干涉仪测定光的波长
- 4.3光的衍射
- 4.4光的偏振与立体电影
- 4.5光的折射
- 4.6全反射与光导纤维
- 4.7激光
- 第五章新时空观的确立
- 5.1电磁场理论引发的怪异问题
- 5.2狭义相对论的基本原理
- 5.3奇特的相对论效应
- 5.4走近广义相对论
- 5.5无穷的宇宙
