沪科版九年级数学上册 第23章《 解直角三角形》单元测试(含答案)
文档属性
| 名称 | 沪科版九年级数学上册 第23章《 解直角三角形》单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 439.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 13:07:15 | ||
图片预览



文档简介
第23章
解直角三角形
一、选择题
1.在Rt△ABC中,已知cosB=
,
则tanB的值为( )
A.????????????????B.?????????????C.?????????????????????????D.?
2.α是锐角,且sinα>
,
则α( )
A.?小于30°?????????????????????????????B.?大于30°?????????????????????????????C.?小于60°?????????????????????????????D.?大于60°
3.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=(??
)
A.??
???????????????????????????????????????B.??
???????????????????????????????????????C.??
???????????????????????????????????????D.??
4.如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是(??)
?
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.??
5.在△ABC中,若|sinA﹣|+(﹣tanB)2=0,则∠C的度数为( )
A.?30°??????????????????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????????????D.?120°
6.在Rt△ABC中,∠C=90°,AB=4,S△ABC=
,
则tanA+tanB=( )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?4
7.满足下列条件的△ABC
,
不是直角三角形的是( )
A.?∠C=∠A+∠B???????????B.?a:b:c=3:4:5???????????C.?∠C=∠A-∠B???????????D.?∠A:∠B:∠C=3:4:5
8.如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.?()米?????????????B.?()米???????????C.?()米??????????????D.?()米
9.已知在Rt△ABC中,∠C=90°,∠A=,BC=m,那么AB的长为(????)
A.?;???????????????????????????B.?;???????????????????????????C.?;???????????????????????????D.?.
10.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
11.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得AC=50米,则小岛B到公路l的距离为(???)米
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
12.若斜坡的坡比为1:
,则斜坡的坡角等于( )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
二、填空题
13.用不等号“>”或“<”连接:sin50°________?cos50°.
14.如图,Rt△ABC中,∠C=90°,BC=15,tanA=
,则AB=________.
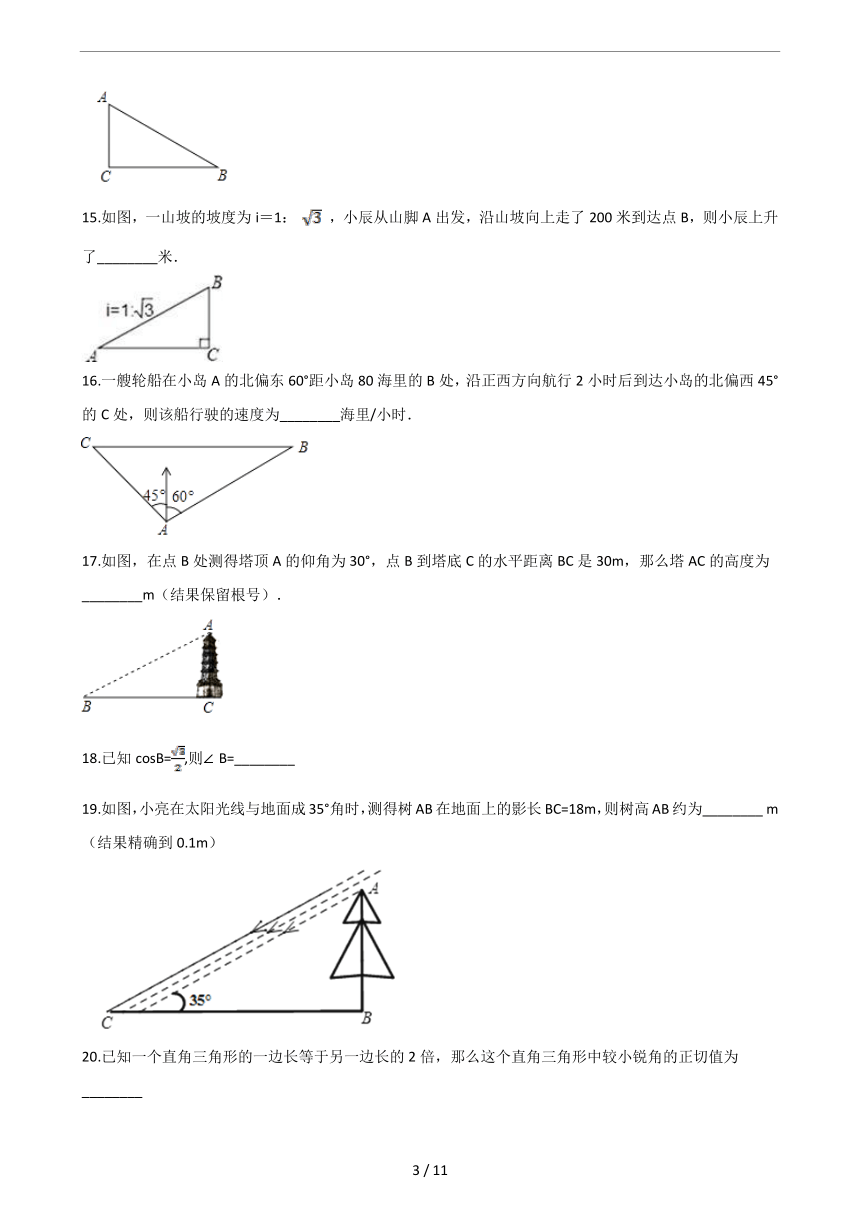
15.如图,一山坡的坡度为i=1:
,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了________米.
16.一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为________海里/小时.
17.如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为________m(结果保留根号).
18.已知cosB=,则∠B=________?
19.如图,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC=18m,则树高AB约为________?m(结果精确到0.1m)
?
20.已知一个直角三角形的一边长等于另一边长的2倍,那么这个直角三角形中较小锐角的正切值为________?
21.如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,则甲建筑物的高度为________?m,乙建筑物的高度为________?m.
22.请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个正n边形(n>4)的内角和是外角和的3倍,则n=________;
B.小明站在教学楼前50米处,测得教学楼顶部的仰角为20°,测角仪的高度为1.5米,则此教学楼的高度为________米.(用科学计算器计算,结果精确到0.1米)
三、解答题
23.某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:
≈1.41,
≈1.73,60千米/时=
米/秒)
24.如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
25.如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.
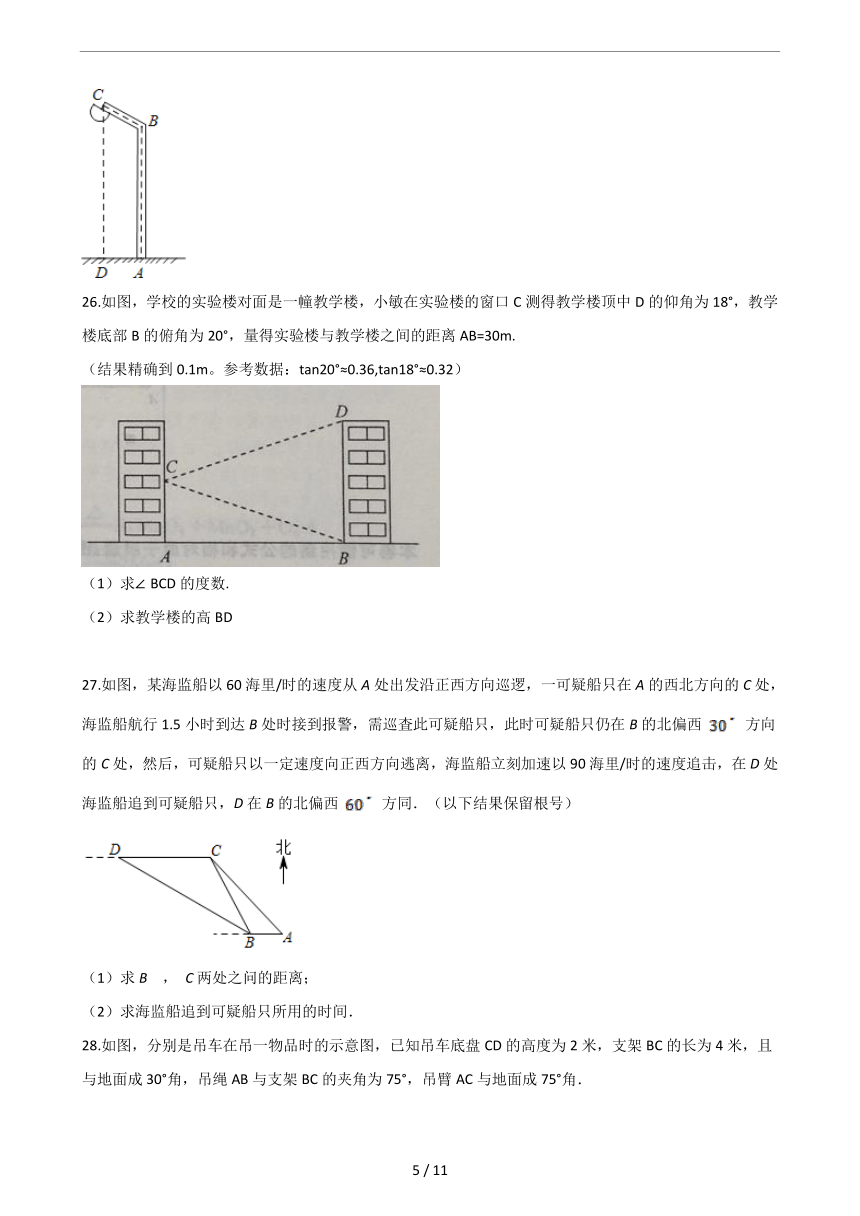
26.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶中D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)
(1)求∠BCD的度数.
(2)求教学楼的高BD
27.如图,某海监船以60海里/时的速度从A处出发沿正西方向巡逻,一可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西
方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西
方同.(以下结果保留根号)
(1)求B
,
C两处之问的距离;
(2)求海监船追到可疑船只所用的时间.
28.如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角.
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
参考答案
一、选择题
1.D
2.
D
3.
D
4.
A
5.
D
6.
C
7.
D
8.D
9.
C
10.A
11.B
12.
D
二、填空题
13.>
14.17
15.
100
16.20+20
17.
18.
30°
19.
12.6
20.,
21.30
;
22.8;19.7
三、解答题
23.解:过点P作PC⊥AB于点C.
在Rt△APC中,tan∠PAC=
,
∴AC=
=50
≈86.5(米),
同理,BC=
=PC=50(米),
∴AB=AC+BC≈136.5(米),
60千米/时=
米/秒,
则136.5÷
≈8.2>8.1.
故这辆车通过AB段超速.
24.
解:作DH⊥BC于H.设AE=x.
∵DH:BH=1:3,
在Rt△BDH中,DH2+(3DH)2=6002
,
∴DH=60
,BH=180
,
在Rt△ADE中,∵∠ADE=45°,
∴DE=AE=x,
∵又HC=ED,EC=DH,
∴HC=x,EC=60
,
在Rt△ABC中,tan33°=
,
∴x=
,
∴AC=AE+EC=
+60
=
.
答:山顶A到地面BC的高度AC是
米
25.
解:过B作BE⊥DC于E,设AB=x米,
∴CE=5.5﹣x,BC=6﹣x,
∵∠ABC=120°,
∴∠CBE=30°,
∴sin30°=,
解得:x=5,
答:AB的长度为5米.
?
26.(1)解:过点C作CD⊥BD于点E,
则∠DCE=18°,∠BCE=20°,
所以∠BCD=∠DCE+∠BCE=18°+20°=38°.
(2)解:由已知得CE=AB=30(m),
在Rt△CBE中,BE=CE×tan20°≈30×0.36=10.80(m),
在Rt△CDE中,DE=CE×tan18°≈30×0.32=9.60(m),
∴教学楼的高BD=BE+DE=10.80+9.60≈20.4(m).
答:教学楼的高为20.4m.
27.
(1)解:作
于E
,
如图1所示:则
,
由题意得:
(海里),
,
,
,
∴
是等腰直角三角形,
,
∴
,
,
∴
,
,
设
,则
,
,
∴
,
解得:
,
∴
;
答:B
,
C两处之问的距离为
海里
(2)解:作
于F
,
如图2所示:
则
,
,
∴
,
∴海监船追到可疑船只所用的时间为
(小时);
答:海监船追到可疑船只所用的时间为
小时.
28.(1)证明:如图,∵∠BCH=30°,∠ACE=75°,
∴∠ACB=180°﹣∠BCH﹣∠ACE=75°,
∵∠ABC=75°,
∴∠ABC=∠BCA,
∴AB=AC
(2)解:作AL⊥BC于L,在AE上截取一点M,使得AM=MC.
在△ACL和△ACE中,
,
∴△ACL≌△ACE,
∴CL=CE,
∵AB=AC,AL⊥BC,BC=4,
∴BL=CL=CE=2,
∵MA=MC,
∴∠MAC=∠MCA=90°﹣∠ACE=15°,
∴∠CME=30°,
∴CM=AM=2CE=4,ME=2
,
∴AE=AM+ME=4+2
,
∴AF=AE+EF=4+2
+2=6+2
.
吊车的吊臂顶端A点距地面的高度是(6+2
)米.
PAGE
/
NUMPAGES
解直角三角形
一、选择题
1.在Rt△ABC中,已知cosB=
,
则tanB的值为( )
A.????????????????B.?????????????C.?????????????????????????D.?
2.α是锐角,且sinα>
,
则α( )
A.?小于30°?????????????????????????????B.?大于30°?????????????????????????????C.?小于60°?????????????????????????????D.?大于60°
3.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=(??
)
A.??
???????????????????????????????????????B.??
???????????????????????????????????????C.??
???????????????????????????????????????D.??
4.如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是(??)
?
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.??
5.在△ABC中,若|sinA﹣|+(﹣tanB)2=0,则∠C的度数为( )
A.?30°??????????????????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????????????D.?120°
6.在Rt△ABC中,∠C=90°,AB=4,S△ABC=
,
则tanA+tanB=( )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?4
7.满足下列条件的△ABC
,
不是直角三角形的是( )
A.?∠C=∠A+∠B???????????B.?a:b:c=3:4:5???????????C.?∠C=∠A-∠B???????????D.?∠A:∠B:∠C=3:4:5
8.如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.?()米?????????????B.?()米???????????C.?()米??????????????D.?()米
9.已知在Rt△ABC中,∠C=90°,∠A=,BC=m,那么AB的长为(????)
A.?;???????????????????????????B.?;???????????????????????????C.?;???????????????????????????D.?.
10.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
11.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得AC=50米,则小岛B到公路l的距离为(???)米
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
12.若斜坡的坡比为1:
,则斜坡的坡角等于( )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
二、填空题
13.用不等号“>”或“<”连接:sin50°________?cos50°.
14.如图,Rt△ABC中,∠C=90°,BC=15,tanA=
,则AB=________.
15.如图,一山坡的坡度为i=1:
,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了________米.
16.一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为________海里/小时.
17.如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为________m(结果保留根号).
18.已知cosB=,则∠B=________?
19.如图,小亮在太阳光线与地面成35°角时,测得树AB在地面上的影长BC=18m,则树高AB约为________?m(结果精确到0.1m)
?
20.已知一个直角三角形的一边长等于另一边长的2倍,那么这个直角三角形中较小锐角的正切值为________?
21.如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,则甲建筑物的高度为________?m,乙建筑物的高度为________?m.
22.请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个正n边形(n>4)的内角和是外角和的3倍,则n=________;
B.小明站在教学楼前50米处,测得教学楼顶部的仰角为20°,测角仪的高度为1.5米,则此教学楼的高度为________米.(用科学计算器计算,结果精确到0.1米)
三、解答题
23.某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:
≈1.41,
≈1.73,60千米/时=
米/秒)
24.如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
25.如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.
26.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶中D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)
(1)求∠BCD的度数.
(2)求教学楼的高BD
27.如图,某海监船以60海里/时的速度从A处出发沿正西方向巡逻,一可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西
方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西
方同.(以下结果保留根号)
(1)求B
,
C两处之问的距离;
(2)求海监船追到可疑船只所用的时间.
28.如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角.
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
参考答案
一、选择题
1.D
2.
D
3.
D
4.
A
5.
D
6.
C
7.
D
8.D
9.
C
10.A
11.B
12.
D
二、填空题
13.>
14.17
15.
100
16.20+20
17.
18.
30°
19.
12.6
20.,
21.30
;
22.8;19.7
三、解答题
23.解:过点P作PC⊥AB于点C.
在Rt△APC中,tan∠PAC=
,
∴AC=
=50
≈86.5(米),
同理,BC=
=PC=50(米),
∴AB=AC+BC≈136.5(米),
60千米/时=
米/秒,
则136.5÷
≈8.2>8.1.
故这辆车通过AB段超速.
24.
解:作DH⊥BC于H.设AE=x.
∵DH:BH=1:3,
在Rt△BDH中,DH2+(3DH)2=6002
,
∴DH=60
,BH=180
,
在Rt△ADE中,∵∠ADE=45°,
∴DE=AE=x,
∵又HC=ED,EC=DH,
∴HC=x,EC=60
,
在Rt△ABC中,tan33°=
,
∴x=
,
∴AC=AE+EC=
+60
=
.
答:山顶A到地面BC的高度AC是
米
25.
解:过B作BE⊥DC于E,设AB=x米,
∴CE=5.5﹣x,BC=6﹣x,
∵∠ABC=120°,
∴∠CBE=30°,
∴sin30°=,
解得:x=5,
答:AB的长度为5米.
?
26.(1)解:过点C作CD⊥BD于点E,
则∠DCE=18°,∠BCE=20°,
所以∠BCD=∠DCE+∠BCE=18°+20°=38°.
(2)解:由已知得CE=AB=30(m),
在Rt△CBE中,BE=CE×tan20°≈30×0.36=10.80(m),
在Rt△CDE中,DE=CE×tan18°≈30×0.32=9.60(m),
∴教学楼的高BD=BE+DE=10.80+9.60≈20.4(m).
答:教学楼的高为20.4m.
27.
(1)解:作
于E
,
如图1所示:则
,
由题意得:
(海里),
,
,
,
∴
是等腰直角三角形,
,
∴
,
,
∴
,
,
设
,则
,
,
∴
,
解得:
,
∴
;
答:B
,
C两处之问的距离为
海里
(2)解:作
于F
,
如图2所示:
则
,
,
∴
,
∴海监船追到可疑船只所用的时间为
(小时);
答:海监船追到可疑船只所用的时间为
小时.
28.(1)证明:如图,∵∠BCH=30°,∠ACE=75°,
∴∠ACB=180°﹣∠BCH﹣∠ACE=75°,
∵∠ABC=75°,
∴∠ABC=∠BCA,
∴AB=AC
(2)解:作AL⊥BC于L,在AE上截取一点M,使得AM=MC.
在△ACL和△ACE中,
,
∴△ACL≌△ACE,
∴CL=CE,
∵AB=AC,AL⊥BC,BC=4,
∴BL=CL=CE=2,
∵MA=MC,
∴∠MAC=∠MCA=90°﹣∠ACE=15°,
∴∠CME=30°,
∴CM=AM=2CE=4,ME=2
,
∴AE=AM+ME=4+2
,
∴AF=AE+EF=4+2
+2=6+2
.
吊车的吊臂顶端A点距地面的高度是(6+2
)米.
PAGE
/
NUMPAGES
