人教版数学八年级上册14.1.4 整式的乘法 第2课时 课件(14张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.1.4 整式的乘法 第2课时 课件(14张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第2课时
14.1.4
整式的乘法
计算:1.单项式乘以单项式
2.单项式乘以多项式
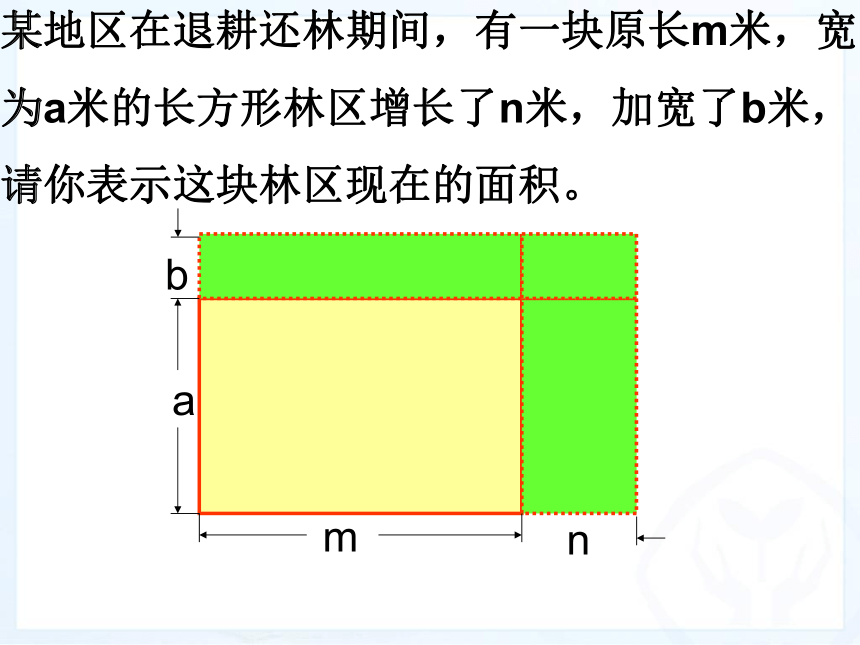
某地区在退耕还林期间,有一块原长m米,宽
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。
ma
na
mb
nb
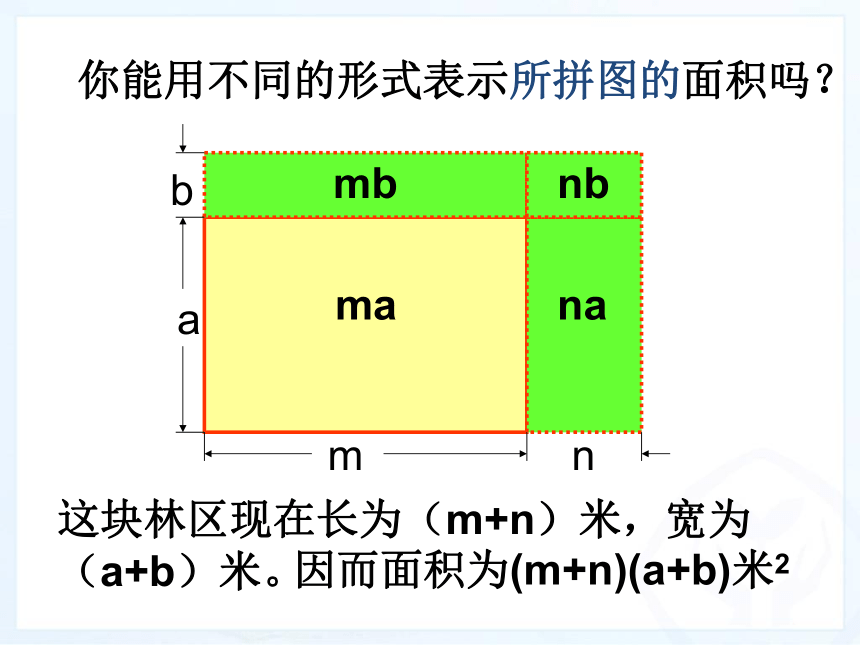
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米。
因而面积为(m+n)(a+b)米2
如何证明
(a+b)(m+n)=am+an+bm+bn
呢?
左边=
(a+b)(m+n)
把m+n看成X
=(a+b)X
=aX+bX
=a(m+n)+b(m+n)
=am+an+bm+bn
=右边
用m+n换回X
(a+b)(m+n)
=
am
1
2
3
4
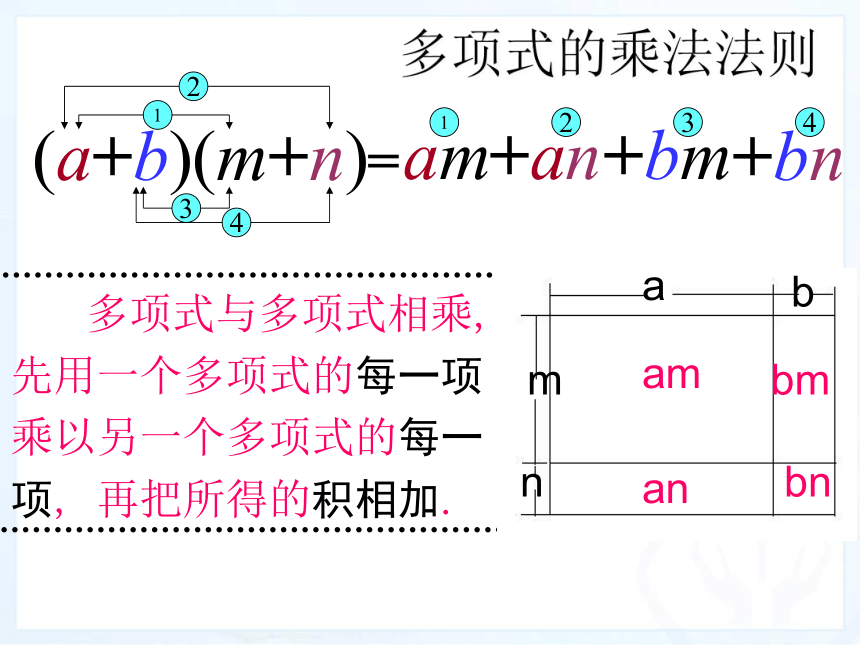
多项式的乘法法则
+an
+bm
+bn
多项式与多项式相乘,
先用一个多项式的每一项乘以另一个多项式的每一项,
再把所得的积相加.
a
b
m
n
am
an
bn
bm
例题解析
【例4】计算:
(1)(x+2)(x?3),
(2)(3x
-1)(2x+1)。
-3x
+2x
=
x2
-x-6
-2×3
(2)
(3x
-1)(2x+1)
=
3x?2x
+3x?
1
-1?2
x
-1
=
6x2
+3x
-2
x
-1
=
6x2
+x-1.
1.计算
(1)
(2x+1)(x+3);
(2)
(m+2n)(m+
3n):
(3)
(
a
-
1)2
;
(4)
(a+3b)(a
–3b
).
(5)
(x+2)(x+3);
(6)
(x-4)(x+1)
(7)
(y+4)(y-2);
(8)
(y-5)(y-3)
答案:(1)
2x2+7x+3;
(2)
m2+5mn+6n2;
(3)
a2-2a+1;
(4)
a2-9b2
(5)
x2+5x+6;
(6)
x2-3x-4;
(7)
y2+2y-8;
(8)
y2-8y+15.
x
p+q
pq
新知巩固
根据上述求解过程,观察计算结果的各项系数与原
式中的系数有怎样的关系?
根据上述结论计算:
(1)
(x+1)(x+2)=
(2)
(x+1)(x-2)=
(3)
(x-1)(x+2)=
(4)
(x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q)
=
x2
+
(p+q)
x
+
p
q
拓展与应用
1.(a+
b)
(m
+n)=
am+
bm+
an+
bn
2.(a+
b+c)
(m
+n)=
am+an+bm+bn+cm+cn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
3.(x+p)(x+q)
=
x2
+
(p+q)
x
+
p
q
先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2
综合应用(例)
若m,n是整数,且有
(mx-3y)(3x+2y)=6x2-nxy-6y2
求m,n的值
解:
(mx-3y)(3x+2y)
=3mx2+2mxy-9xy-6y2
=
3mx2+(2m-9)
xy-6y2
比较系数得:
3m=6
2m-9=-n
解得:
m=2
n=5
第2课时
14.1.4
整式的乘法
计算:1.单项式乘以单项式
2.单项式乘以多项式
某地区在退耕还林期间,有一块原长m米,宽
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。
ma
na
mb
nb
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米。
因而面积为(m+n)(a+b)米2
如何证明
(a+b)(m+n)=am+an+bm+bn
呢?
左边=
(a+b)(m+n)
把m+n看成X
=(a+b)X
=aX+bX
=a(m+n)+b(m+n)
=am+an+bm+bn
=右边
用m+n换回X
(a+b)(m+n)
=
am
1
2
3
4
多项式的乘法法则
+an
+bm
+bn
多项式与多项式相乘,
先用一个多项式的每一项乘以另一个多项式的每一项,
再把所得的积相加.
a
b
m
n
am
an
bn
bm
例题解析
【例4】计算:
(1)(x+2)(x?3),
(2)(3x
-1)(2x+1)。
-3x
+2x
=
x2
-x-6
-2×3
(2)
(3x
-1)(2x+1)
=
3x?2x
+3x?
1
-1?2
x
-1
=
6x2
+3x
-2
x
-1
=
6x2
+x-1.
1.计算
(1)
(2x+1)(x+3);
(2)
(m+2n)(m+
3n):
(3)
(
a
-
1)2
;
(4)
(a+3b)(a
–3b
).
(5)
(x+2)(x+3);
(6)
(x-4)(x+1)
(7)
(y+4)(y-2);
(8)
(y-5)(y-3)
答案:(1)
2x2+7x+3;
(2)
m2+5mn+6n2;
(3)
a2-2a+1;
(4)
a2-9b2
(5)
x2+5x+6;
(6)
x2-3x-4;
(7)
y2+2y-8;
(8)
y2-8y+15.
x
p+q
pq
新知巩固
根据上述求解过程,观察计算结果的各项系数与原
式中的系数有怎样的关系?
根据上述结论计算:
(1)
(x+1)(x+2)=
(2)
(x+1)(x-2)=
(3)
(x-1)(x+2)=
(4)
(x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q)
=
x2
+
(p+q)
x
+
p
q
拓展与应用
1.(a+
b)
(m
+n)=
am+
bm+
an+
bn
2.(a+
b+c)
(m
+n)=
am+an+bm+bn+cm+cn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
3.(x+p)(x+q)
=
x2
+
(p+q)
x
+
p
q
先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2
综合应用(例)
若m,n是整数,且有
(mx-3y)(3x+2y)=6x2-nxy-6y2
求m,n的值
解:
(mx-3y)(3x+2y)
=3mx2+2mxy-9xy-6y2
=
3mx2+(2m-9)
xy-6y2
比较系数得:
3m=6
2m-9=-n
解得:
m=2
n=5
