相似三角形复习学案

相似三角形复习学案
一、知识解读：
1、两个三角形相似的条件。具体为：
a ）两角 的两个三角形相似；b ）三边 的两个三角形相似；c ）两边 且夹角 的两个三角形相似。
2、两个相似三角形的性质。具体为：
a ）相似三角形的对应角 ；b ）相似三角形的对应边 ；
c ）相似三角形的对应角平分线、中线、高线的比等于 ；
d ）相似三角形的周长的比等于 。e）相似三角形的面积的比等于 。
3、常见三角形相似的基本图形、基本条件和基本结论：
3.1平行线截三角形二边相似：
基本条件：DE∥BC 基本结论：△ADE∽△ABC；每个图形中有一对相似三角形。
特例：
基本条件：DE⊥AC，BC⊥AC
基本结论：△ADE∽△ACB；图形中有一对相似三角形。
3.2直线斜截三角形二边相似：
基本条件：∠ADE=∠ACB，或∠AED=∠ABC，
或AE：AB=AD：AC
基本结论：△ADE∽△ACB；图形中有一对相似三角形
特例：
基本条件：∠BDE=∠BAC，或BD：AB=BE：BC
或DE：AC=BE：BC
基本结论：△BDE∽△BAC；图形中有一对相似三角形
3.3过三角形一顶点斜截三角形一边相似：
基本条件：∠ADE=∠ACB，或∠ACD=∠ABC，或AC：AB=AD：AC
基本结论：△ADC∽△ACB；图形中有一对相似三角形
特例： 基本条件：∠BCA=∠CDB=90°，
基本结论：△BDC∽△BCA；△ADC∽△ABC；
△BDC∽△CDA；图形中有三对相似三角形。
4、相似多边形
（1）定义：（只能用定义判定两个多边形相似）：
可总结为三个条件；① ② ③
(2)相似多边形的性质: ①相似多边形的对应边 ，对应角 .
②相似多边形的周长之比都等于 ③相似多边形面积之比等于 .
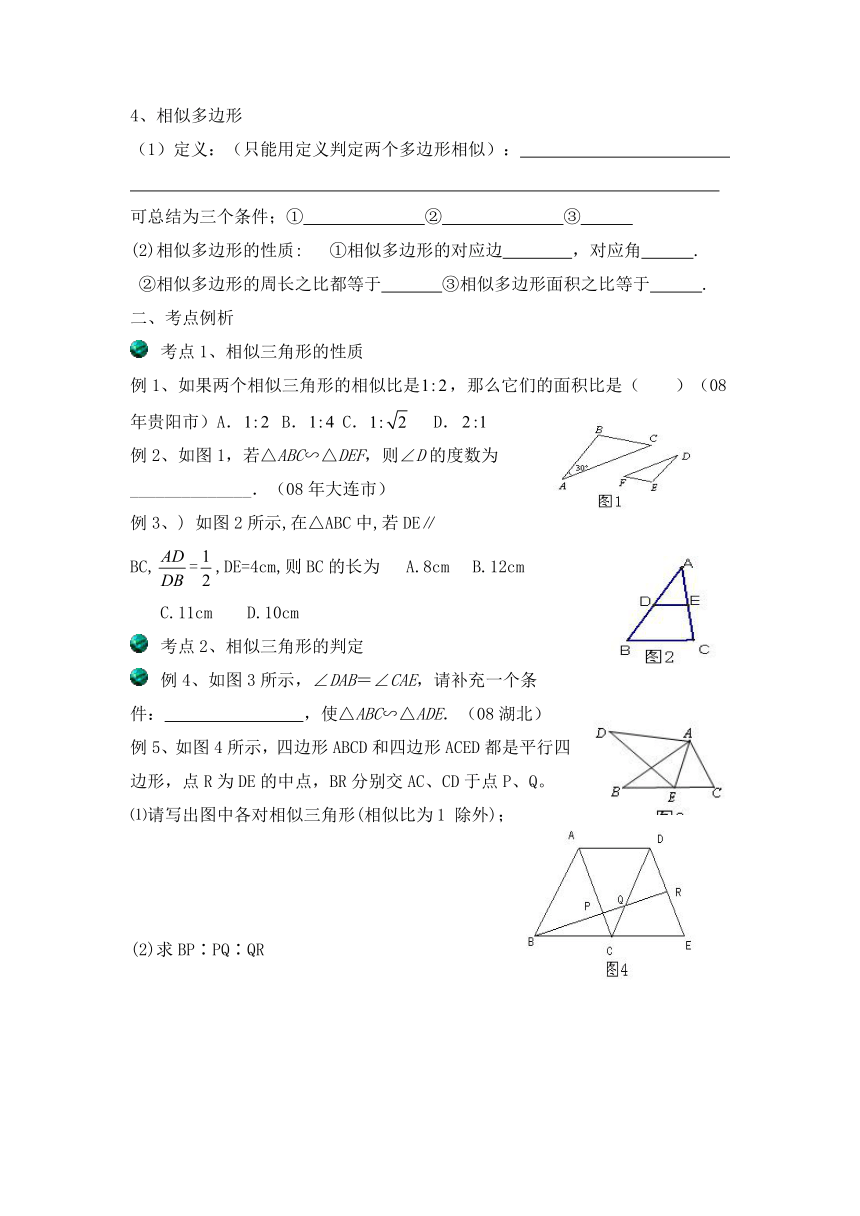
二、考点例析
考点1、相似三角形的性质
例1、如果两个相似三角形的相似比是，那么它们的面积比是（ ）（08年贵阳市）A． B． C． D．
例2、如图1，若△ABC∽△DEF，则∠D的度数为______________．（08年大连市）
例3、) 如图2所示,在△ABC中,若DE∥BC,=,DE=4cm,则BC的长为 A.8cm B.12cm C.11cm D.10cm
考点2、相似三角形的判定
例4、如图3所示，∠DAB＝∠CAE，请补充一个条件： ，使△ABC∽△ADE．（08湖北）
例5、如图4所示，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR分别交AC、CD于点P、Q。
⑴请写出图中各对相似三角形(相似比为1 除外)；
(2)求BP∶PQ∶QR
考点3、相似三角形的实际应用
例6、阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺、标杆、一副三角尺、小平面镜。请你在他们提供的测量工具中选出所需工具，设计一种测量方案。
（1）所需的测量工具是： ；
（2）请在图5中画出测量示意图；
（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x.
考点4、相似多边形的性质
例7.（1）两个相似的五边形，一组对应边的长分别是3厘米和4.5厘米，如果它们的面积之和是78厘米2，则较大的五边形的面积是________厘米2.
(2)把一个矩形剪去一个正方形，所剩矩形与原矩形相似，则原矩形的长边与短边的比值等于________.
三、巩固和提高
1．填空：
（1）如果两个相似三角形对应边的比为1∶2 ，那么它们的相似比为________，周长的比为_____，面积的比为_____．
（2）如果两个相似三角形面积的比为1∶2 ，那么它们的相似比为________，周长的比为________．
（3）连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______，面积比等于_______．
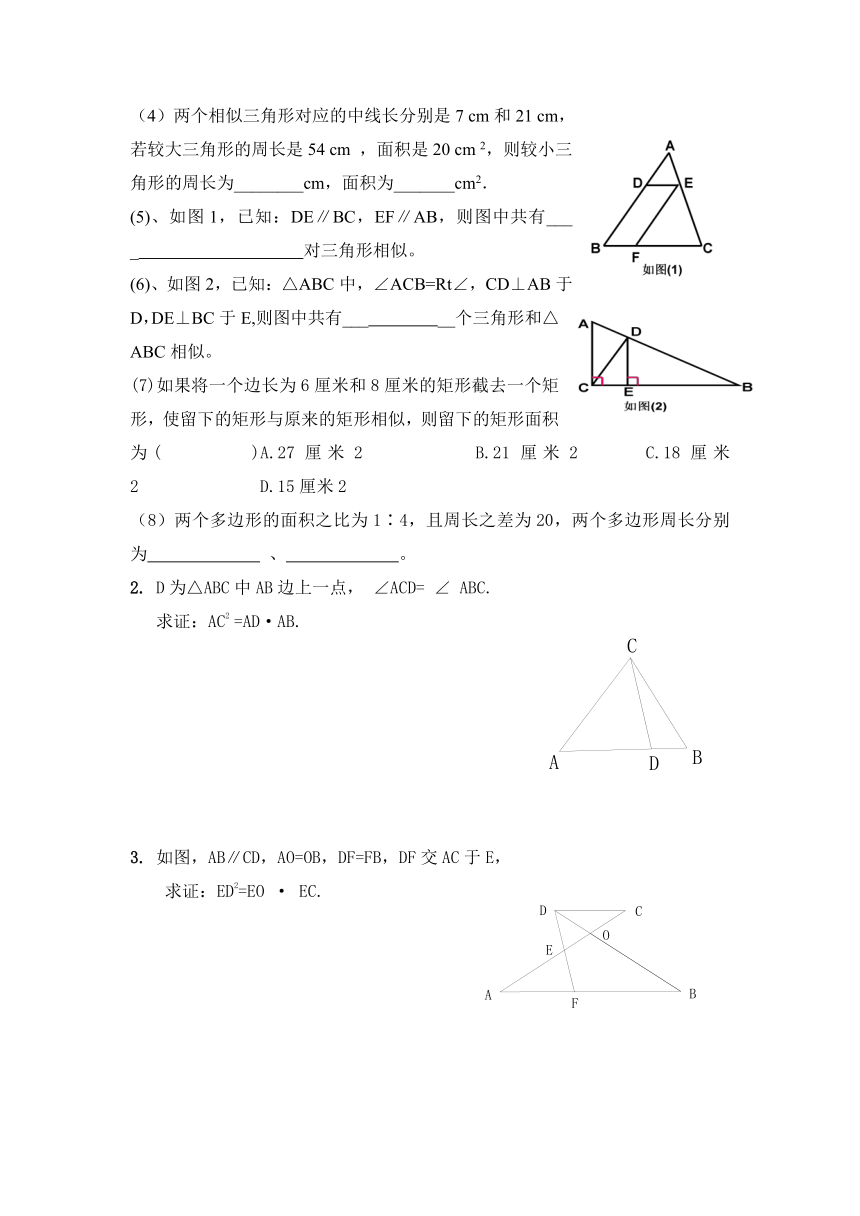
（4）两个相似三角形对应的中线长分别是7 cm和21 cm，若较大三角形的周长是54 cm ，面积是20 cm 2，则较小三角形的周长为________cm，面积为_______cm2．
(5)、如图1，已知：DE∥BC，EF∥AB，则图中共有___ _ 对三角形相似。
(6)、如图2，已知：△ABC中，∠ACB=Rt∠，CD⊥AB于D，DE⊥BC于E,则图中共有___ __个三角形和△ABC相似。
(7)如果将一个边长为6厘米和8厘米的矩形截去一个矩形，使留下的矩形与原来的矩形相似，则留下的矩形面积为( )A.27厘米2 B.21厘米2 C.18厘米2 D.15厘米2
（8）两个多边形的面积之比为1∶4，且周长之差为20，两个多边形周长分别为 、 。
2. D为△ABC中AB边上一点， ∠ACD= ∠ ABC.
求证：AC2 =AD·AB.
3. 如图，AB∥CD，AO=OB，DF=FB，DF交AC于E，
求证：ED2=EO · EC.
3.过◇ABCD的一个顶点A作一直线分别交对角线BD、边 BC、边DC的延长线于E、F、G . 求证：EA2 = EF· EG .
4. 已知在△ABC中，∠BAC=90°，AD⊥BC，E是AC的 中点，ED交AB的延长线于F. 求证: AB:AC=DF:AF.
5、如图，已知：△ABC中，DE∥AC，EF∥AB，S四边形ADEF =S三角形ABC，BC=5。求BE之长。
5、在△ABC中，AB=AC=8，∠A=36，BD平分∠ABC。求AD之长。
条件探索型
1.已知：如图，△ABC中，P是AB边上的一点，连结CP．满足什么条件时
△ ACP∽△ABC．
2.如图：已知∠ABC＝∠CDB＝90°，AC＝a，BC=b，当BD与a、b之间满足怎样的关系式时，两三角形相似
2、结论探索型
1.将两块完全相同的等腰直角三角板摆成如图的样子，假设图形中的所有点、线都在同一平面内，则图中有相似（不包括全等）三角形吗？如有，把它们一 一写出来.
2.△在ABC中，AB>AC，过AB上一点D作直线DE交另一边于E，使所得三角形与原三角形相似，画出满足条件的图形
存在探索型
如图, DE是△ABC的中位线，∠B=90° ，AF ∥BC，在射线AF上是否存在点M，使△MEC与△ADE相似,若存在,请先确定点 M,再证明这两个三角形相似，若不存在，请说明理由.
实际应用题：1、甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为 ________米．
2、小强用这样的方法来测量学校教学楼的高度：如图，在地面上放一面镜子（镜子高度忽略不计），他刚好能从镜子中看到教学楼的顶端B，他请同学协助量了镜子与教学楼的距离EA=21米，以及他与镜子的距离CE=2.5米，已知他的眼睛距离地面的高度DC=1.6米，请你帮助小强计算出教学楼的高度。（根据光的反射定律：反射角等于入射角）
1.两相似三角形的周长之比是1：4，那么它们的对应边上的高之比是（ ）
A：1：2 B： 4：1 C：2：1 D：1：4
2.如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△ABC～△ADE的是（ ）
A. B.
C.∠B=∠D D ∠C=∠AED
3、已知：DE∥BC，AD：BD=1：2，
①则?△ADE与?△ABC面积之比是 ；
②?△ADE与四边形DECB的面积之比是
例题：已知△ABC中，DE∥BC，AD=3DB，S△ABC=48，求S四边形BDEC
如图，点D、E分别是△ABC边AB、AC上的点，
且DE∥BC，BD＝2AD，那么△ADE的周长︰△ABC的周长＝　　　　．
1、.在平行四边形ABCD中，点E为CD的中点，连AE并延长与BC的延长线交于点F，若S△CEF =10，求四边形ABCE的面积
例2.如图，在已建立直角坐标系的4×4正方形方格纸中，画出符号条件的格点三角形（三角形的三个顶点都是小正方形的顶点），若以格点P，A，B为顶点的三角形与△ABC相似（全等除外），则格点P的坐标是_______．
拓展变式 在Rt△ABC中，斜边AC上有一动点D（不与点A，C重合），过D点作直线截△ABC，使截得的三角形与△ABC相似，则满足这样条件的直线共有______条．
例3. 如图，已知平行四边形ABCD中，E是AB边的中点，DE交AC于点F，下面结论：①只有一对相似三角形；②EF：ED=1：2；③AF：FC=1：2；．其中正确的结论是（ ）
A．①③ B．③ C．① D．①②
拓展变式 点G是□ABCD的边BC延长线上的一点，AG与BD相交于点E，与CD相交于点F，则图中相似三角形共有（ ）
A．3对 B．4对 C．5对 D．6对
例4.如图，已知在ΔABC中，AB=BC，BD⊥AC于点D，CE⊥AB于点E，BD与CE交于点H．
（1）写出所有与ΔDHC相似的三角形；
（2）求证：DA2=DH·DB．
A
P
B
C
1
2
3
A
B
C
a
b
D
D
A
B
C
A
B
D
E
G
F
１
2
A
D
B
C
E
F
甲
小华乙
甲
小华乙
B
C
E
A
D
2
1
友情提示：要求面积比，就要先求出相似比
友情提示：
思路点拨：（1）可先说明△ ∽△
（2）再求出AD：AB=
（3）再求S△ADE：S△ABC=
从而求得S△ADE
（4）最后求得S四边形BDEC
A
E
D
C
B
F
E
D
C
B
A
C
A
B
D
E
F
H
E
D
C
B
A