华东师大版九年级数学下册 27.2.3切线-切线长定理课件(共21张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册 27.2.3切线-切线长定理课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 926.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 16:26:17 | ||
图片预览






文档简介
(共21张PPT)
27.2.3.2切线长定理
目标引领
1、知识与技能
1.了解切线长定理的探究与演绎推理,会运用切线长定理进行计算和证明.
2.知道三角形的内切圆和内心以及圆的外切三角形的意义.
2、过程与方法
1.在探究切线长定理的过程中,培养学生的动手操作能力和演绎归纳能力.
2.在运用切线长定理进行证明的过程中感受几何推理的严谨性,培养学生的逻辑推理能力.
3、情感、态度与价值观
1.通在探究分析切线长定理,感受数学知识形成的严谨性,培养学生良好的学习习惯.
2.在自主探究中体会成功的快乐,增强学好数学的信心,在分组交流中培养协作意识.
温故知新
1.什么是圆的切线?圆的切线有什么性质?
2.怎样判断一条直线是圆的切线?
3.过圆外一点画圆的切线,可以画几条?
预习导航
1.自己任意画一个圆,并在圆外任意取一点,过这点画圆的两条切线,测量到切点的线段长度,对比分析测量结果.
2.结合教材52页学习切线长的意义.
3.结合1中的测量对比,并运用轴对称的性质分析总结切线长定理:
4运用切线的性质定理结合全等三角形的知识演技证明切线长定理.
5.结合教材54页,分析探究在三角形内截取最大圆的问题.
6.学习三角形的内切圆、内心和圆的外切三角形的概念.
·
在经过圆外一点的切线上,这一点和切点之间的
线段的长叫做这点到圆的切线长
O
P
A
思考:
切线和切线长这两个概念有何区别?
·
O
P
A
B
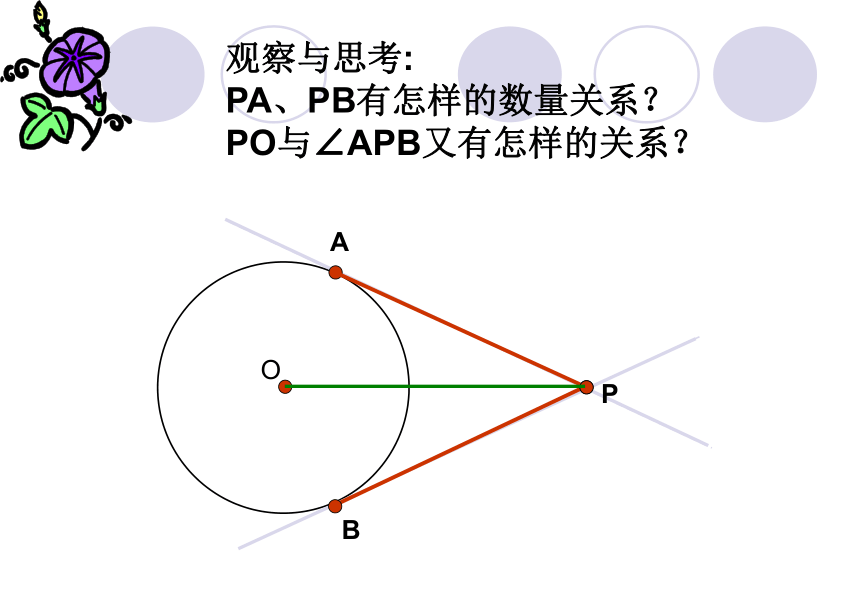
观察与思考:
PA、PB有怎样的数量关系?
PO与∠APB又有怎样的关系?
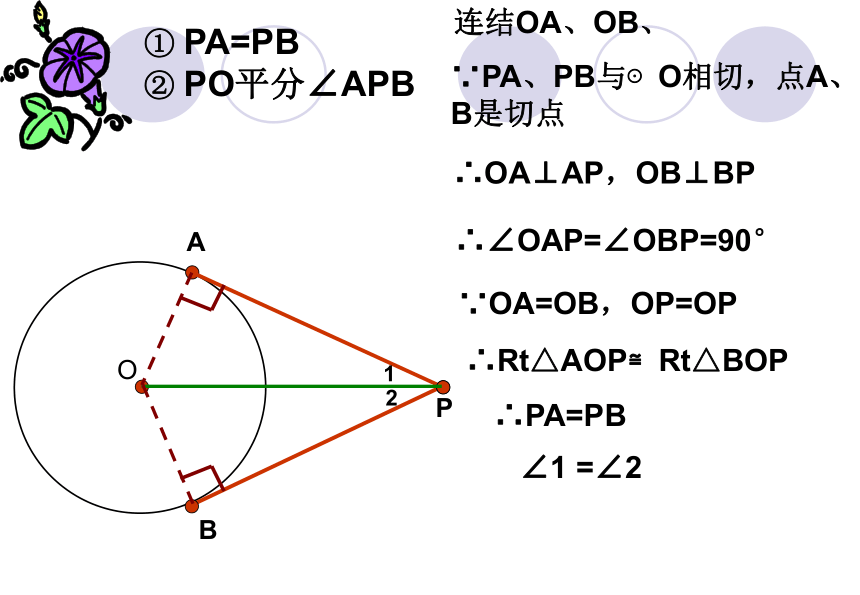
∴Rt△AOP≌Rt△BOP
·
O
P
A
B
①
PA=PB
②
PO平分∠APB
1
2
连结OA、OB、
∵PA、PB与⊙O相切,点A、B是切点
∠1
=∠2
∴OA⊥AP,OB⊥BP
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
∴PA=PB
切线长定理
从圆外一点可以引圆的两条切线,
它们的切线长相等,
这一点和圆心的连线平分两条切线的夹角。
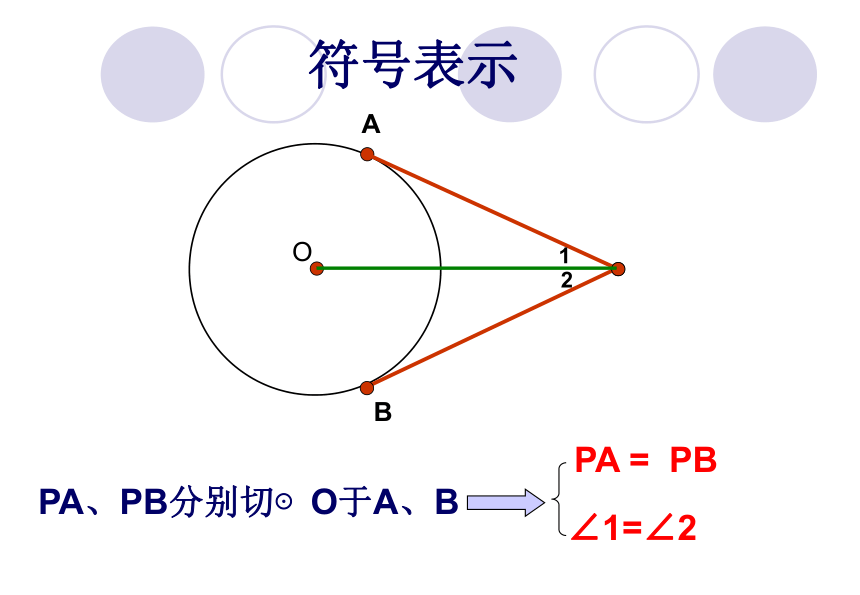
PA、PB分别切⊙O于A、B
PA
=
PB
∠1=∠2
·
O
A
B
1
2
符号表示
(1)写出图中所有的垂直关系
OA⊥PA,OB
⊥PB,AB
⊥OP
(3)写出图中所有的全等三角形
△AOP≌
△BOP,
△AOC≌
△BOC,
△ACP≌
△BCP
(4)写出图中所有的等腰三角形
△ABP,
△AOB
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
。
P
B
A
O
反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
问题:已知:P为⊙O外一点,PA、PB为⊙O的切线,
A、B为切点,BC是直径。
求证:AC∥OP
D
A
B
C
思考:
如图是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
问题:如图△ABC,要求画△ABC的内切圆,如何画?
已知:△ABC
求作:和△ABC的各边都相切的圆
B
C
A
I
D
作法:1、作∠B、∠C的平分线BM、CN,交点为I
2、过点I作ID⊥BC,垂足为D
3、以I为圆心,ID为半径作⊙I
⊙I就是所求的圆
N
M
┐
与三角形各边都相切的圆
叫做三角形的内切圆
A
B
C
I
┐
┐
D
E
F
三角形内切圆的圆心叫做三角形的内心
这个三角形叫做圆的外切三角形
三角形的内心就是三角形的三个内角角平分线的交点
三角形的内心到三角形的三边的距离相等
小试锋芒:
如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A
、B,在AB上任取一点C作⊙O的切线分别交PA
、PB于D
、E
(1)若PA=2,则△PDE的周长为____;若PA=a,则△PDE的周长为_____。
(2)连结OD
、OE,若∠P=40
°,则∠DOE=_____;
若∠P=k,∠DOE=___________
度
。
E
O
C
B
D
P
A
4
2a
70
°
知识梳理
1、归纳小结:
(1)切线长定理:
(2)三角形的内切圆、内心和圆的外切三角形的概念:
2、方法规律:
(1)过圆外一点作圆的两条切线:该点与圆心、切点所成的四边形的对角互补.
(2)三角形的内切圆半径为r,三角形周长为c,面积为S:则有S=cr
学以致用
1.
如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5B.7C.8D.10
2.
如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于
.
3.如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
畅谈收获
27.2.3.2切线长定理
目标引领
1、知识与技能
1.了解切线长定理的探究与演绎推理,会运用切线长定理进行计算和证明.
2.知道三角形的内切圆和内心以及圆的外切三角形的意义.
2、过程与方法
1.在探究切线长定理的过程中,培养学生的动手操作能力和演绎归纳能力.
2.在运用切线长定理进行证明的过程中感受几何推理的严谨性,培养学生的逻辑推理能力.
3、情感、态度与价值观
1.通在探究分析切线长定理,感受数学知识形成的严谨性,培养学生良好的学习习惯.
2.在自主探究中体会成功的快乐,增强学好数学的信心,在分组交流中培养协作意识.
温故知新
1.什么是圆的切线?圆的切线有什么性质?
2.怎样判断一条直线是圆的切线?
3.过圆外一点画圆的切线,可以画几条?
预习导航
1.自己任意画一个圆,并在圆外任意取一点,过这点画圆的两条切线,测量到切点的线段长度,对比分析测量结果.
2.结合教材52页学习切线长的意义.
3.结合1中的测量对比,并运用轴对称的性质分析总结切线长定理:
4运用切线的性质定理结合全等三角形的知识演技证明切线长定理.
5.结合教材54页,分析探究在三角形内截取最大圆的问题.
6.学习三角形的内切圆、内心和圆的外切三角形的概念.
·
在经过圆外一点的切线上,这一点和切点之间的
线段的长叫做这点到圆的切线长
O
P
A
思考:
切线和切线长这两个概念有何区别?
·
O
P
A
B
观察与思考:
PA、PB有怎样的数量关系?
PO与∠APB又有怎样的关系?
∴Rt△AOP≌Rt△BOP
·
O
P
A
B
①
PA=PB
②
PO平分∠APB
1
2
连结OA、OB、
∵PA、PB与⊙O相切,点A、B是切点
∠1
=∠2
∴OA⊥AP,OB⊥BP
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
∴PA=PB
切线长定理
从圆外一点可以引圆的两条切线,
它们的切线长相等,
这一点和圆心的连线平分两条切线的夹角。
PA、PB分别切⊙O于A、B
PA
=
PB
∠1=∠2
·
O
A
B
1
2
符号表示
(1)写出图中所有的垂直关系
OA⊥PA,OB
⊥PB,AB
⊥OP
(3)写出图中所有的全等三角形
△AOP≌
△BOP,
△AOC≌
△BOC,
△ACP≌
△BCP
(4)写出图中所有的等腰三角形
△ABP,
△AOB
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
。
P
B
A
O
反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
问题:已知:P为⊙O外一点,PA、PB为⊙O的切线,
A、B为切点,BC是直径。
求证:AC∥OP
D
A
B
C
思考:
如图是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
问题:如图△ABC,要求画△ABC的内切圆,如何画?
已知:△ABC
求作:和△ABC的各边都相切的圆
B
C
A
I
D
作法:1、作∠B、∠C的平分线BM、CN,交点为I
2、过点I作ID⊥BC,垂足为D
3、以I为圆心,ID为半径作⊙I
⊙I就是所求的圆
N
M
┐
与三角形各边都相切的圆
叫做三角形的内切圆
A
B
C
I
┐
┐
D
E
F
三角形内切圆的圆心叫做三角形的内心
这个三角形叫做圆的外切三角形
三角形的内心就是三角形的三个内角角平分线的交点
三角形的内心到三角形的三边的距离相等
小试锋芒:
如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A
、B,在AB上任取一点C作⊙O的切线分别交PA
、PB于D
、E
(1)若PA=2,则△PDE的周长为____;若PA=a,则△PDE的周长为_____。
(2)连结OD
、OE,若∠P=40
°,则∠DOE=_____;
若∠P=k,∠DOE=___________
度
。
E
O
C
B
D
P
A
4
2a
70
°
知识梳理
1、归纳小结:
(1)切线长定理:
(2)三角形的内切圆、内心和圆的外切三角形的概念:
2、方法规律:
(1)过圆外一点作圆的两条切线:该点与圆心、切点所成的四边形的对角互补.
(2)三角形的内切圆半径为r,三角形周长为c,面积为S:则有S=cr
学以致用
1.
如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5B.7C.8D.10
2.
如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于
.
3.如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
畅谈收获
