华东师大版九年级数学下册 26.2.3 求二次函数的表达式 课件(共18张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册 26.2.3 求二次函数的表达式 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 629.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
求二次函数的表达式
同学们,加
油啊!
二次函数是初中代数的重要内容之一,也是历年中考的重点。这部分知识命题形式比较灵活,既有填空题、选择题,又有解答题,而且常与方程、几何、三角形等综合在一起,出现在压轴题之中。
因此,熟练掌握二次函数的相关知识,会灵活运用一般式、顶点式、交点式求二次函数的表达式是解决综合应用题的基础和关键。
一、二次函数常用的几种表达式的确定
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标或对称轴,选择交点式。
1、一般式
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标,
可将原函数用顶点式表示,再根据“左加右减,上加下减“的法则,即可得出所求新函数的表达式。
二、求二次函数表达式的思想方法
1、
求二次函数表达式的常用方法:
2、求二次函数表达式的
常用思想:
3、二次函数表达式的最终形式:
待定系数法、配方法、数形结合等。
转化思想
解方程或方程组
无论采用哪一种表达式求解,最后结果都化为一般式。
例1、已知二次函数
的图像如图所示,
求其表达式。
解法一:
一般式
设表达式为
∵顶点C(1,4),
∴对称轴
x=1.
∵A(-1,0)关于
x=1对称,
∴B(3,0)。
∵A(-1,0)、B(3,0)和
C(1,4)在抛物线上,
∴
即:
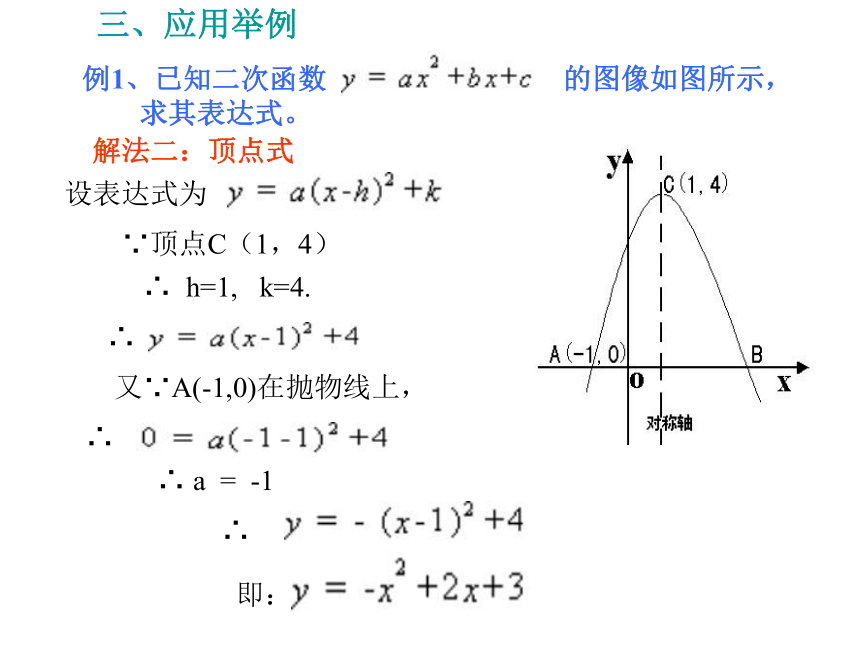
三、应用举例
例1、已知二次函数
的图像如图所示,
求其表达式。
解法二:顶点式
设表达式为
∵顶点C(1,4)
∴
又∵A(-1,0)在抛物线上,
∴
∴
a
=
-1
即:
∴
∴
h=1,
k=4.
三、应用举例
解法三:交点式
设表达式为
∵抛物线与x
轴的两个交点坐标
为
A
(-1,0)、B(3,0)
∴
y
=
a
(x+1)
(x-
3)
又
C(1,4)在抛物线上
∴
4
=
a
(1+1)
(1-3)
∴
a
=
-1
∴
y
=
-
(
x+1)
(x-3)
即:
例1、已知二次函数
的图像如图所示,
求其表达式。
三、应用举例
评析:
本题可采用一般式、顶点式和交点式求解,通过对比可发现用顶点式和交点式求解比用一般式求解简便。同时也培养学生一题多思、一题多解的能力,从不同角度进行思维开放、解题方法开放的培养。注重解题技巧的养成训练,可事半功倍。
近年中考数学命题趋势,贴近学生生活,联系实际,把实际问题转化为数学模型,培养学生分析问题、解决问题的能力,增强学以致用的意识。
例2、已知:如图,是某一抛物线形拱形桥,拱桥底面宽度OB是12米,当水位是2米时,测得水面宽度AC是8米。
(1)求拱桥所在抛物线的表达式;
(2)当水位是2.5米时,高1.4米的船能否通过拱桥?请说明理由(不考虑船的宽度。船的高度指船在水面上的高度)。
三、应用举例
即:
∴
E
F
a
=
-0.1
解:(1)、由图可知:四边形ACBO是等腰梯形
过A、C作OB的垂线,垂足为E、F点。
∴
OE
=
BF
=(12-8)÷2
=
2。
∴O(0,0),B(-12,0),A(-2,2)。
设解析式为
又
∵A(-2,2)点在图像上,
三、应用举例
例2、已知:如图,是某一抛物线形拱形桥,拱桥底面宽度OB是12米,当水位是2米时,测得水面宽度AC是8米。
(1)求拱桥所在抛物线的表达式;
(2)当水位是2.5米时,高1.4米的船能否通过拱桥?请说明理由(不考虑船的宽度。船的高度指船在水面上的高度)。
P
Q
(2)、分析:船能否通过,只要看船在拱桥正中间时,船及水位的高度是否超过拱桥顶点的纵坐标。
y
=
水位+船高
=2.5+1.4
=3.9
>
3.6
解:
∵
∴
∴顶点(-6,3.6),
当水位为2.5米时,
∴
船不能通过拱桥。
PQ是对称轴。
复习二次函数四种平移关系
例3、将抛物线
向左平移4个单位长度,再向下平移3个单位长度,求平移后所得抛物线的表达式。
解法:将二次函数的表达式
转化为顶点式得:
(1)、由
向左平移4个单位得:
(左加右减)
(2)、再将
向下平移3个单位得
(上加下减)
即:所求的表达式为
三、应用举例
1、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其表达式。
∴
四、尝试练习
解:设二次函数的表达式为
∵
x
=
1,
y=
-1
,
∴顶点(1,-1)。
又(0,0)在抛物线上,
∴
a
=
1
即:
∴
∴
2、已知二次函数与x
轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其表达式。
解:设所求的表达式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴
a
=
-1
即:
∴
∴
∴
四、尝试练习
3、如图;有一个抛物线形的隧道桥拱,这个桥拱的最大高度为3.6m,跨度为7.2m.一辆卡车车高3米,宽1.6米,它能否通过隧道?
四、尝试练习
即当x=
OC=1.6÷2=0.8米时,过C点作CD⊥AB交抛物线于D点,若y=CD≥3米,则卡车可以通过。
分析:卡车能否通过,只要看卡车在隧道正中间时,其车高3米是否超过其位置的拱高。
四、尝试练习
4、将二次函数
的图像向右平移1个单位,
再向上平移4个单位,求其表达式。
解:∵
二次函数表达式为
(1)、由
向右平移1个单位得:
(左加右减)
(2)、再把
向上平移4个单位得:
(上加下减)
即:所求的表达式为
五、小结
1、二次函数常用表达式
.已知图象上三点坐标,通常选择一般式。
.已知图象的顶点坐标(对称轴或最值),通常选择顶点式。
.已知图象与x轴的两个交点的横坐标x1、x2,
通常选择交点式。
3.
确定二次函数的解析式的关键是根据条件的特点,恰当地选择一种函数表达式,灵活应用。
一般式
顶点式
交点式
2、求二次函数表达式的一般方法:
已知图象中发生变化的只有顶点坐标,通常选择平移式。
平移式
不能降低对自己的要求,因为你还能做得更好!
老师的希望:
求二次函数的表达式
同学们,加
油啊!
二次函数是初中代数的重要内容之一,也是历年中考的重点。这部分知识命题形式比较灵活,既有填空题、选择题,又有解答题,而且常与方程、几何、三角形等综合在一起,出现在压轴题之中。
因此,熟练掌握二次函数的相关知识,会灵活运用一般式、顶点式、交点式求二次函数的表达式是解决综合应用题的基础和关键。
一、二次函数常用的几种表达式的确定
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标或对称轴,选择交点式。
1、一般式
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标,
可将原函数用顶点式表示,再根据“左加右减,上加下减“的法则,即可得出所求新函数的表达式。
二、求二次函数表达式的思想方法
1、
求二次函数表达式的常用方法:
2、求二次函数表达式的
常用思想:
3、二次函数表达式的最终形式:
待定系数法、配方法、数形结合等。
转化思想
解方程或方程组
无论采用哪一种表达式求解,最后结果都化为一般式。
例1、已知二次函数
的图像如图所示,
求其表达式。
解法一:
一般式
设表达式为
∵顶点C(1,4),
∴对称轴
x=1.
∵A(-1,0)关于
x=1对称,
∴B(3,0)。
∵A(-1,0)、B(3,0)和
C(1,4)在抛物线上,
∴
即:
三、应用举例
例1、已知二次函数
的图像如图所示,
求其表达式。
解法二:顶点式
设表达式为
∵顶点C(1,4)
∴
又∵A(-1,0)在抛物线上,
∴
∴
a
=
-1
即:
∴
∴
h=1,
k=4.
三、应用举例
解法三:交点式
设表达式为
∵抛物线与x
轴的两个交点坐标
为
A
(-1,0)、B(3,0)
∴
y
=
a
(x+1)
(x-
3)
又
C(1,4)在抛物线上
∴
4
=
a
(1+1)
(1-3)
∴
a
=
-1
∴
y
=
-
(
x+1)
(x-3)
即:
例1、已知二次函数
的图像如图所示,
求其表达式。
三、应用举例
评析:
本题可采用一般式、顶点式和交点式求解,通过对比可发现用顶点式和交点式求解比用一般式求解简便。同时也培养学生一题多思、一题多解的能力,从不同角度进行思维开放、解题方法开放的培养。注重解题技巧的养成训练,可事半功倍。
近年中考数学命题趋势,贴近学生生活,联系实际,把实际问题转化为数学模型,培养学生分析问题、解决问题的能力,增强学以致用的意识。
例2、已知:如图,是某一抛物线形拱形桥,拱桥底面宽度OB是12米,当水位是2米时,测得水面宽度AC是8米。
(1)求拱桥所在抛物线的表达式;
(2)当水位是2.5米时,高1.4米的船能否通过拱桥?请说明理由(不考虑船的宽度。船的高度指船在水面上的高度)。
三、应用举例
即:
∴
E
F
a
=
-0.1
解:(1)、由图可知:四边形ACBO是等腰梯形
过A、C作OB的垂线,垂足为E、F点。
∴
OE
=
BF
=(12-8)÷2
=
2。
∴O(0,0),B(-12,0),A(-2,2)。
设解析式为
又
∵A(-2,2)点在图像上,
三、应用举例
例2、已知:如图,是某一抛物线形拱形桥,拱桥底面宽度OB是12米,当水位是2米时,测得水面宽度AC是8米。
(1)求拱桥所在抛物线的表达式;
(2)当水位是2.5米时,高1.4米的船能否通过拱桥?请说明理由(不考虑船的宽度。船的高度指船在水面上的高度)。
P
Q
(2)、分析:船能否通过,只要看船在拱桥正中间时,船及水位的高度是否超过拱桥顶点的纵坐标。
y
=
水位+船高
=2.5+1.4
=3.9
>
3.6
解:
∵
∴
∴顶点(-6,3.6),
当水位为2.5米时,
∴
船不能通过拱桥。
PQ是对称轴。
复习二次函数四种平移关系
例3、将抛物线
向左平移4个单位长度,再向下平移3个单位长度,求平移后所得抛物线的表达式。
解法:将二次函数的表达式
转化为顶点式得:
(1)、由
向左平移4个单位得:
(左加右减)
(2)、再将
向下平移3个单位得
(上加下减)
即:所求的表达式为
三、应用举例
1、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其表达式。
∴
四、尝试练习
解:设二次函数的表达式为
∵
x
=
1,
y=
-1
,
∴顶点(1,-1)。
又(0,0)在抛物线上,
∴
a
=
1
即:
∴
∴
2、已知二次函数与x
轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其表达式。
解:设所求的表达式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴
a
=
-1
即:
∴
∴
∴
四、尝试练习
3、如图;有一个抛物线形的隧道桥拱,这个桥拱的最大高度为3.6m,跨度为7.2m.一辆卡车车高3米,宽1.6米,它能否通过隧道?
四、尝试练习
即当x=
OC=1.6÷2=0.8米时,过C点作CD⊥AB交抛物线于D点,若y=CD≥3米,则卡车可以通过。
分析:卡车能否通过,只要看卡车在隧道正中间时,其车高3米是否超过其位置的拱高。
四、尝试练习
4、将二次函数
的图像向右平移1个单位,
再向上平移4个单位,求其表达式。
解:∵
二次函数表达式为
(1)、由
向右平移1个单位得:
(左加右减)
(2)、再把
向上平移4个单位得:
(上加下减)
即:所求的表达式为
五、小结
1、二次函数常用表达式
.已知图象上三点坐标,通常选择一般式。
.已知图象的顶点坐标(对称轴或最值),通常选择顶点式。
.已知图象与x轴的两个交点的横坐标x1、x2,
通常选择交点式。
3.
确定二次函数的解析式的关键是根据条件的特点,恰当地选择一种函数表达式,灵活应用。
一般式
顶点式
交点式
2、求二次函数表达式的一般方法:
已知图象中发生变化的只有顶点坐标,通常选择平移式。
平移式
不能降低对自己的要求,因为你还能做得更好!
老师的希望:
