人教版七年级下册数学课件9.2.2实际问题与一元一次不等式 课件(共16张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件9.2.2实际问题与一元一次不等式 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 13:31:54 | ||
图片预览






文档简介
(共16张PPT)
9.2.2实际问题与一元一次不等式
一元一次一不等式的解法
解一元一次不等式,根据不等式的性质,将不等
式逐步化为
x
>a(或
x
<
a
)的形式,
一般步骤为:去分母、去括号、移项、合并、系
数化为
1(注意不等号的改变问题)
自学展示:
利用不等式解决实际问题
列不等式解应用题的基本步骤与列方
程解应用题步骤类似。
1、审
2、设
3、列
4、解
5、答
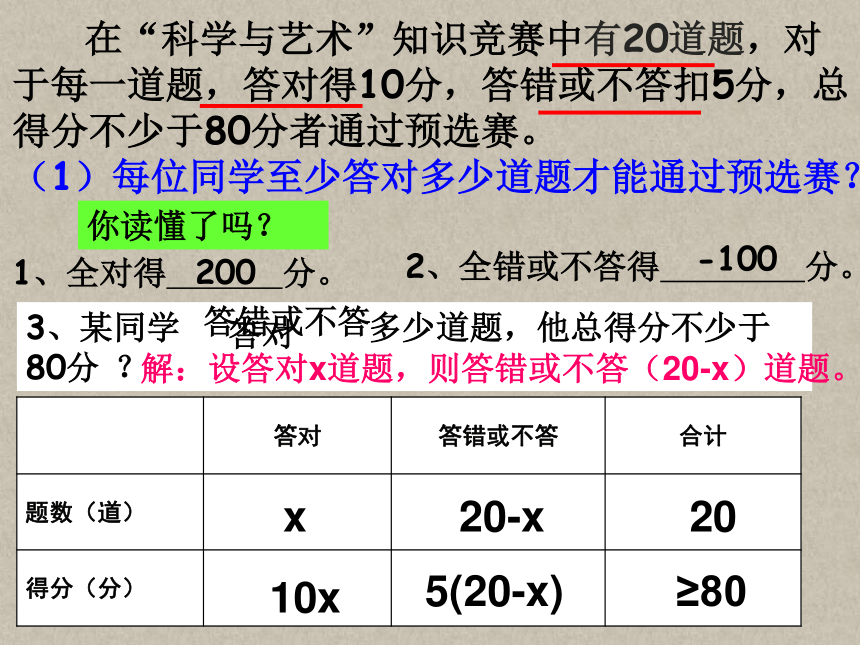
在“科学与艺术”知识竞赛中有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预选赛。
(1)每位同学至少答对多少道题才能通过预选赛?
你读懂了吗?
1、全对得
分。
3、某同学
多少道题,他总得分不少于80分
?
2、全错或不答得
分。
200
-100
答对
答错或不答
x
20-x
20
10x
5(20-x)
≥80
解:设答对x道题,则答错或不答(20-x)道题。
答对
答错或不答
合计
题数(道)
得分(分)
解:设答对x道题,则答错或不答(20-x)道题。
移项
:
10x
+
5x
≥
100
+
80
系数化为1:
x
≥
12
10x
-
5(20
-
x
)≥
80
去括号:
10x
-
100
+
5x
≥
80
合并同类型:
15x
≥
180
答:每位同学至少答对12道题才能通过预选赛。
甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费.顾客怎样选择商店购物能获得更大优惠?
合作学习:
分析:甲商店优惠方案的起点为购物款达___元后
100
50
乙商店优惠方案的起点为购物款达___元后.
我们是否应分情况考虑?可以怎样分情况呢?
x
x
x
50+0.95(x-50)
50+0.95(x-50)
100+0.9(x-100)
解:设累计购物
x
元。
购物款
x<50
50≤x<100
x
≥
100
甲店
乙店
(1)
若到甲商场购物花费少,则
50
+
0.95
(
x
-
50)
>
100
+
0.9(x
-
100
)
解得
x
>
150
当累计购物超过150元时,到甲商场花费少。
解:当累计购物超过100元时,设累计购物x(x
?100)元。
(2)若到乙商场购物花费少,则
50
+
0.95
(x
-
50)
<
100
+
0.9(x
-
100)
解得
x
<
150
当累计购物超过100元不到150元时,到乙商场花费少。
(3)若50
+
0.95
(
x
-
50)
=
100
+
0.9(x
-
100)
解得
x
=
150
当累计购物150元时,到甲乙商场的花费一样。
质疑导学:
某商店出售茶壶和茶杯,茶壶每只20元,茶杯每只5元,该商店有两种优惠办法:
(1)买一只茶壶送一只茶杯;
(2)按总价的92%付款.
现有一顾客需购买4只茶壶,茶杯若干只(不少于4只).请问:顾客买同样多的茶杯时,用哪一种优惠办法购买省钱?
解:设顾客买茶杯的个数为x(x≥4)个,则
1)方案一需付费用为4×20
+
5(x
-
4)=(5x
+
60)元
方案二需付费用为
92%(20×4
+
5x)=(4.6x
+
73.6)元
(2)①方案一省钱,5x+60<4.6x+73.6,解得x<34;
②方案二省钱,5x+60>4.6x+73.6,解得x>34;
③两种方案都一样,5x+60=4.6x+73.6,解得x=34;
答:当x<34时,方案一省钱;当x>34时,方案二省钱;当x=34,两种方案都一样.
1、
某校校长暑假将带领该校市级优秀学生乘旅行社的车去A市参加科技夏令营,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠”.乙旅行社说:“包括校长在内全部按全票的6折优惠”,若全票价为240元.
(1)设学生数为x,甲旅行社收费为y甲,乙旅行社收费为y乙.分别计算两家旅行社的收费(建立表达式);
(2)当学生数是多少时,两家旅行社的收费一样?
(3)
就学生数x讨论哪家旅行社更优惠.
学习检测
解:(1)
y甲=120x+240
y乙=144x+144
(2)
120x+240=144x+144
24x=96
x=4
(3)
?
120x+240>144x+144
x<4
∴当人数x小于4时,甲旅行社优惠。
?
120x+240<144x+144
x>4
∴当人数x大于4时,乙旅行社优惠。
?
120x+240=144x+144
x=4
∴当人数x等于4时,两家旅行社价格一样
答:(2)当人数x等于4时,两家旅行社价格一样。
(3)当人数x小于4时,甲旅行社优惠;
当人数x大于4时,乙旅行社优惠;
当人数x等于4时,两家旅行社价格一样。
2、某人的手机话费可选择两种收费办法中的一种,甲种收费办法是,先交月租15元,每通一分钟电话再收费0.10元;乙种收费办法是,不交月租费,每通一分钟电话收费0.20元.问每月通话时间在什么范围内选择甲种收费办法合适?在什么范围内时选择乙种收费办法合适?
解:设此人每个月的通话时间为x分钟(x≥0),则:
甲方案的收费总额:15+0.1x;乙方案的收费总额:0.2x;
若甲方案优惠,则:15+0.1x<0.2x,解得:x>150;
若乙方案优惠,那么:15+0.2x>0.2x,解得:0≤x<125;
若两种方案收费相同,那么:15+0.2x=0.2x,解得:x=150;
答:当每月通话时间少于分钟时,选乙方案合适;
若等于150分钟,两种方案的收费相同;
若通话时间超过150分钟,选甲方案更合适.
实际问题
课堂小结
应用一元一次不等式解实际问题步骤:
作业:习题1、2
9.2.2实际问题与一元一次不等式
一元一次一不等式的解法
解一元一次不等式,根据不等式的性质,将不等
式逐步化为
x
>a(或
x
<
a
)的形式,
一般步骤为:去分母、去括号、移项、合并、系
数化为
1(注意不等号的改变问题)
自学展示:
利用不等式解决实际问题
列不等式解应用题的基本步骤与列方
程解应用题步骤类似。
1、审
2、设
3、列
4、解
5、答
在“科学与艺术”知识竞赛中有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预选赛。
(1)每位同学至少答对多少道题才能通过预选赛?
你读懂了吗?
1、全对得
分。
3、某同学
多少道题,他总得分不少于80分
?
2、全错或不答得
分。
200
-100
答对
答错或不答
x
20-x
20
10x
5(20-x)
≥80
解:设答对x道题,则答错或不答(20-x)道题。
答对
答错或不答
合计
题数(道)
得分(分)
解:设答对x道题,则答错或不答(20-x)道题。
移项
:
10x
+
5x
≥
100
+
80
系数化为1:
x
≥
12
10x
-
5(20
-
x
)≥
80
去括号:
10x
-
100
+
5x
≥
80
合并同类型:
15x
≥
180
答:每位同学至少答对12道题才能通过预选赛。
甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费.顾客怎样选择商店购物能获得更大优惠?
合作学习:
分析:甲商店优惠方案的起点为购物款达___元后
100
50
乙商店优惠方案的起点为购物款达___元后.
我们是否应分情况考虑?可以怎样分情况呢?
x
x
x
50+0.95(x-50)
50+0.95(x-50)
100+0.9(x-100)
解:设累计购物
x
元。
购物款
x<50
50≤x<100
x
≥
100
甲店
乙店
(1)
若到甲商场购物花费少,则
50
+
0.95
(
x
-
50)
>
100
+
0.9(x
-
100
)
解得
x
>
150
当累计购物超过150元时,到甲商场花费少。
解:当累计购物超过100元时,设累计购物x(x
?100)元。
(2)若到乙商场购物花费少,则
50
+
0.95
(x
-
50)
<
100
+
0.9(x
-
100)
解得
x
<
150
当累计购物超过100元不到150元时,到乙商场花费少。
(3)若50
+
0.95
(
x
-
50)
=
100
+
0.9(x
-
100)
解得
x
=
150
当累计购物150元时,到甲乙商场的花费一样。
质疑导学:
某商店出售茶壶和茶杯,茶壶每只20元,茶杯每只5元,该商店有两种优惠办法:
(1)买一只茶壶送一只茶杯;
(2)按总价的92%付款.
现有一顾客需购买4只茶壶,茶杯若干只(不少于4只).请问:顾客买同样多的茶杯时,用哪一种优惠办法购买省钱?
解:设顾客买茶杯的个数为x(x≥4)个,则
1)方案一需付费用为4×20
+
5(x
-
4)=(5x
+
60)元
方案二需付费用为
92%(20×4
+
5x)=(4.6x
+
73.6)元
(2)①方案一省钱,5x+60<4.6x+73.6,解得x<34;
②方案二省钱,5x+60>4.6x+73.6,解得x>34;
③两种方案都一样,5x+60=4.6x+73.6,解得x=34;
答:当x<34时,方案一省钱;当x>34时,方案二省钱;当x=34,两种方案都一样.
1、
某校校长暑假将带领该校市级优秀学生乘旅行社的车去A市参加科技夏令营,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠”.乙旅行社说:“包括校长在内全部按全票的6折优惠”,若全票价为240元.
(1)设学生数为x,甲旅行社收费为y甲,乙旅行社收费为y乙.分别计算两家旅行社的收费(建立表达式);
(2)当学生数是多少时,两家旅行社的收费一样?
(3)
就学生数x讨论哪家旅行社更优惠.
学习检测
解:(1)
y甲=120x+240
y乙=144x+144
(2)
120x+240=144x+144
24x=96
x=4
(3)
?
120x+240>144x+144
x<4
∴当人数x小于4时,甲旅行社优惠。
?
120x+240<144x+144
x>4
∴当人数x大于4时,乙旅行社优惠。
?
120x+240=144x+144
x=4
∴当人数x等于4时,两家旅行社价格一样
答:(2)当人数x等于4时,两家旅行社价格一样。
(3)当人数x小于4时,甲旅行社优惠;
当人数x大于4时,乙旅行社优惠;
当人数x等于4时,两家旅行社价格一样。
2、某人的手机话费可选择两种收费办法中的一种,甲种收费办法是,先交月租15元,每通一分钟电话再收费0.10元;乙种收费办法是,不交月租费,每通一分钟电话收费0.20元.问每月通话时间在什么范围内选择甲种收费办法合适?在什么范围内时选择乙种收费办法合适?
解:设此人每个月的通话时间为x分钟(x≥0),则:
甲方案的收费总额:15+0.1x;乙方案的收费总额:0.2x;
若甲方案优惠,则:15+0.1x<0.2x,解得:x>150;
若乙方案优惠,那么:15+0.2x>0.2x,解得:0≤x<125;
若两种方案收费相同,那么:15+0.2x=0.2x,解得:x=150;
答:当每月通话时间少于分钟时,选乙方案合适;
若等于150分钟,两种方案的收费相同;
若通话时间超过150分钟,选甲方案更合适.
实际问题
课堂小结
应用一元一次不等式解实际问题步骤:
作业:习题1、2
