2019-2020学年湖南师大附中博才实验中学八年级下学期期中数学试卷 (含部分答案)
文档属性
| 名称 | 2019-2020学年湖南师大附中博才实验中学八年级下学期期中数学试卷 (含部分答案) |  | |
| 格式 | doc | ||
| 文件大小 | 379.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 06:52:58 | ||
图片预览


文档简介
2019-2020学年湖南师大附中博才实验中学八年级第二学期期中数学试卷
一.选择题(共12小题).
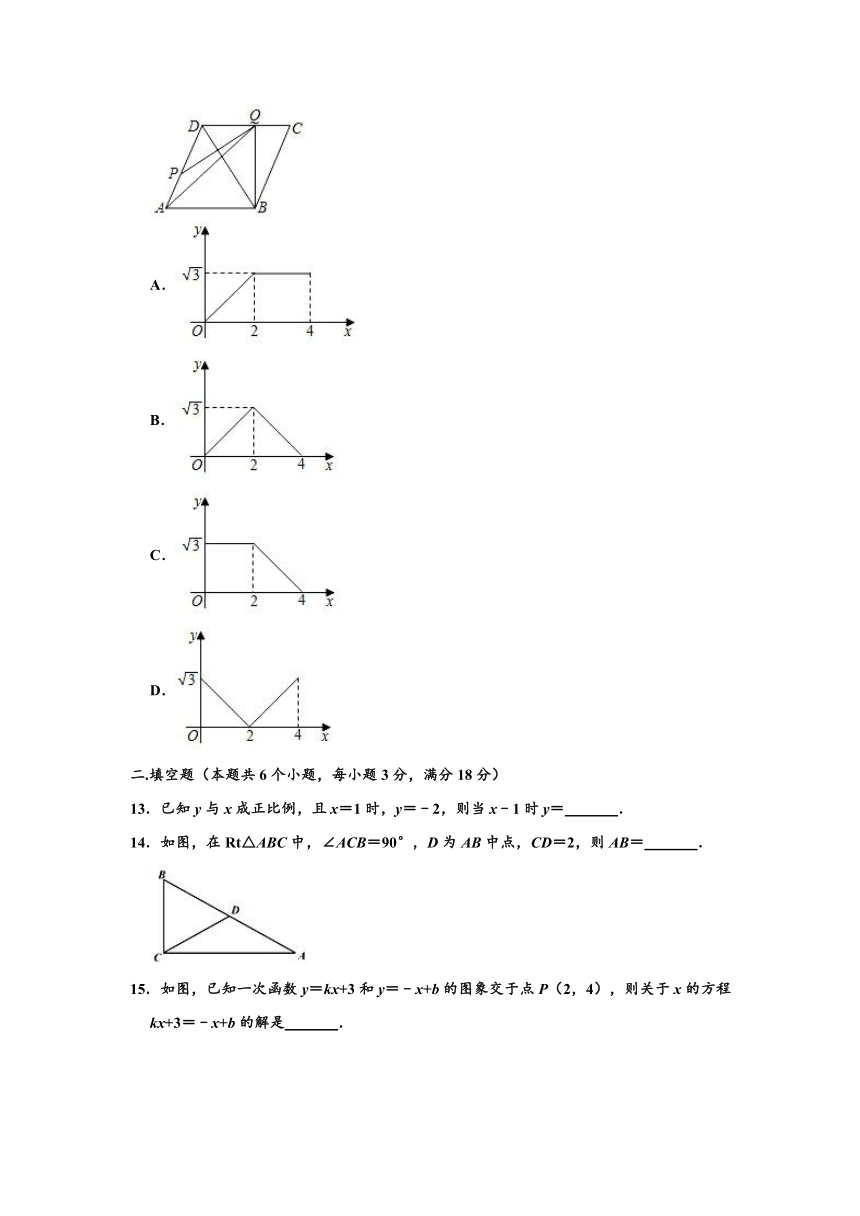
1.函数y=中自变量x的取值范围为( )
A.x>1 B.x≠1 C.x≥1 D.任意实数
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
4.如图,在?ABCD中,BE平分∠ABC,若∠D=64°,则∠AEB等于 .
5.下列能够判定一个四边形是平行四边形的条件是( )
A.一对邻角的和为180° B.两条对角线互相垂直
C.一组对角相等 D.两条对角线互相平分
6.正比例函数y=2x的图象向左平移1个单位后所得函数解析式为( )
A.y=2x+1 B.y=2x﹣1 C.y=2x+2 D.y=2x﹣2
7.某校要从四名学生中选拔一名参加市“风华小主播”大赛,在校的“挑战赛”中,四名学生的平均成绩x和方差如表所示,如果要选一名成绩高且发挥稳定的学生参赛,那么应选的学生是( )
甲 乙 丙 丁
8 9 9 8
s2 1 1.2 1 1.3
A.甲 B.乙 C.丙 D.丁
8.对一组数据:2,2,1,3,3分析不正确的是( )
A.中位数是1 B.众数是3和2
C.平均数是2.2 D.方差是0.56
9.检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
10.根据图所示的程序计算变量y的值,若输入自变量x的值为,则输出的结果是( )
A. B. C. D.
11.下列关于一次函数y=﹣x+2的图象性质的说法中,不正确的是( )
A.直线与x轴交点的坐标是(0,2)
B.直线经过第一、二、四象限
C.y随x的增大而减小
D.与坐标轴围成的三角形面积为2
12.如图,在一个内角为60°的菱形ABCD中,AB=2,点P以每秒1cm的速度从点A出发,沿AD→DC的路径运动,到点C停止,过点P作PQ⊥BD,PQ与边AD(或边CD)交于点Q,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象大致是( )
A.
B.
C.
D.
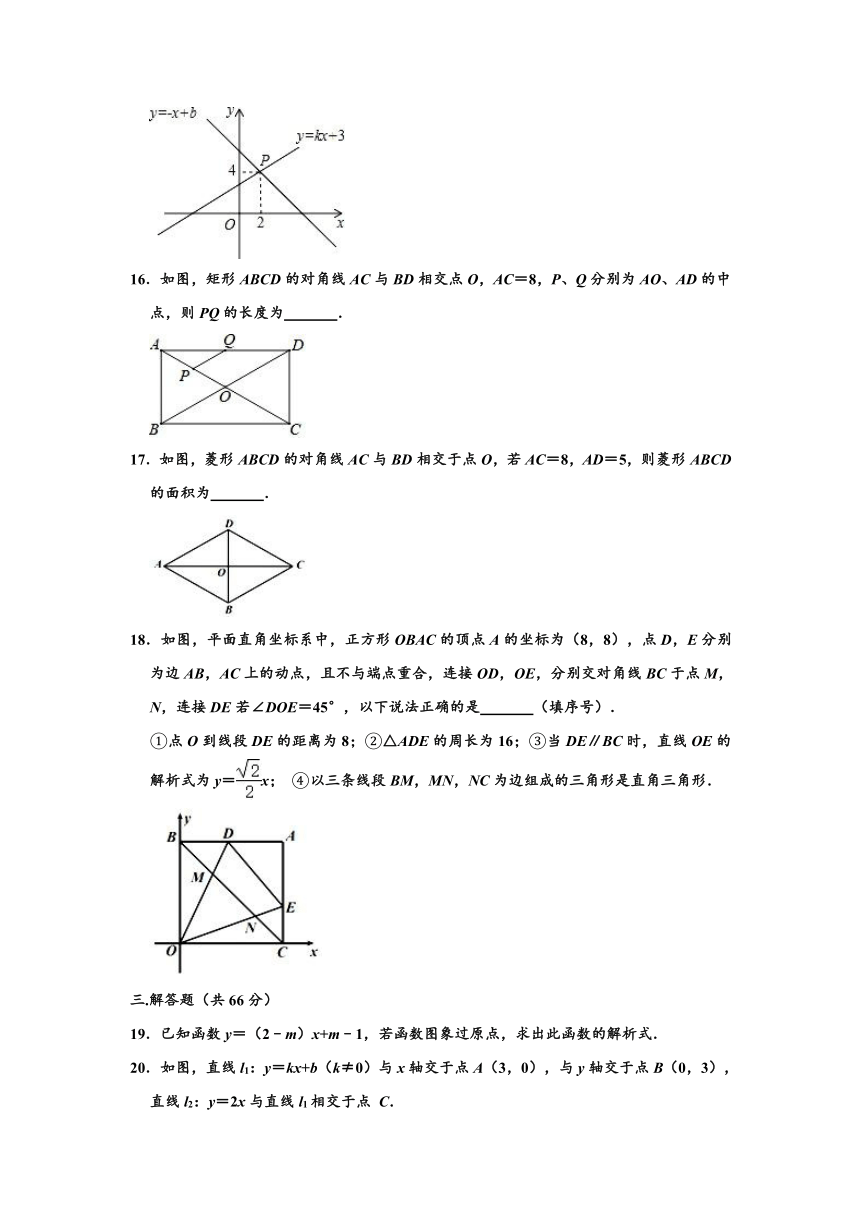
二.填空题(本题共6个小题,每小题3分,满分18分)
13.已知y与x成正比例,且x=1时,y=﹣2,则当x﹣1时y= .
14.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=2,则AB= .
15.如图,已知一次函数y=kx+3和y=﹣x+b的图象交于点P(2,4),则关于x的方程kx+3=﹣x+b的解是 .
16.如图,矩形ABCD的对角线AC与BD相交点O,AC=8,P、Q分别为AO、AD的中点,则PQ的长度为 .
17.如图,菱形ABCD的对角线AC与BD相交于点O,若AC=8,AD=5,则菱形ABCD的面积为 .
18.如图,平面直角坐标系中,正方形OBAC的顶点A的坐标为(8,8),点D,E分别为边AB,AC上的动点,且不与端点重合,连接OD,OE,分别交对角线BC于点M,N,连接DE若∠DOE=45°,以下说法正确的是 (填序号).
①点O到线段DE的距离为8;②△ADE的周长为16;③当DE∥BC时,直线OE的解析式为y=x; ④以三条线段BM,MN,NC为边组成的三角形是直角三角形.
三.解答题(共66分)
19.已知函数y=(2﹣m)x+m﹣1,若函数图象过原点,求出此函数的解析式.
20.如图,直线l1:y=kx+b(k≠0)与x轴交于点A(3,0),与y轴交于点B(0,3),直线l2:y=2x与直线l1相交于点 C.
(1)求直线l1的解析式;
(2)求点C的坐标和△AOC的面积.
21.某校学生会向全校2400名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图统计图1和图2,请根据相关信息,解答系列问题:
(1)本次接受随机抽样调查的学生人数为 人,图1中m的值是 .
(2)求本次调查获取的样本数据的平均数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
22.已知一次函数y=kx+b的图象平行于y=﹣2x+1,且过点(2,﹣1),求:
(1)这个一次函数的解析式;
(2)画出该一次函数的图象:根据图象回答:当x取何值时不等式k+b>3?
23.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
24.4月23日是世界读书日,某校为了营造读书好、好读书、读好书的书香校园,决定采购《简?爱》、《小词大雅》两种图书供学生阅读.通过了解,购买2本《简?爱》和3本《小词大雅》共需168元,购买3本(简?爱》和2本《小词大雅》共需172元.
(1)求一本《简?爱》和《小词大雅》的价格分别是多少元?
(2)若该校计划购买两种图书共300本,其中《简?爱》的数量不多于《小词大雅》数量,且不少于100件.购买《简?爱》m本,求总费用W元与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,学校在团购书籍时,商家店铺中《简?爱》正进行书籍促销活动,每本书箱降价a元 (0<a<8),求学校购书的的最低总费用W1的值.
25.如图,在平面直角坐标系中,矩形OABC的三个顶点A,O,C在坐标轴上,矩形的面积为12,对角线AC所在直线的解析式为y=kx﹣4k(k≠0).
(1)求A,C的坐标;
(2)若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;
(3)在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
26.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形、正方形”中,一定是“十字形”的有 ;
②若凸四边形ABCD是“十字形”,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O,当﹣1≤S四边形≤2﹣2时,求BD的取值范围;
(3)如图2,以“十字形”ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:①=+;②=+;③“十字形”ABCD的周长为32;④∠ABC=60°;若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s的速度沿线段EF匀速运动到点F,再以2cm/s的速度沿线段FB匀速运动到点B,到达点B后停止运动,当点P沿上述路线运动到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
参考答案
一、选择题
1.A; 2.A; 3.A; 4.; 5.A; 6.A; 7.A; 8.A; 9.A; 10.A; 11.A; 12.A;
一.选择题(共12小题).
1.函数y=中自变量x的取值范围为( )
A.x>1 B.x≠1 C.x≥1 D.任意实数
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
4.如图,在?ABCD中,BE平分∠ABC,若∠D=64°,则∠AEB等于 .
5.下列能够判定一个四边形是平行四边形的条件是( )
A.一对邻角的和为180° B.两条对角线互相垂直
C.一组对角相等 D.两条对角线互相平分
6.正比例函数y=2x的图象向左平移1个单位后所得函数解析式为( )
A.y=2x+1 B.y=2x﹣1 C.y=2x+2 D.y=2x﹣2
7.某校要从四名学生中选拔一名参加市“风华小主播”大赛,在校的“挑战赛”中,四名学生的平均成绩x和方差如表所示,如果要选一名成绩高且发挥稳定的学生参赛,那么应选的学生是( )
甲 乙 丙 丁
8 9 9 8
s2 1 1.2 1 1.3
A.甲 B.乙 C.丙 D.丁
8.对一组数据:2,2,1,3,3分析不正确的是( )
A.中位数是1 B.众数是3和2
C.平均数是2.2 D.方差是0.56
9.检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
10.根据图所示的程序计算变量y的值,若输入自变量x的值为,则输出的结果是( )
A. B. C. D.
11.下列关于一次函数y=﹣x+2的图象性质的说法中,不正确的是( )
A.直线与x轴交点的坐标是(0,2)
B.直线经过第一、二、四象限
C.y随x的增大而减小
D.与坐标轴围成的三角形面积为2
12.如图,在一个内角为60°的菱形ABCD中,AB=2,点P以每秒1cm的速度从点A出发,沿AD→DC的路径运动,到点C停止,过点P作PQ⊥BD,PQ与边AD(或边CD)交于点Q,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象大致是( )
A.
B.
C.
D.
二.填空题(本题共6个小题,每小题3分,满分18分)
13.已知y与x成正比例,且x=1时,y=﹣2,则当x﹣1时y= .
14.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=2,则AB= .
15.如图,已知一次函数y=kx+3和y=﹣x+b的图象交于点P(2,4),则关于x的方程kx+3=﹣x+b的解是 .
16.如图,矩形ABCD的对角线AC与BD相交点O,AC=8,P、Q分别为AO、AD的中点,则PQ的长度为 .
17.如图,菱形ABCD的对角线AC与BD相交于点O,若AC=8,AD=5,则菱形ABCD的面积为 .
18.如图,平面直角坐标系中,正方形OBAC的顶点A的坐标为(8,8),点D,E分别为边AB,AC上的动点,且不与端点重合,连接OD,OE,分别交对角线BC于点M,N,连接DE若∠DOE=45°,以下说法正确的是 (填序号).
①点O到线段DE的距离为8;②△ADE的周长为16;③当DE∥BC时,直线OE的解析式为y=x; ④以三条线段BM,MN,NC为边组成的三角形是直角三角形.
三.解答题(共66分)
19.已知函数y=(2﹣m)x+m﹣1,若函数图象过原点,求出此函数的解析式.
20.如图,直线l1:y=kx+b(k≠0)与x轴交于点A(3,0),与y轴交于点B(0,3),直线l2:y=2x与直线l1相交于点 C.
(1)求直线l1的解析式;
(2)求点C的坐标和△AOC的面积.
21.某校学生会向全校2400名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图统计图1和图2,请根据相关信息,解答系列问题:
(1)本次接受随机抽样调查的学生人数为 人,图1中m的值是 .
(2)求本次调查获取的样本数据的平均数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
22.已知一次函数y=kx+b的图象平行于y=﹣2x+1,且过点(2,﹣1),求:
(1)这个一次函数的解析式;
(2)画出该一次函数的图象:根据图象回答:当x取何值时不等式k+b>3?
23.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
24.4月23日是世界读书日,某校为了营造读书好、好读书、读好书的书香校园,决定采购《简?爱》、《小词大雅》两种图书供学生阅读.通过了解,购买2本《简?爱》和3本《小词大雅》共需168元,购买3本(简?爱》和2本《小词大雅》共需172元.
(1)求一本《简?爱》和《小词大雅》的价格分别是多少元?
(2)若该校计划购买两种图书共300本,其中《简?爱》的数量不多于《小词大雅》数量,且不少于100件.购买《简?爱》m本,求总费用W元与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,学校在团购书籍时,商家店铺中《简?爱》正进行书籍促销活动,每本书箱降价a元 (0<a<8),求学校购书的的最低总费用W1的值.
25.如图,在平面直角坐标系中,矩形OABC的三个顶点A,O,C在坐标轴上,矩形的面积为12,对角线AC所在直线的解析式为y=kx﹣4k(k≠0).
(1)求A,C的坐标;
(2)若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;
(3)在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
26.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形、正方形”中,一定是“十字形”的有 ;
②若凸四边形ABCD是“十字形”,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O,当﹣1≤S四边形≤2﹣2时,求BD的取值范围;
(3)如图2,以“十字形”ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:①=+;②=+;③“十字形”ABCD的周长为32;④∠ABC=60°;若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s的速度沿线段EF匀速运动到点F,再以2cm/s的速度沿线段FB匀速运动到点B,到达点B后停止运动,当点P沿上述路线运动到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
参考答案
一、选择题
1.A; 2.A; 3.A; 4.; 5.A; 6.A; 7.A; 8.A; 9.A; 10.A; 11.A; 12.A;
同课章节目录
