2019-2020学年湖南省长沙市雨花区中雅培粹学校八年级下学期期中数学试卷 (含部分答案)
文档属性
| 名称 | 2019-2020学年湖南省长沙市雨花区中雅培粹学校八年级下学期期中数学试卷 (含部分答案) | 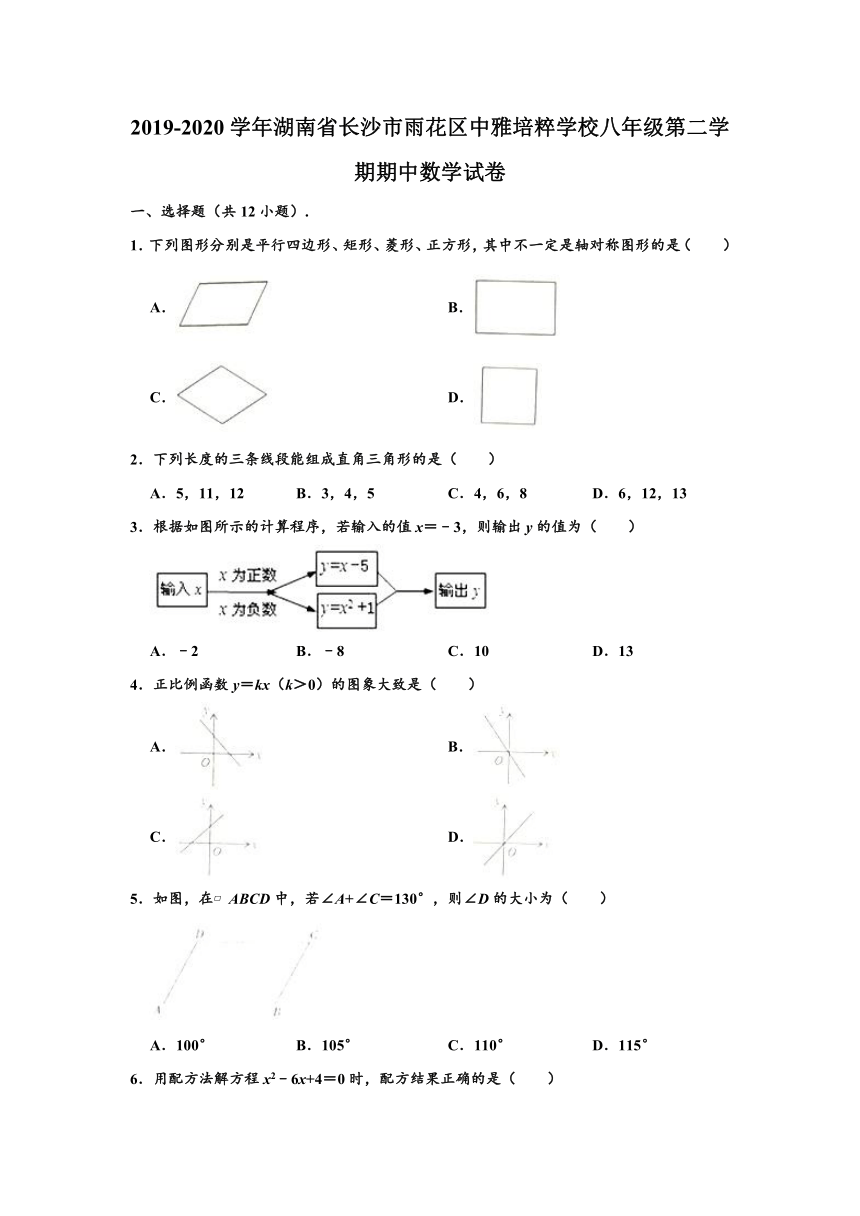 | |
| 格式 | doc | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 06:54:25 | ||
图片预览



文档简介
2019-2020学年湖南省长沙市雨花区中雅培粹学校八年级第二学期期中数学试卷
一、选择题(共12小题).
1.下列图形分别是平行四边形、矩形、菱形、正方形,其中不一定是轴对称图形的是( )
A. B.
C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.3,4,5 C.4,6,8 D.6,12,13
3.根据如图所示的计算程序,若输入的值x=﹣3,则输出y的值为( )
A.﹣2 B.﹣8 C.10 D.13
4.正比例函数y=kx(k>0)的图象大致是( )
A. B.
C. D.
5.如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
A.100° B.105° C.110° D.115°
6.用配方法解方程x2﹣6x+4=0时,配方结果正确的是( )
A.(x﹣3)2=5 B.(x﹣3)2=13 C.(x﹣6)2=32 D.(x﹣6)2=40
7.如图,在?ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为( )
A.10 B.8 C.6 D.4
8.某农业大镇2018年葡萄总产量为1.2万吨,预计2020年葡萄总产量达到1.6万吨,求葡萄总产量的年平均增长率,设葡萄总产量的年平均增长率为x,则可列方程为( )
A.1.2 (1+x)2=1.6 B.1.6 (1﹣x) 2=1.2
C.1.2 (1+2x)=1.6 D.1.2(1+x2)=1.6
9.如图所示,在?ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
10.甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,下列说法错误的是( )
A.甲、乙同学都骑行了18km
B.甲同学比乙同学先到达B地
C.甲停留前、后的骑行速度相同
D.乙的骑行速度是12km/h
11.若关于x的元二次方程(k﹣2)x2+2x﹣1=0有两个不相等的实数根,则实数k的满足( )
A.k>1 B.k>1且k≠2 C.k≤1 D.k≥1且k≠2
12.如图,点E为矩形ABCD的边BC长上的点,作DF⊥AE于点F,且满足DF=AB.下面结论:
①DE平分∠AEC;
②△ADE为等腰三角形;
③AF=AB;
④AE=BE+EF.其中正确的结论有多少个( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6小题,每小题3分,满分18分)
13.函数y=的自变量x的取值范围是 .
14.若x=﹣1是关于x的一元二次方程x2+3x+m+1=0的一个解,则m的值为 .
15.已知菱形ABCD的两条对角线AC=6,BD=8,则菱形的边长BC= .
16.已知正比例函数y=3x,当x的取值范围是﹣3≤x≤4,则y的取值范围是 .
17.如图,将长方形ABCD沿对角线AC折叠,得到如图所示的图形,点B的对应点是点B'
,B′C与AD交于点E.若AB=4,BC=8,则AE的长是 .
18.如图,等边△ABC中,AB=10,点E为AC中点,D是线段BE上的一个动点,则CD+BD的最小值是 .
三、解答题(共8小题,满分66分)
19.解下列方程:
(1)x2﹣4x+3=0;
(2)3x2+5x﹣2=0.
20.已知点(﹣4,2)在正比例函数y=kx的图象上.
(1)求该正比例函数的解析式;
(2)若点(﹣1,m)在该函数的图象上,求出m的值.
21.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点.当它靠在另一侧墙上时,梯子的顶端在D点,已知梯子长2.5m,D点到地面的垂直距离DE=1.5m,两墙的距离CE长3.5m.求B点到地面的垂直距离BC.
22.已知关于x的一元二次方程x2+2mx+m2+m=0有两个实数根.
(1)求m的取值范围;
(2)设x1,x2是方程的两根,且x12+x22=12,求m的值.
23.某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元,为迎接“六?一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.设商店降价x元.
(1)降价x元后,每一件童装的利润为 (元),每天可以卖出去的童装件数为 (件)(用含x的代数式表示);
(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
24.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D.DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO;
(2)求证:四边形ABCD是菱形;
(3)若DE=AB=2,求菱形ABCD的面积.
25.如图,正方形ABCD中,点M是边BC异于点B、C的一点,AM的垂直平分线分别交AB、CD、BD于E、F、K,连接AK、MK.
(1)求证:KA=KM;
(2)请求出:∠AKM的度数;
(3)试猜想线段AE、DF、BM之间的数量关系并说明理由.
26.在平面直角坐标系xOy中,图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小,设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图1,矩形ABCD为△DEF的投影矩形,其投影比k=.
(1)如图2,若点A (1,3),B (3,6),则△OAB投影比k的值为 ;
(2)已知点M(﹣2,0),点N (2,1),且△MPN投影比k=,则P点坐标可能是 (填写序号);
①(﹣1,3);②(2,﹣2);③(3,3);④(6,﹣5).
(3)已知点E (3,2),在直线y=2x上有一点F (5,a)和一动点P(m,n)且m<3,是否存在这样的m,使得△PEF的投影比k为定值?若存在,请求出m的范围及定值k;若不存在,请说明理由.
参考答案
一、选择题
1.A; 2.A; 3.A; 4.A; 5.A; 6.A; 7.A; 8.A; 9.A; 10.A; 11.A; 12.A;
一、选择题(共12小题).
1.下列图形分别是平行四边形、矩形、菱形、正方形,其中不一定是轴对称图形的是( )
A. B.
C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.3,4,5 C.4,6,8 D.6,12,13
3.根据如图所示的计算程序,若输入的值x=﹣3,则输出y的值为( )
A.﹣2 B.﹣8 C.10 D.13
4.正比例函数y=kx(k>0)的图象大致是( )
A. B.
C. D.
5.如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
A.100° B.105° C.110° D.115°
6.用配方法解方程x2﹣6x+4=0时,配方结果正确的是( )
A.(x﹣3)2=5 B.(x﹣3)2=13 C.(x﹣6)2=32 D.(x﹣6)2=40
7.如图,在?ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为( )
A.10 B.8 C.6 D.4
8.某农业大镇2018年葡萄总产量为1.2万吨,预计2020年葡萄总产量达到1.6万吨,求葡萄总产量的年平均增长率,设葡萄总产量的年平均增长率为x,则可列方程为( )
A.1.2 (1+x)2=1.6 B.1.6 (1﹣x) 2=1.2
C.1.2 (1+2x)=1.6 D.1.2(1+x2)=1.6
9.如图所示,在?ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
10.甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,下列说法错误的是( )
A.甲、乙同学都骑行了18km
B.甲同学比乙同学先到达B地
C.甲停留前、后的骑行速度相同
D.乙的骑行速度是12km/h
11.若关于x的元二次方程(k﹣2)x2+2x﹣1=0有两个不相等的实数根,则实数k的满足( )
A.k>1 B.k>1且k≠2 C.k≤1 D.k≥1且k≠2
12.如图,点E为矩形ABCD的边BC长上的点,作DF⊥AE于点F,且满足DF=AB.下面结论:
①DE平分∠AEC;
②△ADE为等腰三角形;
③AF=AB;
④AE=BE+EF.其中正确的结论有多少个( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6小题,每小题3分,满分18分)
13.函数y=的自变量x的取值范围是 .
14.若x=﹣1是关于x的一元二次方程x2+3x+m+1=0的一个解,则m的值为 .
15.已知菱形ABCD的两条对角线AC=6,BD=8,则菱形的边长BC= .
16.已知正比例函数y=3x,当x的取值范围是﹣3≤x≤4,则y的取值范围是 .
17.如图,将长方形ABCD沿对角线AC折叠,得到如图所示的图形,点B的对应点是点B'
,B′C与AD交于点E.若AB=4,BC=8,则AE的长是 .
18.如图,等边△ABC中,AB=10,点E为AC中点,D是线段BE上的一个动点,则CD+BD的最小值是 .
三、解答题(共8小题,满分66分)
19.解下列方程:
(1)x2﹣4x+3=0;
(2)3x2+5x﹣2=0.
20.已知点(﹣4,2)在正比例函数y=kx的图象上.
(1)求该正比例函数的解析式;
(2)若点(﹣1,m)在该函数的图象上,求出m的值.
21.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点.当它靠在另一侧墙上时,梯子的顶端在D点,已知梯子长2.5m,D点到地面的垂直距离DE=1.5m,两墙的距离CE长3.5m.求B点到地面的垂直距离BC.
22.已知关于x的一元二次方程x2+2mx+m2+m=0有两个实数根.
(1)求m的取值范围;
(2)设x1,x2是方程的两根,且x12+x22=12,求m的值.
23.某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元,为迎接“六?一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.设商店降价x元.
(1)降价x元后,每一件童装的利润为 (元),每天可以卖出去的童装件数为 (件)(用含x的代数式表示);
(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
24.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D.DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO;
(2)求证:四边形ABCD是菱形;
(3)若DE=AB=2,求菱形ABCD的面积.
25.如图,正方形ABCD中,点M是边BC异于点B、C的一点,AM的垂直平分线分别交AB、CD、BD于E、F、K,连接AK、MK.
(1)求证:KA=KM;
(2)请求出:∠AKM的度数;
(3)试猜想线段AE、DF、BM之间的数量关系并说明理由.
26.在平面直角坐标系xOy中,图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小,设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图1,矩形ABCD为△DEF的投影矩形,其投影比k=.
(1)如图2,若点A (1,3),B (3,6),则△OAB投影比k的值为 ;
(2)已知点M(﹣2,0),点N (2,1),且△MPN投影比k=,则P点坐标可能是 (填写序号);
①(﹣1,3);②(2,﹣2);③(3,3);④(6,﹣5).
(3)已知点E (3,2),在直线y=2x上有一点F (5,a)和一动点P(m,n)且m<3,是否存在这样的m,使得△PEF的投影比k为定值?若存在,请求出m的范围及定值k;若不存在,请说明理由.
参考答案
一、选择题
1.A; 2.A; 3.A; 4.A; 5.A; 6.A; 7.A; 8.A; 9.A; 10.A; 11.A; 12.A;
同课章节目录
