六年级下册数学课件-三 综合与实践 复习课件 浙教版 (共48张PPT)
文档属性
| 名称 | 六年级下册数学课件-三 综合与实践 复习课件 浙教版 (共48张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 00:00:00 | ||
图片预览








文档简介
(共48张PPT)
三
综合与实践
复习课件
综合与实践
操场上的数学问题
养蚕中的数学问题
旅游中的数学问题
环境保护中的数学问题
一、关于操场,你能运用已经学过的知识想出哪些数学问题?
施工问题:时间×效率=总量
列队问题:每排人数×排数=总人数
行程问题:时间×速度=路程
面积问题:篮球场面积=长×宽
……
长方体车厢的容积
1.学校用卡车运沙石,卡车的车厢长7米,宽2.4米,高0.6米。一车沙石大约有多少立方米?
长方体的容积=长×宽×高
7×2.4×0.6
=16.8×0.6
=10.08(立方米)
答:一车沙石大约有10.08立方米。
长方体的容积如何计算?
例题
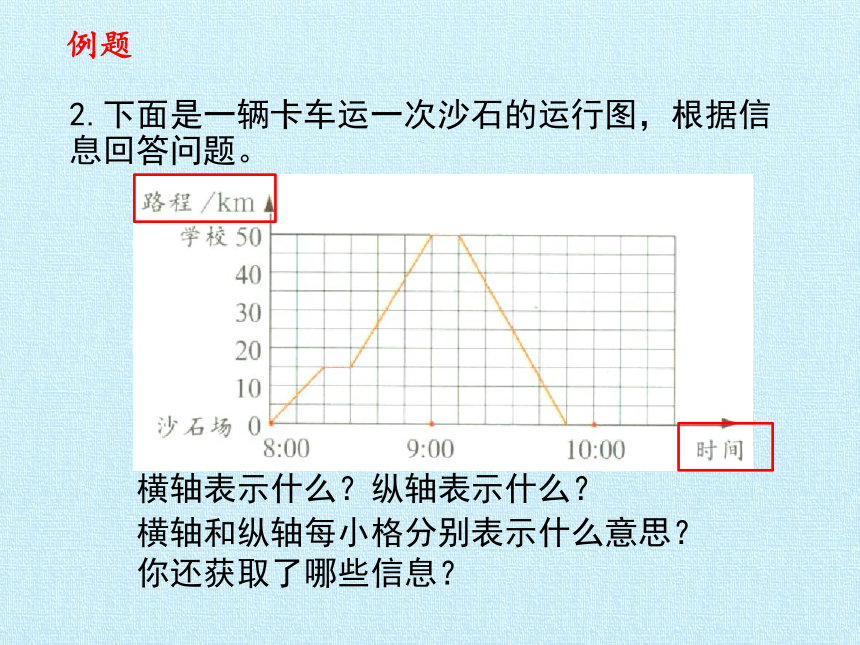
2.下面是一辆卡车运一次沙石的运行图,根据信息回答问题。
横轴和纵轴每小格分别表示什么意思?
横轴表示什么?纵轴表示什么?
你还获取了哪些信息?
例题
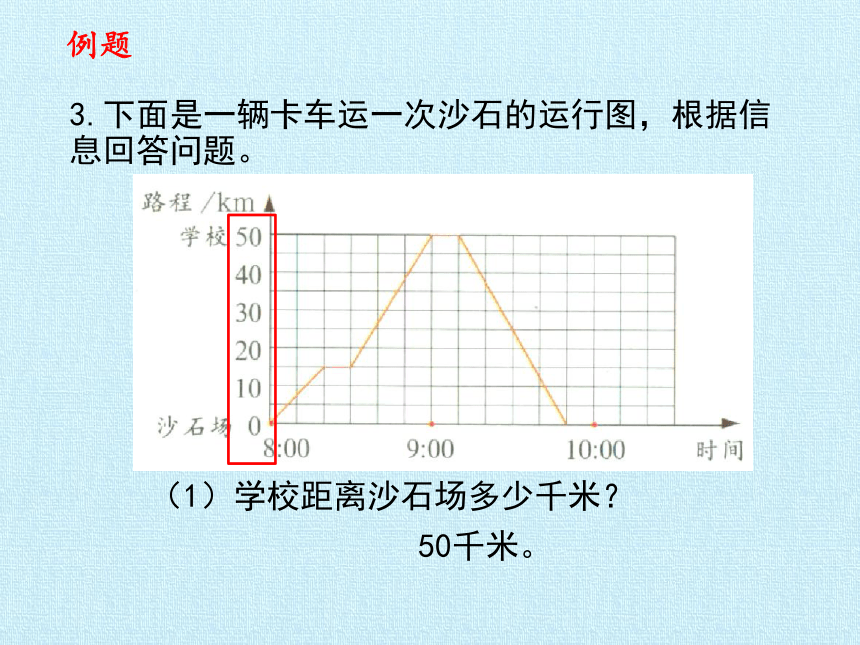
3.下面是一辆卡车运一次沙石的运行图,根据信息回答问题。
50千米。
(1)学校距离沙石场多少千米?
例题
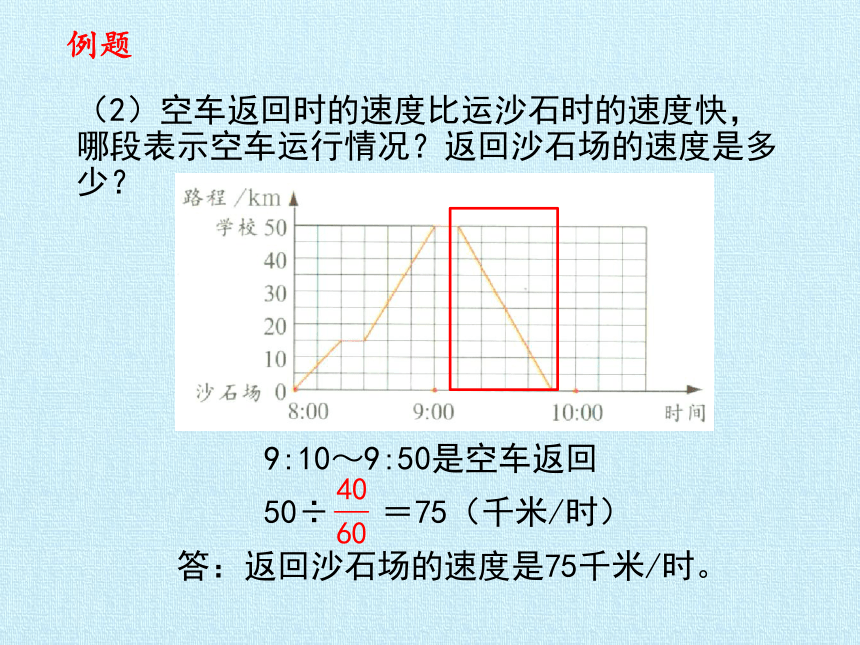
9:10~9:50是空车返回
(2)空车返回时的速度比运沙石时的速度快,哪段表示空车运行情况?返回沙石场的速度是多少?
答:返回沙石场的速度是75千米/时。
50÷
=75(千米/时)
例题
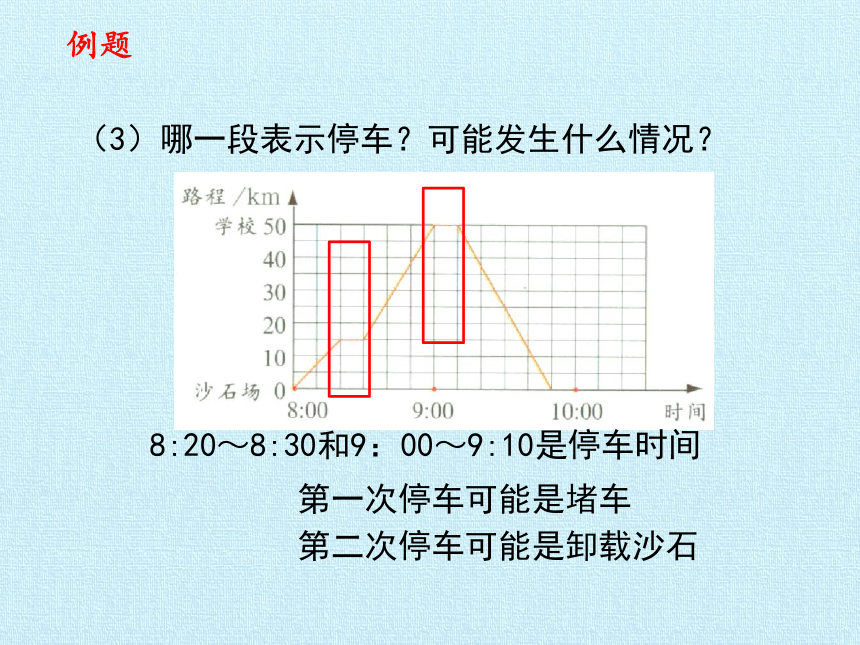
8:20~8:30和9:00~9:10是停车时间
(3)哪一段表示停车?可能发生什么情况?
第一次停车可能是堵车
第二次停车可能是卸载沙石
例题
4.在操场上建一个篮球场。
(1)下图是篮球场的平面示意图。它的实际周长是多少米?
量得平面图中篮球场长约5.6厘米,宽约3厘米
5.6×5=28(米)
3×5=15(米)
(28+15)×2=86(米)
答:它的实际周长是86米。
例题
5.在操场上建一个篮球场。
(2)篮球场平均每平米造价1200元。建这个篮球场大约需要多少元?
28×15×1200
=420×1200
=504000(元)
答:建这个篮球场大约需要504000元。
例题
6.操场上要铺580平方米的沙石,已经铺了5天,每天铺60平方米。剩下的4天铺完,平均每天铺多少平方米?
已铺了多少平方米?
60×5=300(平方米)
还剩多少平方米?
580-300=280(平方米)
280÷4=70(平方米)
如何列综合算式解答?
答:剩下的4天铺完,平均每天铺70平方米。
例题
7.操场上要铺580平方米的沙石,已经铺了5天,每天铺60平方米。剩下的4天铺完,平均每天铺多少平方米?
(580-60×5)÷4
=(580-300)÷4
=280÷4
=70(平方米)
答:剩下的4天铺完,平均每天铺70平方米。
例题
二、关于养蚕,你能运用已经学过的知识想出哪些数学问题?
面积问题:单位面积×数量=总面积
生产问题:数量与产量(质量)成正比
成活率问题:成活率=(总数-未成活数)÷总数×100%
比例尺问题:根据方向、距离和比例尺画平面示意图
……
1.(1)图中的小正方形的边长表示1厘米,1片桑叶的面积大约是多少?
先数满格,
再数不满格。
27.5(平方厘米)
例题
(2)1条蚕体重6克,它的一生消耗了相当于体重
5倍左右的桑叶。1片桑叶重2克左右。1条蚕一生消耗的桑叶大约为多少平方厘米?能铺满一张课桌吗?
一条蚕一生消耗的蚕叶有多重?
6×5=30(克)
一条蚕一生消耗的蚕叶数:
30÷2=15(片)
1片桑叶的面积大约是27.5平方厘米。
27.5×15=412.5(平方厘米)
答:1条蚕一生消耗的桑叶大约为412.5平方厘米。
例题
(2)1条蚕体重6克,它的一生消耗了相当于体重
5倍左右的桑叶。1片桑叶重2克左右。1条蚕一生消耗的桑叶大约为多少平方厘米?能铺满一张课桌吗?
412.5平方厘米=4.125平方分米
答:不能铺满一张课桌。
例题
(3)如果124棵桑树能为6000条蚕提供所需要的
桑叶,聪聪家养9000条蚕,需要多少棵桑树?
6000条蚕
→
124棵树
9000条蚕
→
?棵树
解:设聪聪家养9000条蚕,需要x棵桑树。
6000:124=9000:x
6000x=9000×124
x=1116000÷6000
x=186
答:聪聪家养9000条蚕,需要186棵桑树。
例题
(10000-800)÷10000=92%
(4)佳佳家养蚕10000条,如果未成活的有800条,成活率是多少?改进养殖技术后,成活率可以提高5%。改进养殖技术后,可成活多少条?
答:成活率是92%。
5%+92%=97%
10000×97%=9700(条)
答:改进养殖技术后,可成活9700条。
例题
750-460=290(吨)
(5)某养蚕专业村养蚕情况如下表。
①2008年比2006年增产多少吨?
答:2008年比2006年增产290吨。
年份
2006
2007
数量/张
14720
24000
产量/吨
460
750
例题
它们的比值相等吗?
(5)某养蚕专业村养蚕情况如下表。
②数量与产量是成正比例的量吗?为什么?
14720:460=32
答:两个年份数量与产量的比值相等,所以数量与产量是成正比例的量。
年份
2006
2007
数量/张
14720
24000
产量/吨
460
750
24000:750=32
例题
2.蚕吐丝的速度是30厘米/分。
1条蚕吐丝成茧要60小时。1条蚕所吐的丝可以绕教室几圈?(测量教室的长与宽)
1小时=60分
30×60×60
=1800×60
=108000(厘米)
108000厘米=1080米
如果教室长9米,宽6米,1条蚕所吐的丝可以绕教室几圈?
(9+6)×2=30(米)
1080÷30=36(圈)
答:如果教室长9米,宽6米,1条蚕所吐的丝可以绕教室36圈。
例题
三、关于旅游,你能运用已经学过的知识想出哪些数学问题?
行程问题:时间×速度=路程
比例尺问题:比例尺=图上距离÷实际距离
住店折扣问题:优惠金额=原价×(1-折扣数)
……
1.强强和爸爸、妈妈一家三口自驾车从南苑去北高峰游玩。下图是行车路线图。
例题
2.(1)从南苑到北高峰,某幅图上的距离是8厘米,实际距离是240千米。计算这幅图的比例尺。
240千米=24000000厘米
=
8
24000000
1
3000000
答:这幅图的比例尺是
。
1
3000000
例题
(2)如果行车的平均速度是90千米/时,上午9:00出发,中午12:00前能到达北高峰景区吗?
从南苑到北高峰的实际距离为240千米
240÷90≈2.67(小时)
9:00~12:00为3小时
2.67<3
答:中午12:
00前能到达北高峰景区。
还有哪种解决办法?可以比较路程吗?
例题
(3)按平均耗油量为9升/100千米计算,汽车油箱的容量是60升,出发时油表显示如右图,中途不加油能开到北高峰吗?
240÷100×9
=2.4×9
=21.6(升)
21.6>20
答:中途不加油不能开到北高峰。
例题
240-120=120(千米)
(4)出发1.5小时后车子在服务区停下,强强看到路牌如右图。他们已行多少千米?
答:他们已行驶了120千米。
距北高峰景区120千米
例题
四、关于环保,你能运用已经学过的知识想出哪些数学问题?
面积问题:三角形景区面积=底×高÷2
种群密度=生物个体数÷单位面积。
平均数问题:平均数=各数值之和÷个数
……
1.我国高度重视保护野生动物,林业部门建立了1740多个自然保护区,300多种珍稀濒危野生动物得到了较好的保护。某自然保护区形状近似三角形,如下图。
(1)该自然保护区的面积大约是多少平方千米?合多少公顷?
150×120÷2
=18000÷2
=9000(平方千米)
9000平方千米=900000(公顷)
答:自然保护区的面积大约是9000平方千米,合900000公顷。
例题
(2)一定范围内生物个体的数量称为种群密度。它的计算方法是:
种群密度=生物个体数÷单位面积。
①动物学家在该自然保护区5公顷的范围发现有9只梅花鹿。梅花鹿的种群密度是每公顷几只?
9÷5=1.8(只/公顷)
答:梅花鹿的种群密度是每公顷1.8只。
例题
(2)一定范围内生物个体的数量称为种群密度计算方法是:种群密度=生物个体数÷单位面积。
②估计这个自然保护区内有多少只梅花鹿?
1.8×900000=1620000(只)
答:这个自然保护区内大约有1620000只梅花鹿。
梅花鹿的种群密度是每公顷1.8只。
这个自然保护区的面积大约是900000公顷。
例题
(2)一定范围内生物个体的数量称为种群密度计算方法是:种群密度=生物个体数÷单位面积。
③调查发现,这个自然保护区内红松的种密度是29棵/公顷。计算该自然保护区一共有多少棵红松。
29×900000=26100000(只)
答:该自然保护区一共有26100000棵红松。
例题
2.从天空往下看,热带雨林的树木就像城市中高低不同的楼房。其中长着许多参天大树,高达70米,它们的树干很粗,20多个成年人伸开双臂手拉手,刚刚能围住。
(1)一层楼房的高度按3.2米计算,70米高的树相当于几层楼高?
70÷3.2=21.875(层)
答:70米高的树相当于22层楼高。
≈22(层)
例题
2.(2)平均每个成年人从左手中指尖到右手中指的距离为1.6米。解释平均1.6米表示的意思。
1.6米是平均数。
例题
1.操场长120米,宽80米。现在要扩大操场面积,长不变,宽增加20米。扩大后的操场面积将比原来增加百分之几?
画出示意图。
120×80=9600(平方米)
120米
80米
20米
原来操场的面积是多少?
120×20=2400(平方米)
扩大的面积是多少?
2400÷9600×100%=25%
扩大的面积占原来面积的百分之几?
练习巩固
2.同学们在操场上进行队列训练,每排18人,可以排成18排。如果每排18人,可以排多少排?
每排人数×排数=总人数
变化的哪几个量?哪个量没有变?
解:设每排可以排x人。
24×18=18x
x=24×18÷18
x=24
答:每排可以排24人。
3.操场跑道一圈长400米。强强与聪聪在跑道上练习跑步,他们从同一起点出发,背向而行。强强先跑,每分钟跑150米,1分钟后,聪聪开始跑,她跑了1分钟后和强强相遇。聪聪每分钟跑多少米?
150+两人合跑路程=400
400-150-150
=250-150
=100(米)
答:聪聪每分钟跑100米。
150+聪聪的路程
4.篮球架高2米。佳佳在某时刻测得篮球架的影子长40厘米,旁边一棵大树的影子长90厘米。大树高多少米?
解:设大树高x米。
答:这棵大树高4.5米。
2:0.4=x:0.9
篮球架高度:篮球架影长=大树高度:大树影长
0.4x=2×0.9
x=1.8÷0.4
x=4.5
40厘米=0.4米
90厘米=0.9米
如何列综合算式解答?
围巾占所需蚕茧总数的几分之几?
(2)用蚕丝做一条领带和一条围巾,共需770个蚕茧,做一条领带占
。做一条围巾需多少个蚕茧?
770×(1-
)
=770×
=660(个)
答:做一条围巾需660个蚕茧。
(3)做围巾的面料中含蚕丝42%。用210千克蚕丝可以加工多少千克这种面料?
面料质量
→
“1”
210÷42%=500(千克)
答:用210千克蚕丝可以加工500千克这种面料。
210克蚕丝
→
“42%”
(4)用蚕丝加工领带,要求10天完成。前3天加工510条,完成了计划的
。照这样计算,可以提前几天完成任务?
3(10-x)=15
解:设可以提前x天完成任务。
30-3x=15
3x=15
x=5
答:可以提前5天完成任务。
5.桑园的正南方向500米处有一个养蚕基地,村庄在桑园东偏北40。方向800米处。试用合理的比例尺画出示意图。
比例尺:1:10000
桑园
5厘米
养蚕基地
40°
8厘米
村庄
6.(1)强强一家入住北高峰宾馆,房价如图。强强一家订双人标间和单人间各一间,住两天。如果按上面的标价打八五折,可优惠多少元?
住房总金额是多少?
宾馆房价
双人标间:238元
单人间:180元
238+180=416(元)
416×(1-0.85)
=416×0.15
=62.4(元)
答:可优惠62.4元。
(2)景区门票价格为:成人票20元,儿童票半价。如果买家庭套票(两个成人、一个小孩)可节约20%,家庭套票定价多少元?
20÷2=10(元)
50×(1-20%)=40(元)
20×2+10=50(元)
答:家庭套票定价40元。
(3)从景区入口到山顶可以走石阶路,也可以乘缆车。据统计,景区某日有60%的游客乘坐缆车,比走路的多400人。这天景区的游客共有多少人?
坐缆车人数-走石阶路人数=400
解:设这天景区的游客共有x人。
答:这天景区的游客共有2000人。
60%x×(1-60%)x=400
0.6x-0.4x=400
x=400÷0.2
x=2000
7.植物通过它们的叶子散失水分,一片叶子散失水分的多少一般与它的面积大小有关。下表显示了平均每天每平方厘米叶面散失的水分。(单位:毫克)。
桉树
红千层
橡树
悬铃木
29
33
42
38
(1)把一片叶子做成标本粘在长0.8分米、宽0.6分米的长方形纸上,叶子的面积大约是长方形纸面积的68%。这片叶子的面积是多少平方分米?
0.8×0.6×68%=0.3264(平方分米)
答:这片叶子的面积是0.3264平方分米。
(2)表中几个数据的平均数是多少?
(29+33+42+38)÷4=35.5(毫克/平方厘米)
答:表中几个数据的平均数是35.5。
桉树
红千层
橡树
悬铃木
29
33
42
38
谢
谢
三
综合与实践
复习课件
综合与实践
操场上的数学问题
养蚕中的数学问题
旅游中的数学问题
环境保护中的数学问题
一、关于操场,你能运用已经学过的知识想出哪些数学问题?
施工问题:时间×效率=总量
列队问题:每排人数×排数=总人数
行程问题:时间×速度=路程
面积问题:篮球场面积=长×宽
……
长方体车厢的容积
1.学校用卡车运沙石,卡车的车厢长7米,宽2.4米,高0.6米。一车沙石大约有多少立方米?
长方体的容积=长×宽×高
7×2.4×0.6
=16.8×0.6
=10.08(立方米)
答:一车沙石大约有10.08立方米。
长方体的容积如何计算?
例题
2.下面是一辆卡车运一次沙石的运行图,根据信息回答问题。
横轴和纵轴每小格分别表示什么意思?
横轴表示什么?纵轴表示什么?
你还获取了哪些信息?
例题
3.下面是一辆卡车运一次沙石的运行图,根据信息回答问题。
50千米。
(1)学校距离沙石场多少千米?
例题
9:10~9:50是空车返回
(2)空车返回时的速度比运沙石时的速度快,哪段表示空车运行情况?返回沙石场的速度是多少?
答:返回沙石场的速度是75千米/时。
50÷
=75(千米/时)
例题
8:20~8:30和9:00~9:10是停车时间
(3)哪一段表示停车?可能发生什么情况?
第一次停车可能是堵车
第二次停车可能是卸载沙石
例题
4.在操场上建一个篮球场。
(1)下图是篮球场的平面示意图。它的实际周长是多少米?
量得平面图中篮球场长约5.6厘米,宽约3厘米
5.6×5=28(米)
3×5=15(米)
(28+15)×2=86(米)
答:它的实际周长是86米。
例题
5.在操场上建一个篮球场。
(2)篮球场平均每平米造价1200元。建这个篮球场大约需要多少元?
28×15×1200
=420×1200
=504000(元)
答:建这个篮球场大约需要504000元。
例题
6.操场上要铺580平方米的沙石,已经铺了5天,每天铺60平方米。剩下的4天铺完,平均每天铺多少平方米?
已铺了多少平方米?
60×5=300(平方米)
还剩多少平方米?
580-300=280(平方米)
280÷4=70(平方米)
如何列综合算式解答?
答:剩下的4天铺完,平均每天铺70平方米。
例题
7.操场上要铺580平方米的沙石,已经铺了5天,每天铺60平方米。剩下的4天铺完,平均每天铺多少平方米?
(580-60×5)÷4
=(580-300)÷4
=280÷4
=70(平方米)
答:剩下的4天铺完,平均每天铺70平方米。
例题
二、关于养蚕,你能运用已经学过的知识想出哪些数学问题?
面积问题:单位面积×数量=总面积
生产问题:数量与产量(质量)成正比
成活率问题:成活率=(总数-未成活数)÷总数×100%
比例尺问题:根据方向、距离和比例尺画平面示意图
……
1.(1)图中的小正方形的边长表示1厘米,1片桑叶的面积大约是多少?
先数满格,
再数不满格。
27.5(平方厘米)
例题
(2)1条蚕体重6克,它的一生消耗了相当于体重
5倍左右的桑叶。1片桑叶重2克左右。1条蚕一生消耗的桑叶大约为多少平方厘米?能铺满一张课桌吗?
一条蚕一生消耗的蚕叶有多重?
6×5=30(克)
一条蚕一生消耗的蚕叶数:
30÷2=15(片)
1片桑叶的面积大约是27.5平方厘米。
27.5×15=412.5(平方厘米)
答:1条蚕一生消耗的桑叶大约为412.5平方厘米。
例题
(2)1条蚕体重6克,它的一生消耗了相当于体重
5倍左右的桑叶。1片桑叶重2克左右。1条蚕一生消耗的桑叶大约为多少平方厘米?能铺满一张课桌吗?
412.5平方厘米=4.125平方分米
答:不能铺满一张课桌。
例题
(3)如果124棵桑树能为6000条蚕提供所需要的
桑叶,聪聪家养9000条蚕,需要多少棵桑树?
6000条蚕
→
124棵树
9000条蚕
→
?棵树
解:设聪聪家养9000条蚕,需要x棵桑树。
6000:124=9000:x
6000x=9000×124
x=1116000÷6000
x=186
答:聪聪家养9000条蚕,需要186棵桑树。
例题
(10000-800)÷10000=92%
(4)佳佳家养蚕10000条,如果未成活的有800条,成活率是多少?改进养殖技术后,成活率可以提高5%。改进养殖技术后,可成活多少条?
答:成活率是92%。
5%+92%=97%
10000×97%=9700(条)
答:改进养殖技术后,可成活9700条。
例题
750-460=290(吨)
(5)某养蚕专业村养蚕情况如下表。
①2008年比2006年增产多少吨?
答:2008年比2006年增产290吨。
年份
2006
2007
数量/张
14720
24000
产量/吨
460
750
例题
它们的比值相等吗?
(5)某养蚕专业村养蚕情况如下表。
②数量与产量是成正比例的量吗?为什么?
14720:460=32
答:两个年份数量与产量的比值相等,所以数量与产量是成正比例的量。
年份
2006
2007
数量/张
14720
24000
产量/吨
460
750
24000:750=32
例题
2.蚕吐丝的速度是30厘米/分。
1条蚕吐丝成茧要60小时。1条蚕所吐的丝可以绕教室几圈?(测量教室的长与宽)
1小时=60分
30×60×60
=1800×60
=108000(厘米)
108000厘米=1080米
如果教室长9米,宽6米,1条蚕所吐的丝可以绕教室几圈?
(9+6)×2=30(米)
1080÷30=36(圈)
答:如果教室长9米,宽6米,1条蚕所吐的丝可以绕教室36圈。
例题
三、关于旅游,你能运用已经学过的知识想出哪些数学问题?
行程问题:时间×速度=路程
比例尺问题:比例尺=图上距离÷实际距离
住店折扣问题:优惠金额=原价×(1-折扣数)
……
1.强强和爸爸、妈妈一家三口自驾车从南苑去北高峰游玩。下图是行车路线图。
例题
2.(1)从南苑到北高峰,某幅图上的距离是8厘米,实际距离是240千米。计算这幅图的比例尺。
240千米=24000000厘米
=
8
24000000
1
3000000
答:这幅图的比例尺是
。
1
3000000
例题
(2)如果行车的平均速度是90千米/时,上午9:00出发,中午12:00前能到达北高峰景区吗?
从南苑到北高峰的实际距离为240千米
240÷90≈2.67(小时)
9:00~12:00为3小时
2.67<3
答:中午12:
00前能到达北高峰景区。
还有哪种解决办法?可以比较路程吗?
例题
(3)按平均耗油量为9升/100千米计算,汽车油箱的容量是60升,出发时油表显示如右图,中途不加油能开到北高峰吗?
240÷100×9
=2.4×9
=21.6(升)
21.6>20
答:中途不加油不能开到北高峰。
例题
240-120=120(千米)
(4)出发1.5小时后车子在服务区停下,强强看到路牌如右图。他们已行多少千米?
答:他们已行驶了120千米。
距北高峰景区120千米
例题
四、关于环保,你能运用已经学过的知识想出哪些数学问题?
面积问题:三角形景区面积=底×高÷2
种群密度=生物个体数÷单位面积。
平均数问题:平均数=各数值之和÷个数
……
1.我国高度重视保护野生动物,林业部门建立了1740多个自然保护区,300多种珍稀濒危野生动物得到了较好的保护。某自然保护区形状近似三角形,如下图。
(1)该自然保护区的面积大约是多少平方千米?合多少公顷?
150×120÷2
=18000÷2
=9000(平方千米)
9000平方千米=900000(公顷)
答:自然保护区的面积大约是9000平方千米,合900000公顷。
例题
(2)一定范围内生物个体的数量称为种群密度。它的计算方法是:
种群密度=生物个体数÷单位面积。
①动物学家在该自然保护区5公顷的范围发现有9只梅花鹿。梅花鹿的种群密度是每公顷几只?
9÷5=1.8(只/公顷)
答:梅花鹿的种群密度是每公顷1.8只。
例题
(2)一定范围内生物个体的数量称为种群密度计算方法是:种群密度=生物个体数÷单位面积。
②估计这个自然保护区内有多少只梅花鹿?
1.8×900000=1620000(只)
答:这个自然保护区内大约有1620000只梅花鹿。
梅花鹿的种群密度是每公顷1.8只。
这个自然保护区的面积大约是900000公顷。
例题
(2)一定范围内生物个体的数量称为种群密度计算方法是:种群密度=生物个体数÷单位面积。
③调查发现,这个自然保护区内红松的种密度是29棵/公顷。计算该自然保护区一共有多少棵红松。
29×900000=26100000(只)
答:该自然保护区一共有26100000棵红松。
例题
2.从天空往下看,热带雨林的树木就像城市中高低不同的楼房。其中长着许多参天大树,高达70米,它们的树干很粗,20多个成年人伸开双臂手拉手,刚刚能围住。
(1)一层楼房的高度按3.2米计算,70米高的树相当于几层楼高?
70÷3.2=21.875(层)
答:70米高的树相当于22层楼高。
≈22(层)
例题
2.(2)平均每个成年人从左手中指尖到右手中指的距离为1.6米。解释平均1.6米表示的意思。
1.6米是平均数。
例题
1.操场长120米,宽80米。现在要扩大操场面积,长不变,宽增加20米。扩大后的操场面积将比原来增加百分之几?
画出示意图。
120×80=9600(平方米)
120米
80米
20米
原来操场的面积是多少?
120×20=2400(平方米)
扩大的面积是多少?
2400÷9600×100%=25%
扩大的面积占原来面积的百分之几?
练习巩固
2.同学们在操场上进行队列训练,每排18人,可以排成18排。如果每排18人,可以排多少排?
每排人数×排数=总人数
变化的哪几个量?哪个量没有变?
解:设每排可以排x人。
24×18=18x
x=24×18÷18
x=24
答:每排可以排24人。
3.操场跑道一圈长400米。强强与聪聪在跑道上练习跑步,他们从同一起点出发,背向而行。强强先跑,每分钟跑150米,1分钟后,聪聪开始跑,她跑了1分钟后和强强相遇。聪聪每分钟跑多少米?
150+两人合跑路程=400
400-150-150
=250-150
=100(米)
答:聪聪每分钟跑100米。
150+聪聪的路程
4.篮球架高2米。佳佳在某时刻测得篮球架的影子长40厘米,旁边一棵大树的影子长90厘米。大树高多少米?
解:设大树高x米。
答:这棵大树高4.5米。
2:0.4=x:0.9
篮球架高度:篮球架影长=大树高度:大树影长
0.4x=2×0.9
x=1.8÷0.4
x=4.5
40厘米=0.4米
90厘米=0.9米
如何列综合算式解答?
围巾占所需蚕茧总数的几分之几?
(2)用蚕丝做一条领带和一条围巾,共需770个蚕茧,做一条领带占
。做一条围巾需多少个蚕茧?
770×(1-
)
=770×
=660(个)
答:做一条围巾需660个蚕茧。
(3)做围巾的面料中含蚕丝42%。用210千克蚕丝可以加工多少千克这种面料?
面料质量
→
“1”
210÷42%=500(千克)
答:用210千克蚕丝可以加工500千克这种面料。
210克蚕丝
→
“42%”
(4)用蚕丝加工领带,要求10天完成。前3天加工510条,完成了计划的
。照这样计算,可以提前几天完成任务?
3(10-x)=15
解:设可以提前x天完成任务。
30-3x=15
3x=15
x=5
答:可以提前5天完成任务。
5.桑园的正南方向500米处有一个养蚕基地,村庄在桑园东偏北40。方向800米处。试用合理的比例尺画出示意图。
比例尺:1:10000
桑园
5厘米
养蚕基地
40°
8厘米
村庄
6.(1)强强一家入住北高峰宾馆,房价如图。强强一家订双人标间和单人间各一间,住两天。如果按上面的标价打八五折,可优惠多少元?
住房总金额是多少?
宾馆房价
双人标间:238元
单人间:180元
238+180=416(元)
416×(1-0.85)
=416×0.15
=62.4(元)
答:可优惠62.4元。
(2)景区门票价格为:成人票20元,儿童票半价。如果买家庭套票(两个成人、一个小孩)可节约20%,家庭套票定价多少元?
20÷2=10(元)
50×(1-20%)=40(元)
20×2+10=50(元)
答:家庭套票定价40元。
(3)从景区入口到山顶可以走石阶路,也可以乘缆车。据统计,景区某日有60%的游客乘坐缆车,比走路的多400人。这天景区的游客共有多少人?
坐缆车人数-走石阶路人数=400
解:设这天景区的游客共有x人。
答:这天景区的游客共有2000人。
60%x×(1-60%)x=400
0.6x-0.4x=400
x=400÷0.2
x=2000
7.植物通过它们的叶子散失水分,一片叶子散失水分的多少一般与它的面积大小有关。下表显示了平均每天每平方厘米叶面散失的水分。(单位:毫克)。
桉树
红千层
橡树
悬铃木
29
33
42
38
(1)把一片叶子做成标本粘在长0.8分米、宽0.6分米的长方形纸上,叶子的面积大约是长方形纸面积的68%。这片叶子的面积是多少平方分米?
0.8×0.6×68%=0.3264(平方分米)
答:这片叶子的面积是0.3264平方分米。
(2)表中几个数据的平均数是多少?
(29+33+42+38)÷4=35.5(毫克/平方厘米)
答:表中几个数据的平均数是35.5。
桉树
红千层
橡树
悬铃木
29
33
42
38
谢
谢
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
