四年级下册数学课件-五 代数式与方程 复习课件 浙教版 (共99张PPT)
文档属性
| 名称 | 四年级下册数学课件-五 代数式与方程 复习课件 浙教版 (共99张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 06:27:26 | ||
图片预览











文档简介
(共99张PPT)
五
代数式与方程
复习课件
用字母表示数
简易方程
列方程解应用题
用字母表示数的意义
方程的解
将数值代入式子求值
解方程
列方程解应用题的一般步骤
方程解应用题
知识网络
25.代数式一
在教学中,人们常用字母表示数。想一想,下面的字母分别表示多少?
a×3=27
a=9
=9
5×x+40
=
100
15b-7×b=96
b=12
c=8
x=12
像
a×3,
,
15×b-7×b,5x+40这样含有字母的式子叫代数式。单独一个数或字母也是代数式。
在代数式里,数字和字母、字母和字母相乘时,乘号可以写成“ ”,或省略不写,通常数字写在字母前面。
写做
a.3或3a
.
如:
15×b-7×b
写做15b-7b
x
5×
写做5
x
a×3
1与任何字母相乘时,1可以省略不写。
例如:1×a
可以直接写成a
m×5
可以直接写成5m
练一练
1.如果大螃蟹爬行的速度是a厘米/分,小螃蟹爬行的速度是b厘米/分,它们都爬了5分钟,那么,
(1)大螃蟹爬了多少路径?
(1)大螃蟹爬了5a厘米。
(2)小螃蟹爬了多少路径?
(2)小螃蟹爬了5b厘米。
(3)大螃蟹比小螃蟹多爬了多少路径?
(3)大螃蟹比小螃蟹多爬了(5a-5b)厘米。
(4)一辆公共汽车上原来有x人,到新街口车站下去5人,又上来y人。现在车上有(
)人。
(1)储蓄罐里原来有n元,今天小刚又存入3元,储蓄罐里现在有(
)元。
(2)一件上衣a元,一条裤子比上衣便宜
12元,一条裤子(
)元。
(3)小刚每天看课外书15页,a天共看了(
)页。
n+3
a-12
15a
x-5
+y
练一练
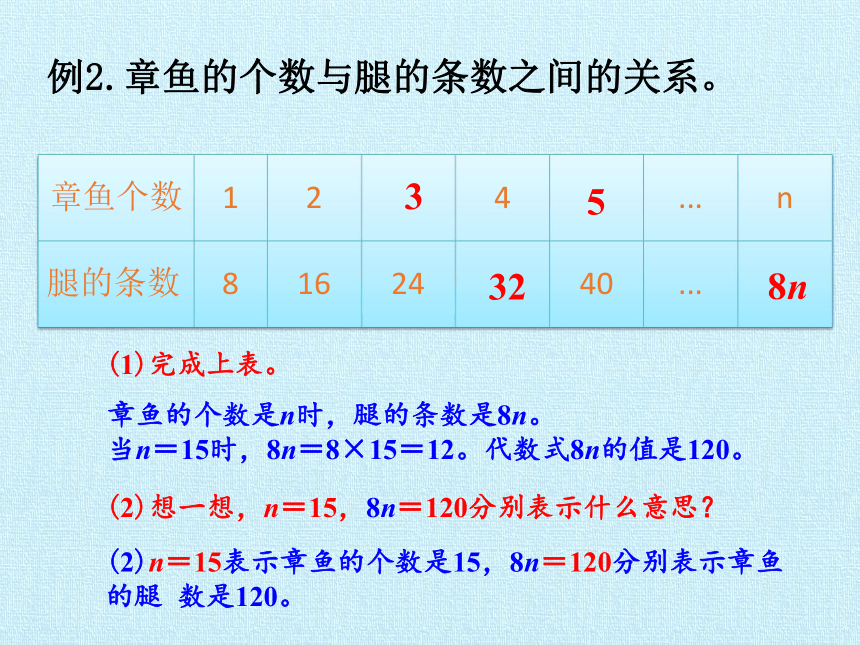
例2.章鱼的个数与腿的条数之间的关系。
章鱼个数
1
2
4
...
n
腿的条数
8
16
24
40
...
(1)完成上表。
章鱼的个数是n时,腿的条数是8n。
当n=15时,8n=8×15=12。代数式8n的值是120。
(2)想一想,n=15,8n=120分别表示什么意思?
(2)n=15表示章鱼的个数是15,8n=120分别表示章鱼的腿
数是120。
3
5
32
8n
巩固练习1:
有n只帆船,每只帆船乘坐a条海马,码头上还有m条海马。有代数式an+m表示海马的总条数。如果a=5,n=7,m=12,写成代数式的值。
解:把a=5,n=7,m=12带入代数式an+m,
得,an
+
m=5×7
+
12=35
+
12=47
爸爸比小明大30岁,爸爸今年n岁,5年后小明几岁?
5年后(5n-30)岁
巩固练习2:
26.代数式二
根据运算定律把下面的图形算式化简:
8×
+5×
3a-2a
8a+5a
=(8+5)×
=13×
=(3-2)a
=a
=(8+5)a
=13a
根据运算定律可以把图形式化简,同样也可以把代数式化简。
例1.螃蟹爬行的速度是a厘米/分,第一次爬行20分钟,第二次爬行30分钟。第二次比第一次多爬行多少厘米?
30a-20a=(30-20)a
=10a
第一次
第二次比第一次多爬行多少厘米?
第二次
随堂练习:
1.化简下列各式。
24b-9b
5x+3x-7
12b+4b+9b
6x-3x+5
=(24-9)b
=15b
=(5+3)x-7
=8x-7
=(12+4+9)b
=25b
=(6-3)x+5
=3x+5
1.写出下面数量关系的代数式,能化简的要化简。
(1)某宾馆某月每天烧煤x千克,4天烧煤都是千克?该月一共烧23天,还要烧煤多少千克?
(2)此宾馆有2人间(2个床位)客房a间,3人间客房b间。一共有多少个床位?
(1)4a千克
(1)19a千克
(2)(2a+3b)个
随堂练习:
巩固练习:化简下面各题。
1.2x+3x-2
=(2+3)x-2
=5x-2
2.m+2m-m
=(1+2-1)m
=2m
3.9x-4x+2x
=(9-4+2)x
=7x
26a+7a-8
=(26+7)a-8
=33a-8
例2.用代数式表示下图中大长方形的面积。(单位:厘米)
1
2
9
a
4
9a+4a=
a
13
长方形的面积是:
长方形的面积是:
9a
4a
(1)一辆汽车从甲开往乙地,速度是x米/分,先行15分钟,中途休息后再行b分钟,离乙地还有150米。
15分钟
行驶的路程
b分钟
行驶的路程
150米
甲
乙
用代数式表示甲、乙两地的路程。
15x+bx+150=(15x+150)米
x米/分钟
随堂练习:
(2)一辆汽车和一辆货车同时从甲乙两地相对开出。汽车的速度是x米/分,货车的速度是y米/分。20分钟后相遇。
用代数式表示相遇时汽车比货车多行的路程。
20x-20y=20(x-y)米
(3)某学校定制一批服装。服装公司用a=10+2n计算一件服装的成本。a表示成本,n表示做一件服装需要的小时数,计算n=2时的成本。(单位:元)
把n=2代入a=10+2n
得:
c=10+2×2
c=14
随堂练习:
(4)A,B两地相距500米,甲车从A地出发已经行a米,剩下的路程如果每分钟行b米,15分钟可到达。
A
500m
am
15bm
B
分别写出两个表示A,B路程的代数式。
分别写出两个表示剩下路程的代数式。
500m
(a+15b)m
15bm
(500-a)m
5.某工厂制作一批课桌,计划x天完成,实际每天制作23个,提前y天完成任务。
(1)写出x-y表示的意义。
(2)用代数式表示这批竹筐的个数。
(3)当x=10,y=2时,求各代数式的值。
(1)x-y表示实际完成任务用的天数。
(2)23(x-y)个。
(3)x-y=10-2=8
(2)23(x-y)
=23×(10-2)
=184
随堂练习:
(1)我国青少年(7~17岁)在1980年平均身高x厘米,到2000年平均身高增长6cm,2000年我国青少年平均身高________厘米。
(2)人的身高可能会相差2cm,在早上最高,晚上最矮。一个人早上身高
b
厘米,晚上身高可能是________厘米。
(3)鸟的骨骼约是体重的0.05~0.06倍,人的骨骼约是体重的0.18倍,一个人重a千克,骨骼约是________千克。
(4)小英家本月的用电量是80千瓦时,交电费c元,那么电费每千瓦时是________元。
x+6
b-2
0.18a
C÷80
拓展练习:
27.认识方程
等式有什么特征?能说说什么样的式子叫做等式吗?
左右两边相等的式子叫做等式。
像2x
=
16,7×2+8=y+8,a+7=9+6这样含有未知数的等式是方程。
讨论:等式与方程有什么关系?
等式
方程
所有的( )都是(
)
有的(
)是(
)
1、试一试:看图列方程
2x=500
12+x=20
500g
2、分别写出两个等式、两个方程,同桌交换检查并更正。
3、看图列方程
x+50=100
5x=50
50g
100g
50g
4、看图列方程。
海马条数:
海马条数:
a
2a
24
a+2a=24
4x=16.8
200+x=450
28.等式的性质
等式有什么特征?能说说什么样的式子叫做等式吗?
左右两边相等的式子叫做等式。
b
a
天平与等式
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
等式的左边
等式的右边
等号
用字母a表示一个
的质量,每个
都重一个单位,右图用等式表示为a=3。
a
=
3
1.从天平左侧和右侧的托盘里分别放进或取出2
个
,你还能用等式表示吗?
a=3
a+2=3+2
a=3
a+2-2=3+2-2
(1)如果天平两侧分别放进或取出5个
、8个
……呢?
a+5=3+5
天平两侧分别放进或取出8个
a+5-5=3+5-5
天平两侧分别放进或取出5个
a+8=3+8
a+8-8=3+8-8
(2)如果用字母b表示一个的
质量,那么a=3b。等式两边都加上2b,怎样表示呢?
a+2b=3b+2b
等式两边都加上或减去同一个数或式,所得的结果仍为等式。这就是等式的性质。
练一练:
1、在
里填数。
35+48=60+23
+48
=+23
42+a=37+b
+a=
+b
+5
+5
-12
-12
40
65
30
25
5a-4=3a+12
2a-0=
0+
+4
-3a
-3a
+4
14
7b+9
=9b
-5
0+
=
-5
-7b
+5
-7b
+5
16
2b
练一练:
1、在
里填数。
联系等式:(1)a+30=c+50
你能变出几个等式?
巩固练习:
a-50-c=30
a-c=50-30
a+30-c=50
(2)判断:已知a=b,c=d
a-2=b-3
(
)
a+c=b+d
(
)
a-b=c-
d
(
)
a+5=c+5
(
)
对
错
对
对
例2.观察天平左侧和右侧的变化,你发现了什么?
a=3
a×2=3×2
a=3
a×2÷2=3×2÷2
从左侧到右侧,天平的左右两侧都扩大2倍,天平仍然平衡。
从右侧到左侧,天平的左右两侧都缩小3倍,天平仍然平衡。
讨论:如果天平两侧都乘或处以3,4,5…,b呢?
等式的两边都乘或除以同一个不为0的数或式,所得的结果仍为等式。这也是等式的性质。
练一练:
1、在
里填数。
3a=5b
15a=
b
8(x+5)=96
(x+5)=
×5
÷8
÷8
×5
25
1
12
2a=3b
a=
b
20(x+3)=60
(x+3)=
×4
÷20
÷20
×4
12
1
3
8
练一练:
1、在
里填数。
3.x÷4=48
x÷4
○(
)
=48
○(
)
4.x
×
4=48
x
×
4
○(
)
=48
○(
)
2.x-4=48
x-4
○
(
)
=48
○
(
)
1.x+4=48
x+4
○
(
)
=48○(
)
在○里填上合适的运算符号,在(
)里填上合适的数。
+
+
15
15
-
15
15
-
÷
4
÷
4
÷
4
4
÷
29.解方程
例1.买某种布料5米,共用去80元。这种布料每米多少元?
如果用
表示这种布料的单价,你能列出图形等式吗?
5×
=80
5×
=80
如果用过x代替
,这个图形算式可以怎么写?
你能求x的值吗?
5x=80
5x=80
解:5x=80
x=80÷5
x=16
等式两边都除以5.
积除以一个因数
使方程左右两边相等的未知数的值叫做方程的解。
检验:把x=16带入方程左边,5×16=80,与方程右边相等,所以x=16使方程的解。
求方程解的过程叫做解方程
练一练1.直接说出x的值。
35+x=100
x÷6=25
21x=63
x-3.5=5.8
42÷x=7
2.5-x=2.5
x=65
x=130
x=3
x=9.3
x
=6
x=0
1.请你画图或举例说说下面这句话的意思:
等式两边都加上(或减去)同一个数,等式仍然成立。
2.看图列方程,并解方程。
y+20=50+20+10
解:y+20=80
y=
80-20
y=60
3.
解方程。
x-9=12
解:x=12+9
x=21
x-12.3=3.8
解:x=3.8+12.3
x=16.1
4.
看图列方程,并解方程。
x+4=19
解:x=19-4
x=15
x-62=486
解:x=486+62
x=548
y+60+50=180
解:y+110=180
y=70
内装x个
19个
原价:x元
降价:62元
现价:486元
60°
50°
y°
1.解方程:18(x+14)=540
解:18(x+14)=540
等式两边都除以18
等式两边都减14
积除以一个因数
和减去一个加数
检验:18×(16+14)=540
x+14=540÷18
x=30-14
x=16
练一练
2.解方程。
2x-5=79
解:2x=79+5
2x=84
x=84÷2
x=42
420-3y=120
解:3y=420-120
3y=300
y=300÷3
y=100
6(43+x)=330
解:43+x=330÷6
43+x=55
x=55-43
x=12
16y=12(y+6)
解:16y=12y+72
6y-12y=72
4y=72
y=18
3.花圃里有铁树、君子兰和腊梅花共260盆。腊梅花的盆数是君子兰的2倍,君子兰的盆数是铁树的3倍。
铁树
君子兰
腊梅花
260盆
1份
3份
(3×2)份
x盆
3x盆
(2×3)x盆
x+3x+(3×2)x=260
解:10x=260
x=26
1.看图列方程,并解方程。
(1)
(2)
18a
20y
24y-20=20y
解:24y-20y=20
4y=20
y=5
15(a+4)
15(a+4)=18a
解:15a+60=18a
18a-15a=60
3a=60
a=20
巩固练习
1.
看图回答问题。
⑴图中哪一段长度是(200-
)米?
⑵图中哪一段长度是(200+
)米?
⑶根据上图,你能列出两个不同的方程吗?
150米
500米
150+
x
=200
150+x+y=500
拓展应用
30.列方程解题(一)
知识回顾
最近悟空有些闷闷不乐,想必是遇到了什么难题,我用千里眼看一下,原来是遇到了一道数学题,可是这次没人帮他,同学们都乐于助人,一定很愿意帮助悟空吧?那我们就一同看一下题。
甲乙两个仓库共存粮500吨,甲仓库存量比乙仓库的3倍多20吨,甲乙两个仓库各存粮多少吨?
分析:数量关系
甲仓+乙仓=500吨;甲仓=乙仓×3+20
解:设乙仓为x吨,则甲仓为(500-x)吨。
500-x=3x+20
500-20=3x+x
4x=480
x=120
500-120=380(吨)
答:甲仓存粮380吨,乙仓存粮120吨。
小结
总结列方程解题的过程
(1)审题、找准等量关系式。
(2)设未知数。
(3)列方程、解方程。
(4)检验、答语。
例题讲解
1、售出“螃蟹冲刺”、“水母跳床”的个数共84个,“水母跳床”的个数是“螃蟹冲刺”的3倍。两种模型各出售多少个?
“螃蟹冲刺”的个数+“水母跳床”的个数=84(个)
解:设“螃蟹冲刺”x个,则“水母跳床”为3x个。
x+3x=84
(3+1)x=84
4x=84
x=84÷4
x=21
x=21
3x=63
3x=63
答:售出“螃蟹冲刺”21个,“水母跳床”63个。
如果把条件“‘螃蟹冲刺’、‘水母跳床’共84个”改为“‘水母跳床’比‘螃蟹冲刺’多42个”,怎样分析数量关系?怎样列方程?
“水母跳床”的个数-“螃蟹冲刺”的个数=42(个)
解:设“螃蟹冲刺”x个,则“水母跳床”为3x个。
3x-x=42
(3-1)x=42
2x=42
x=42÷2
x=21
x=21
3x=63
3x=63
答:售出“螃蟹冲刺”21个,“水母跳床”63个。
2、售出的“海马狂舞”比“章鱼腾空”多60个。“海马狂舞”的个数是“章鱼腾空”的4倍。两种模型各售出多少个?
(1)怎样分析数量关系?
(2)怎样列方程?
(3)怎样检验结果是否正确?
(1)“海马狂舞”的个数-“章鱼腾空”=60个
(2)设“章鱼腾空”x个,则“海马狂舞”为4x个。
4x-x=60
(4-1)x=60
3x=60
x=60÷3
x=20
x=20
4x=80
4x=80
答:售出“章鱼腾空”20个,“海马狂舞”80个。
(3)检验:
把x=20带入方程左边,得到4×20-20=60;右边等于60,左边等于右边,所以x=20是方程的解。
变式练习
1.地球绕太阳一周约365天,比水星绕太阳一周所需时间的5倍少75天。水星绕太阳一周需多少天?
解析:数量关系
地球绕太阳=水星绕太阳×5-75
答案:88天
2.两位邮递员分别骑摩托车和自行车,同时从相距3000米的两地相向而行。
(1)摩托车的速度是800米/分,自行车的速度是200米/分。两个邮递员经过几分钟后相遇?
(2)他们3分钟后相遇。摩托车的速度是800米/分,自行车的速度是多少?
答案:(1)3分钟(2)200米/分
31.列方程解题(二)
A城动漫公司派代表到B城参加水灵动漫展。A,B两城火车站相距300千米,公司代表乘时速80千米的列车,3小时后,离B城火车站还有60千米。你能提出哪些数学问题?
知识回顾
1.根据问题分别写出两个代数式。
(1)已经行驶的路程是多少?________
________
(2)剩下的路程是多少?_________
_________
(3)两个车站间的路程是多少?________
________
2.根据上面的条件可以列出哪几组等量关系?
(1)以“已经行驶的路程”为等量。
已经行驶的路程=全程-剩下的路程
_____________=_________________
(2)以“剩下的路程”为等量。
剩下的路程=全程-已经行驶的路程
__________=______________
(3)以“两个车站间的距离”为等量。
全程=已经行驶的路程+剩下的路程
___________=_______________
答案:1(1)3×80
300-60
(2)60
300-3×80
(3)300
3×80+60
2(1)3×80
300-60
(2)60
300-3×80
(3)300
3×80+60
例题讲解
1、一列火车从A城到相距300千米的B城,行驶3小时后还剩60千米,这列火车行驶的速度是多少?
解:设这列火车的速度是x千米/时。
(1)3x+60=300
(2)300-3x=60
(3)3x=300-60
(4)(300-60)÷x=3
说一说上面这些方程分别以什么为等量。
解:(1)以“两个车站间的距离”为等量。已经行驶的路程+剩下的路程=全程
(2)以“剩下的路程”为等量。全程-已经行驶的路程=剩下的路程
(3)以“已经行驶的路程”为等量。已经行驶的路程=全程-剩下的路程
(4)以“目前行驶的时间为等量”。(总路程-剩余的路程)÷形式的速度=目前行驶的时间
2、一列火车从A城到相距300千米的B城,行驶速度是80千米/时。行驶几小时后离B城还有60千米?
以什么为等量方程?
解:设行驶x小时后离B城还有60千米。
以“总路程”为等量列方程。
总路程=行驶路程+剩余路程
300=80x+60
课后小作业,想一想有没有其他的等量方程?
答案:1、(1)以“4次运送的水泥”为等量。
4×15
(2)以“每次运送的水泥”为等量。(72-x)÷4
(3)以“需要的水泥总数”为等量。
4×15+x
2、解:设第一天做了x套。
x+30=15×8
x=90
答:第一天做了90套。
3、解:平均每小时修补x本。
6x+400=820
x=70
答:平均每小时修补70本。
变式练习
1、工地需要水泥72吨,每次运15吨。运4次后还差多少吨?
解:设运4次后还差x吨。
把方程补充完整,并说一说分别以什么为等量。
(1)72-x=________(2)15=__________
(3)_________=72
2、服装厂第二天比第一天多做衣服30套,第二天的工作效率是15套/时,工作8小时。第一天做了多少?
3、图书馆要修补820本图书,已经修补了400本。剩下的6小时修补完,平均每小时修补多少本?
32.综合与实践
a×10=50
a
=5
9×b-7×b=10
b
=5
思考一下,下面的字母都代表了什么?
知识回顾
102÷c=2
20×x+40=100
c
=51
x
=3
15×m-7m=56
m
=7
在数学中,人们常用字母表示数,来简明地表达出各个量之间的关系,更好地帮助我们理解。
(一)、用字母表示数的意义
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
(二)、方程的解与解方程
建议:
1.
用方程解决以下问题比较简便:
类型一:和倍、差倍的应用题。
类型二:比谁的几倍多(少)几。
类型三:甲数比乙数多(少)几分之几或百分之几。
2.行程中的相遇问题、相距问题时,求相遇时间或一个车的速度时
,用方程。
……
(三)、列方程解应用题
动漫城有A、B两幢居明楼,A楼有60户居民,B楼有40户居民,两幢楼相距400米。若在两幢楼之间建造一个分类垃圾站,这个垃圾站建在哪里比较合理?
如果垃圾站建造在两幢楼之间,所有的居民到垃圾站的距离之和为:60×200+40×200=20000(米)。
设垃圾站距离楼x米。当x去不同的数值时,两幢楼所有居民到垃圾站的距离之和如下:
x
0
100
200
300
400
距离之和/m
16000
18000
(1)你发现了什么规律?
当x每增加100米,距离之和增加2000米。
(2)如果两幢楼的居民数相等,垃圾站设置在哪里比较合理?
两幢楼之间。
解:
(3)如果要让两幢楼的居民到垃圾站的距离和相等,垃圾站设置在哪里比较合理?
由题意得,可列方程:
60×x=40×(400-x)
答:建造在距离A楼160处较合理。
x=160
100x=16000
(1)分析题意。认真读题,反复审题,弄清问题中的已知量是什么,未知量是什么,它们
之间有什么等量关系;
?
(2)设未知数为x。合理选择未知数是解题的关键步骤之一。一般设题目里所求的未知数
是x,特殊情况下也可设与所求量相关的另一个未知数为x;
?
列方程解应用题的一般步骤:
三、课堂小结:
(3)列方程。根据所设的未知量x和题目中的已知条件,利用等量关系列出方程;
(4)解方程。求未知数x的值;
?
(5)检验并答题。对方程的解进行检查验算,看是否符合题意,针对问题作出答案。
1、果园里有苹果树78棵,比梨树的3倍多6棵,比李子树的4倍少10棵。
(1)果园里有梨树多少棵?
(2)果园里有李子树多少棵?
四、延伸拓展:
解:设果园里有梨树x棵,李子树有y棵。
3x
+
6
=
78
3x
=
78
-
6
x
=
72
÷
3
x
=
24
答:果园里有梨树24棵,李子树有22树。
2.
一块三角形地的面积是780平方米。它的
高是30米,底边是多少米?
解:设底边为x米。
0.5
×
30x
=
780
30x
=
780
÷
0.5
x
=
1560
÷
30
x
=
52
答:底边长为52米。
谢
谢
五
代数式与方程
复习课件
用字母表示数
简易方程
列方程解应用题
用字母表示数的意义
方程的解
将数值代入式子求值
解方程
列方程解应用题的一般步骤
方程解应用题
知识网络
25.代数式一
在教学中,人们常用字母表示数。想一想,下面的字母分别表示多少?
a×3=27
a=9
=9
5×x+40
=
100
15b-7×b=96
b=12
c=8
x=12
像
a×3,
,
15×b-7×b,5x+40这样含有字母的式子叫代数式。单独一个数或字母也是代数式。
在代数式里,数字和字母、字母和字母相乘时,乘号可以写成“ ”,或省略不写,通常数字写在字母前面。
写做
a.3或3a
.
如:
15×b-7×b
写做15b-7b
x
5×
写做5
x
a×3
1与任何字母相乘时,1可以省略不写。
例如:1×a
可以直接写成a
m×5
可以直接写成5m
练一练
1.如果大螃蟹爬行的速度是a厘米/分,小螃蟹爬行的速度是b厘米/分,它们都爬了5分钟,那么,
(1)大螃蟹爬了多少路径?
(1)大螃蟹爬了5a厘米。
(2)小螃蟹爬了多少路径?
(2)小螃蟹爬了5b厘米。
(3)大螃蟹比小螃蟹多爬了多少路径?
(3)大螃蟹比小螃蟹多爬了(5a-5b)厘米。
(4)一辆公共汽车上原来有x人,到新街口车站下去5人,又上来y人。现在车上有(
)人。
(1)储蓄罐里原来有n元,今天小刚又存入3元,储蓄罐里现在有(
)元。
(2)一件上衣a元,一条裤子比上衣便宜
12元,一条裤子(
)元。
(3)小刚每天看课外书15页,a天共看了(
)页。
n+3
a-12
15a
x-5
+y
练一练
例2.章鱼的个数与腿的条数之间的关系。
章鱼个数
1
2
4
...
n
腿的条数
8
16
24
40
...
(1)完成上表。
章鱼的个数是n时,腿的条数是8n。
当n=15时,8n=8×15=12。代数式8n的值是120。
(2)想一想,n=15,8n=120分别表示什么意思?
(2)n=15表示章鱼的个数是15,8n=120分别表示章鱼的腿
数是120。
3
5
32
8n
巩固练习1:
有n只帆船,每只帆船乘坐a条海马,码头上还有m条海马。有代数式an+m表示海马的总条数。如果a=5,n=7,m=12,写成代数式的值。
解:把a=5,n=7,m=12带入代数式an+m,
得,an
+
m=5×7
+
12=35
+
12=47
爸爸比小明大30岁,爸爸今年n岁,5年后小明几岁?
5年后(5n-30)岁
巩固练习2:
26.代数式二
根据运算定律把下面的图形算式化简:
8×
+5×
3a-2a
8a+5a
=(8+5)×
=13×
=(3-2)a
=a
=(8+5)a
=13a
根据运算定律可以把图形式化简,同样也可以把代数式化简。
例1.螃蟹爬行的速度是a厘米/分,第一次爬行20分钟,第二次爬行30分钟。第二次比第一次多爬行多少厘米?
30a-20a=(30-20)a
=10a
第一次
第二次比第一次多爬行多少厘米?
第二次
随堂练习:
1.化简下列各式。
24b-9b
5x+3x-7
12b+4b+9b
6x-3x+5
=(24-9)b
=15b
=(5+3)x-7
=8x-7
=(12+4+9)b
=25b
=(6-3)x+5
=3x+5
1.写出下面数量关系的代数式,能化简的要化简。
(1)某宾馆某月每天烧煤x千克,4天烧煤都是千克?该月一共烧23天,还要烧煤多少千克?
(2)此宾馆有2人间(2个床位)客房a间,3人间客房b间。一共有多少个床位?
(1)4a千克
(1)19a千克
(2)(2a+3b)个
随堂练习:
巩固练习:化简下面各题。
1.2x+3x-2
=(2+3)x-2
=5x-2
2.m+2m-m
=(1+2-1)m
=2m
3.9x-4x+2x
=(9-4+2)x
=7x
26a+7a-8
=(26+7)a-8
=33a-8
例2.用代数式表示下图中大长方形的面积。(单位:厘米)
1
2
9
a
4
9a+4a=
a
13
长方形的面积是:
长方形的面积是:
9a
4a
(1)一辆汽车从甲开往乙地,速度是x米/分,先行15分钟,中途休息后再行b分钟,离乙地还有150米。
15分钟
行驶的路程
b分钟
行驶的路程
150米
甲
乙
用代数式表示甲、乙两地的路程。
15x+bx+150=(15x+150)米
x米/分钟
随堂练习:
(2)一辆汽车和一辆货车同时从甲乙两地相对开出。汽车的速度是x米/分,货车的速度是y米/分。20分钟后相遇。
用代数式表示相遇时汽车比货车多行的路程。
20x-20y=20(x-y)米
(3)某学校定制一批服装。服装公司用a=10+2n计算一件服装的成本。a表示成本,n表示做一件服装需要的小时数,计算n=2时的成本。(单位:元)
把n=2代入a=10+2n
得:
c=10+2×2
c=14
随堂练习:
(4)A,B两地相距500米,甲车从A地出发已经行a米,剩下的路程如果每分钟行b米,15分钟可到达。
A
500m
am
15bm
B
分别写出两个表示A,B路程的代数式。
分别写出两个表示剩下路程的代数式。
500m
(a+15b)m
15bm
(500-a)m
5.某工厂制作一批课桌,计划x天完成,实际每天制作23个,提前y天完成任务。
(1)写出x-y表示的意义。
(2)用代数式表示这批竹筐的个数。
(3)当x=10,y=2时,求各代数式的值。
(1)x-y表示实际完成任务用的天数。
(2)23(x-y)个。
(3)x-y=10-2=8
(2)23(x-y)
=23×(10-2)
=184
随堂练习:
(1)我国青少年(7~17岁)在1980年平均身高x厘米,到2000年平均身高增长6cm,2000年我国青少年平均身高________厘米。
(2)人的身高可能会相差2cm,在早上最高,晚上最矮。一个人早上身高
b
厘米,晚上身高可能是________厘米。
(3)鸟的骨骼约是体重的0.05~0.06倍,人的骨骼约是体重的0.18倍,一个人重a千克,骨骼约是________千克。
(4)小英家本月的用电量是80千瓦时,交电费c元,那么电费每千瓦时是________元。
x+6
b-2
0.18a
C÷80
拓展练习:
27.认识方程
等式有什么特征?能说说什么样的式子叫做等式吗?
左右两边相等的式子叫做等式。
像2x
=
16,7×2+8=y+8,a+7=9+6这样含有未知数的等式是方程。
讨论:等式与方程有什么关系?
等式
方程
所有的( )都是(
)
有的(
)是(
)
1、试一试:看图列方程
2x=500
12+x=20
500g
2、分别写出两个等式、两个方程,同桌交换检查并更正。
3、看图列方程
x+50=100
5x=50
50g
100g
50g
4、看图列方程。
海马条数:
海马条数:
a
2a
24
a+2a=24
4x=16.8
200+x=450
28.等式的性质
等式有什么特征?能说说什么样的式子叫做等式吗?
左右两边相等的式子叫做等式。
b
a
天平与等式
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
等式的左边
等式的右边
等号
用字母a表示一个
的质量,每个
都重一个单位,右图用等式表示为a=3。
a
=
3
1.从天平左侧和右侧的托盘里分别放进或取出2
个
,你还能用等式表示吗?
a=3
a+2=3+2
a=3
a+2-2=3+2-2
(1)如果天平两侧分别放进或取出5个
、8个
……呢?
a+5=3+5
天平两侧分别放进或取出8个
a+5-5=3+5-5
天平两侧分别放进或取出5个
a+8=3+8
a+8-8=3+8-8
(2)如果用字母b表示一个的
质量,那么a=3b。等式两边都加上2b,怎样表示呢?
a+2b=3b+2b
等式两边都加上或减去同一个数或式,所得的结果仍为等式。这就是等式的性质。
练一练:
1、在
里填数。
35+48=60+23
+48
=+23
42+a=37+b
+a=
+b
+5
+5
-12
-12
40
65
30
25
5a-4=3a+12
2a-0=
0+
+4
-3a
-3a
+4
14
7b+9
=9b
-5
0+
=
-5
-7b
+5
-7b
+5
16
2b
练一练:
1、在
里填数。
联系等式:(1)a+30=c+50
你能变出几个等式?
巩固练习:
a-50-c=30
a-c=50-30
a+30-c=50
(2)判断:已知a=b,c=d
a-2=b-3
(
)
a+c=b+d
(
)
a-b=c-
d
(
)
a+5=c+5
(
)
对
错
对
对
例2.观察天平左侧和右侧的变化,你发现了什么?
a=3
a×2=3×2
a=3
a×2÷2=3×2÷2
从左侧到右侧,天平的左右两侧都扩大2倍,天平仍然平衡。
从右侧到左侧,天平的左右两侧都缩小3倍,天平仍然平衡。
讨论:如果天平两侧都乘或处以3,4,5…,b呢?
等式的两边都乘或除以同一个不为0的数或式,所得的结果仍为等式。这也是等式的性质。
练一练:
1、在
里填数。
3a=5b
15a=
b
8(x+5)=96
(x+5)=
×5
÷8
÷8
×5
25
1
12
2a=3b
a=
b
20(x+3)=60
(x+3)=
×4
÷20
÷20
×4
12
1
3
8
练一练:
1、在
里填数。
3.x÷4=48
x÷4
○(
)
=48
○(
)
4.x
×
4=48
x
×
4
○(
)
=48
○(
)
2.x-4=48
x-4
○
(
)
=48
○
(
)
1.x+4=48
x+4
○
(
)
=48○(
)
在○里填上合适的运算符号,在(
)里填上合适的数。
+
+
15
15
-
15
15
-
÷
4
÷
4
÷
4
4
÷
29.解方程
例1.买某种布料5米,共用去80元。这种布料每米多少元?
如果用
表示这种布料的单价,你能列出图形等式吗?
5×
=80
5×
=80
如果用过x代替
,这个图形算式可以怎么写?
你能求x的值吗?
5x=80
5x=80
解:5x=80
x=80÷5
x=16
等式两边都除以5.
积除以一个因数
使方程左右两边相等的未知数的值叫做方程的解。
检验:把x=16带入方程左边,5×16=80,与方程右边相等,所以x=16使方程的解。
求方程解的过程叫做解方程
练一练1.直接说出x的值。
35+x=100
x÷6=25
21x=63
x-3.5=5.8
42÷x=7
2.5-x=2.5
x=65
x=130
x=3
x=9.3
x
=6
x=0
1.请你画图或举例说说下面这句话的意思:
等式两边都加上(或减去)同一个数,等式仍然成立。
2.看图列方程,并解方程。
y+20=50+20+10
解:y+20=80
y=
80-20
y=60
3.
解方程。
x-9=12
解:x=12+9
x=21
x-12.3=3.8
解:x=3.8+12.3
x=16.1
4.
看图列方程,并解方程。
x+4=19
解:x=19-4
x=15
x-62=486
解:x=486+62
x=548
y+60+50=180
解:y+110=180
y=70
内装x个
19个
原价:x元
降价:62元
现价:486元
60°
50°
y°
1.解方程:18(x+14)=540
解:18(x+14)=540
等式两边都除以18
等式两边都减14
积除以一个因数
和减去一个加数
检验:18×(16+14)=540
x+14=540÷18
x=30-14
x=16
练一练
2.解方程。
2x-5=79
解:2x=79+5
2x=84
x=84÷2
x=42
420-3y=120
解:3y=420-120
3y=300
y=300÷3
y=100
6(43+x)=330
解:43+x=330÷6
43+x=55
x=55-43
x=12
16y=12(y+6)
解:16y=12y+72
6y-12y=72
4y=72
y=18
3.花圃里有铁树、君子兰和腊梅花共260盆。腊梅花的盆数是君子兰的2倍,君子兰的盆数是铁树的3倍。
铁树
君子兰
腊梅花
260盆
1份
3份
(3×2)份
x盆
3x盆
(2×3)x盆
x+3x+(3×2)x=260
解:10x=260
x=26
1.看图列方程,并解方程。
(1)
(2)
18a
20y
24y-20=20y
解:24y-20y=20
4y=20
y=5
15(a+4)
15(a+4)=18a
解:15a+60=18a
18a-15a=60
3a=60
a=20
巩固练习
1.
看图回答问题。
⑴图中哪一段长度是(200-
)米?
⑵图中哪一段长度是(200+
)米?
⑶根据上图,你能列出两个不同的方程吗?
150米
500米
150+
x
=200
150+x+y=500
拓展应用
30.列方程解题(一)
知识回顾
最近悟空有些闷闷不乐,想必是遇到了什么难题,我用千里眼看一下,原来是遇到了一道数学题,可是这次没人帮他,同学们都乐于助人,一定很愿意帮助悟空吧?那我们就一同看一下题。
甲乙两个仓库共存粮500吨,甲仓库存量比乙仓库的3倍多20吨,甲乙两个仓库各存粮多少吨?
分析:数量关系
甲仓+乙仓=500吨;甲仓=乙仓×3+20
解:设乙仓为x吨,则甲仓为(500-x)吨。
500-x=3x+20
500-20=3x+x
4x=480
x=120
500-120=380(吨)
答:甲仓存粮380吨,乙仓存粮120吨。
小结
总结列方程解题的过程
(1)审题、找准等量关系式。
(2)设未知数。
(3)列方程、解方程。
(4)检验、答语。
例题讲解
1、售出“螃蟹冲刺”、“水母跳床”的个数共84个,“水母跳床”的个数是“螃蟹冲刺”的3倍。两种模型各出售多少个?
“螃蟹冲刺”的个数+“水母跳床”的个数=84(个)
解:设“螃蟹冲刺”x个,则“水母跳床”为3x个。
x+3x=84
(3+1)x=84
4x=84
x=84÷4
x=21
x=21
3x=63
3x=63
答:售出“螃蟹冲刺”21个,“水母跳床”63个。
如果把条件“‘螃蟹冲刺’、‘水母跳床’共84个”改为“‘水母跳床’比‘螃蟹冲刺’多42个”,怎样分析数量关系?怎样列方程?
“水母跳床”的个数-“螃蟹冲刺”的个数=42(个)
解:设“螃蟹冲刺”x个,则“水母跳床”为3x个。
3x-x=42
(3-1)x=42
2x=42
x=42÷2
x=21
x=21
3x=63
3x=63
答:售出“螃蟹冲刺”21个,“水母跳床”63个。
2、售出的“海马狂舞”比“章鱼腾空”多60个。“海马狂舞”的个数是“章鱼腾空”的4倍。两种模型各售出多少个?
(1)怎样分析数量关系?
(2)怎样列方程?
(3)怎样检验结果是否正确?
(1)“海马狂舞”的个数-“章鱼腾空”=60个
(2)设“章鱼腾空”x个,则“海马狂舞”为4x个。
4x-x=60
(4-1)x=60
3x=60
x=60÷3
x=20
x=20
4x=80
4x=80
答:售出“章鱼腾空”20个,“海马狂舞”80个。
(3)检验:
把x=20带入方程左边,得到4×20-20=60;右边等于60,左边等于右边,所以x=20是方程的解。
变式练习
1.地球绕太阳一周约365天,比水星绕太阳一周所需时间的5倍少75天。水星绕太阳一周需多少天?
解析:数量关系
地球绕太阳=水星绕太阳×5-75
答案:88天
2.两位邮递员分别骑摩托车和自行车,同时从相距3000米的两地相向而行。
(1)摩托车的速度是800米/分,自行车的速度是200米/分。两个邮递员经过几分钟后相遇?
(2)他们3分钟后相遇。摩托车的速度是800米/分,自行车的速度是多少?
答案:(1)3分钟(2)200米/分
31.列方程解题(二)
A城动漫公司派代表到B城参加水灵动漫展。A,B两城火车站相距300千米,公司代表乘时速80千米的列车,3小时后,离B城火车站还有60千米。你能提出哪些数学问题?
知识回顾
1.根据问题分别写出两个代数式。
(1)已经行驶的路程是多少?________
________
(2)剩下的路程是多少?_________
_________
(3)两个车站间的路程是多少?________
________
2.根据上面的条件可以列出哪几组等量关系?
(1)以“已经行驶的路程”为等量。
已经行驶的路程=全程-剩下的路程
_____________=_________________
(2)以“剩下的路程”为等量。
剩下的路程=全程-已经行驶的路程
__________=______________
(3)以“两个车站间的距离”为等量。
全程=已经行驶的路程+剩下的路程
___________=_______________
答案:1(1)3×80
300-60
(2)60
300-3×80
(3)300
3×80+60
2(1)3×80
300-60
(2)60
300-3×80
(3)300
3×80+60
例题讲解
1、一列火车从A城到相距300千米的B城,行驶3小时后还剩60千米,这列火车行驶的速度是多少?
解:设这列火车的速度是x千米/时。
(1)3x+60=300
(2)300-3x=60
(3)3x=300-60
(4)(300-60)÷x=3
说一说上面这些方程分别以什么为等量。
解:(1)以“两个车站间的距离”为等量。已经行驶的路程+剩下的路程=全程
(2)以“剩下的路程”为等量。全程-已经行驶的路程=剩下的路程
(3)以“已经行驶的路程”为等量。已经行驶的路程=全程-剩下的路程
(4)以“目前行驶的时间为等量”。(总路程-剩余的路程)÷形式的速度=目前行驶的时间
2、一列火车从A城到相距300千米的B城,行驶速度是80千米/时。行驶几小时后离B城还有60千米?
以什么为等量方程?
解:设行驶x小时后离B城还有60千米。
以“总路程”为等量列方程。
总路程=行驶路程+剩余路程
300=80x+60
课后小作业,想一想有没有其他的等量方程?
答案:1、(1)以“4次运送的水泥”为等量。
4×15
(2)以“每次运送的水泥”为等量。(72-x)÷4
(3)以“需要的水泥总数”为等量。
4×15+x
2、解:设第一天做了x套。
x+30=15×8
x=90
答:第一天做了90套。
3、解:平均每小时修补x本。
6x+400=820
x=70
答:平均每小时修补70本。
变式练习
1、工地需要水泥72吨,每次运15吨。运4次后还差多少吨?
解:设运4次后还差x吨。
把方程补充完整,并说一说分别以什么为等量。
(1)72-x=________(2)15=__________
(3)_________=72
2、服装厂第二天比第一天多做衣服30套,第二天的工作效率是15套/时,工作8小时。第一天做了多少?
3、图书馆要修补820本图书,已经修补了400本。剩下的6小时修补完,平均每小时修补多少本?
32.综合与实践
a×10=50
a
=5
9×b-7×b=10
b
=5
思考一下,下面的字母都代表了什么?
知识回顾
102÷c=2
20×x+40=100
c
=51
x
=3
15×m-7m=56
m
=7
在数学中,人们常用字母表示数,来简明地表达出各个量之间的关系,更好地帮助我们理解。
(一)、用字母表示数的意义
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
(二)、方程的解与解方程
建议:
1.
用方程解决以下问题比较简便:
类型一:和倍、差倍的应用题。
类型二:比谁的几倍多(少)几。
类型三:甲数比乙数多(少)几分之几或百分之几。
2.行程中的相遇问题、相距问题时,求相遇时间或一个车的速度时
,用方程。
……
(三)、列方程解应用题
动漫城有A、B两幢居明楼,A楼有60户居民,B楼有40户居民,两幢楼相距400米。若在两幢楼之间建造一个分类垃圾站,这个垃圾站建在哪里比较合理?
如果垃圾站建造在两幢楼之间,所有的居民到垃圾站的距离之和为:60×200+40×200=20000(米)。
设垃圾站距离楼x米。当x去不同的数值时,两幢楼所有居民到垃圾站的距离之和如下:
x
0
100
200
300
400
距离之和/m
16000
18000
(1)你发现了什么规律?
当x每增加100米,距离之和增加2000米。
(2)如果两幢楼的居民数相等,垃圾站设置在哪里比较合理?
两幢楼之间。
解:
(3)如果要让两幢楼的居民到垃圾站的距离和相等,垃圾站设置在哪里比较合理?
由题意得,可列方程:
60×x=40×(400-x)
答:建造在距离A楼160处较合理。
x=160
100x=16000
(1)分析题意。认真读题,反复审题,弄清问题中的已知量是什么,未知量是什么,它们
之间有什么等量关系;
?
(2)设未知数为x。合理选择未知数是解题的关键步骤之一。一般设题目里所求的未知数
是x,特殊情况下也可设与所求量相关的另一个未知数为x;
?
列方程解应用题的一般步骤:
三、课堂小结:
(3)列方程。根据所设的未知量x和题目中的已知条件,利用等量关系列出方程;
(4)解方程。求未知数x的值;
?
(5)检验并答题。对方程的解进行检查验算,看是否符合题意,针对问题作出答案。
1、果园里有苹果树78棵,比梨树的3倍多6棵,比李子树的4倍少10棵。
(1)果园里有梨树多少棵?
(2)果园里有李子树多少棵?
四、延伸拓展:
解:设果园里有梨树x棵,李子树有y棵。
3x
+
6
=
78
3x
=
78
-
6
x
=
72
÷
3
x
=
24
答:果园里有梨树24棵,李子树有22树。
2.
一块三角形地的面积是780平方米。它的
高是30米,底边是多少米?
解:设底边为x米。
0.5
×
30x
=
780
30x
=
780
÷
0.5
x
=
1560
÷
30
x
=
52
答:底边长为52米。
谢
谢
同课章节目录
- 一 自然数与整数
- 1.自然数
- 2.认识负数
- 3.整除
- 4.能被2,5整除的数
- 5.能被3整除的数
- 6.倍数与因数
- 7.素数与合数
- 8.分解因数
- 二 可能性
- 9.认识可能性
- 三 分数与除法
- 10.分数与除法的关系
- 11.一个数是另一个数的几分之几
- 12.真分数与假分数
- 13.假分数与整数
- 14.假分数与带分数
- 四 几何小天地
- 15.角的度量
- 16.角的分类
- 17.轴对称图形
- 18.图形的旋转
- 19.三角形的边
- 20.三角形的角
- 21.三角形内角和
- 22.平行四边形的边与角
- 23.梯形的边与角
- 24.图形的高与底
- 五 代数式与方程
- 25.代数式(一)
- 26.代数式(二)
- 27.认识方程
- 28.等式的性质
- 29.解方程
- 30.列方程解题(一)
- 31.列方程解题(二)
- 六 总复习
