四年级下册数学课件-一 自然数与整数 复习课件 浙教版 (共100张PPT)
文档属性
| 名称 | 四年级下册数学课件-一 自然数与整数 复习课件 浙教版 (共100张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 00:00:00 | ||
图片预览








文档简介
(共100张PPT)
一
自然数与整数
复习课件
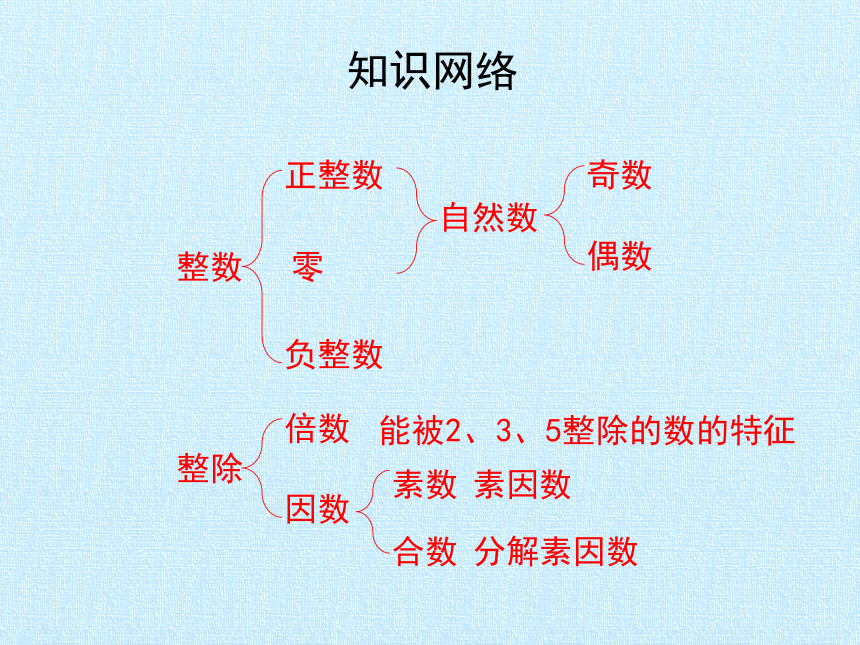
知识网络
整数
整除
正整数
零
负整数
自然数
奇数
偶数
倍数
因数
能被2、3、5整除的数的特征
素数
合数
素因数
分解素因数
1.自然数
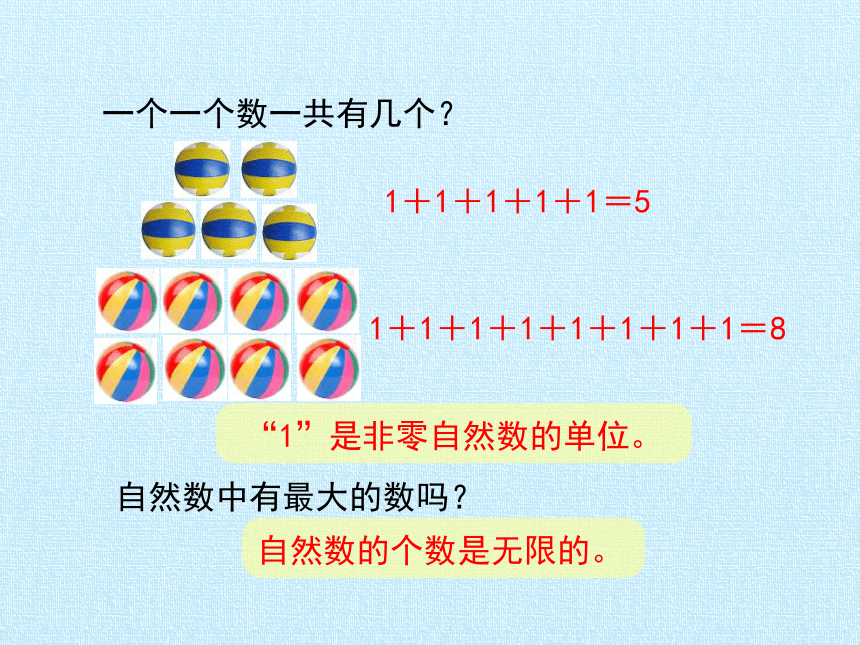
1.数一数下面体育用品的个数。
人们在数物体时,用来表示物体个数的1,2,3,4,5,6,7,8,……以及0叫做自然数。
知识回顾
自然数中有最大的数吗?
1+1+1+1+1=5
1+1+1+1+1+1+1+1=8
一个一个数一共有几个?
“1”是非零自然数的单位。
自然数的个数是无限的。
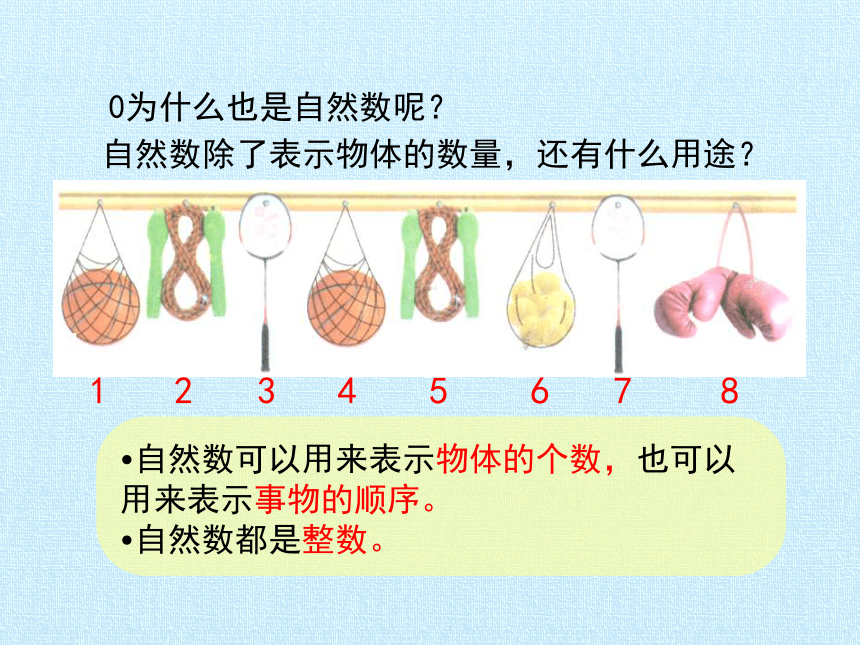
0为什么也是自然数呢?
自然数除了表示物体的数量,还有什么用途?
1
2
3
4
5
6
7
8
自然数可以用来表示物体的个数,也可以用来表示事物的顺序。
自然数都是整数。
2.说一说,下面的数中,哪些表示顺序?哪些表示个数?
(1)强强家的门牌是132号,聪聪家所在的小区有132户人家。
(2)60个同学排成4列,迪迪排在第3列第12个。
用来表示门牌的次序。
表示小区人家的户数多少。
表示学生的人数。
表示学生队列的个数。
表示迪迪所在列的序号。
表示迪迪位置的序号。
门牌号132号的132表示顺序。
132户人家的132表示个数。
60个同学和4列中的60和4表示个数。
第3列和第12个中的3和12表示顺序。
1、(1)把自然数从小到大排列,999前面的一个数是(
),999后面的一个数是(
)。
(2)796后面的连续五个自然数是
(
)。
998
1000
797、798、799、800、801
练习
2
.把自然数1至200按下面的方法组成A,B,C三组。
想一想:这些数的排列方法是怎样的?A组的数有什么特点?B组、C组的数呢?
大家讨论:
(1)每一组有多少个数?最后一个数各是什么?
(2)B组第7个数是多少?C组第56个数呢?
(3)173是哪一组的第几个数?
A组:1
6
7
12
13
18
……
B组:2
5
8
11
14
17
……
C组:3
4
9
10
15
16
……
2.认识负数
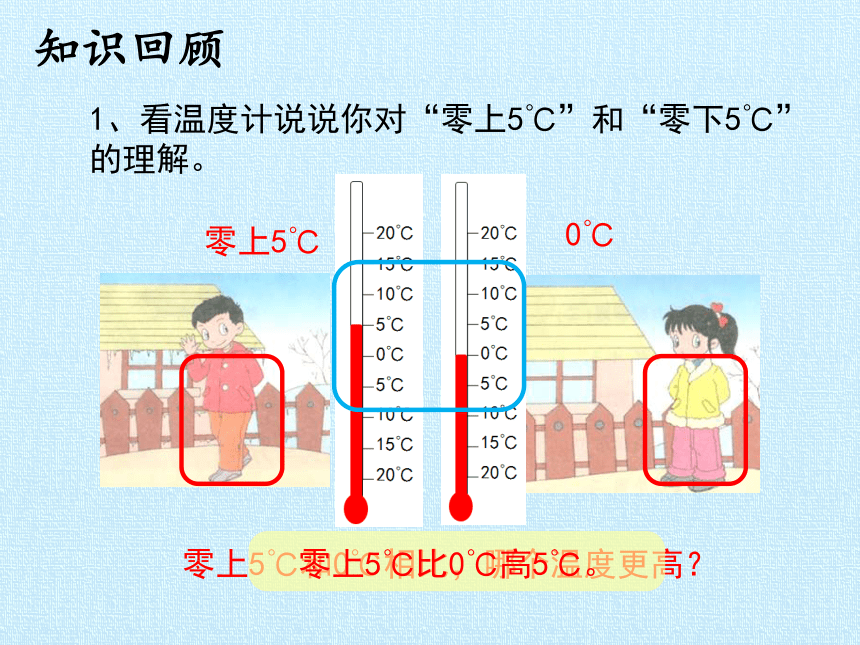
1、看温度计说说你对“零上5℃”和“零下5℃”的理解。
零上5℃
0℃
零上5℃和0℃相比,哪个温度更高?
零上5℃比0℃高5℃。
知识回顾
1、看温度计说说你对“零上5℃”和“零下5℃”的理解。
0℃
零下5℃
0℃和零下5℃相比,哪个温度更高?
零下5℃比0℃低5℃。
零上5℃比0℃高5℃。
零下5℃比0℃低5℃。
“零上温度”和“零下温度”是具有相反意义的量。
看温度是在零上还是在零下,要以什么作标准?
以0℃做标准,比0℃高的是零上温度,比0℃低的是零下温度。
2、迪迪从校门口向东走了3米,强强从校门口向西走了3米,看看他们在什么位置。
迪迪
●
强强
●
“向东路程”和“向西路程”是具有相反意义的量。
它们有什么相同点?
两种具有相反意义的量。
为了表示具有相反意义的量,我们把一种意义的量规定为正,用如:3、5等数来表示,这样的数是正数。正数前面也可以写上“+”(正号)。
把另一种意义相反的量规定为负,在数的前面写上“-”(负号)来表示。如-3、-5等,这样的数是负数。
读作:负三
读作:正三
0既不是正数也不是负数。
3、生活中还有哪些量可以用正数与负数表示?
1.在知识竞赛中,如果把加10分记为+10分,那么扣20分记为(
)。
2.汽车在一条南北走向的公路上行驶,如果规定向北行驶的路程为正,那么汽车向北行驶60千米,记为(
)千米,汽车向南行驶80千米,记为(
)千米。
-20
+60
-80
练习
3.某仓库把运进大米吨数记为正,则-4吨表示(
),+6吨表示(
)。
4.如果+5表示转盘向逆时针方向转5圈,那么-3表示(
)。
运出4吨
运进6吨
顺时针方向转3圈
3.整除
商是整数而没有余数,我们可以说:
6能被3整除,也能被2整除。
……
知识回顾
商是整数而有余数,我们可以说:
6不能被4整除。
……
整数a除以整数b(b≠0),所得的商是整数,余数是0,就说a能被b整除。
1、被除数和除数都是整数。
2、商是整数。
3、商后没有余数。
第一个数能被第二个数整除需要满足什么条件?
1、240÷60=6,(
)能被(
)整除。
240
60
2、在36,9,4,12这几个数中,选择两个说一说它们的整除关系。
36能被9整除。
36能被4整除。
12能被4整除。
36能被12整除。
练习
3、15能被哪些数整除?你能用15个小正方形拼成的长方体来表示吗?
15能被1、3、5、15整除。
4、看图说一说什么数能被什么数整除,什么数不能被什么数整除。
18不能被4整除。
18不能被5整除。
14不能被3整除。
5、看图说一说什么数能被什么数整除,什么数不能被什么数整除。
7能被7整除。
7能被1整除。
18能被6整除。
18能被3整除。
4.能被2、5整除的数
1、在1~50的自然数中,分别找出能被4和6整除的数。
被4整除
被6整除
4
8
12
16
20
24
28
32
36
40
44
48
6
12
18
24
36
42
48
知识回顾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
在1~100的自然数中,找出能被5整除的数,用红笔圈出来;找出能被2整除的数,用紫笔圈出来。
能被2整除的数有什么特征?
能被2整除的数的特征:个位上是0、2、4、6、8。
一个正整数,如果能被2整除,这个数叫做偶数;如果不能被2整除,这个数叫做奇(jī)数。
最小的奇数是1,最小的偶数是0。
你知道吗?
能被5整除的数有什么特征?
能被5整除的数的特征:个位上是0或5。
1、能被2整除的数的特征:
2、能被5整除的数的特征:
整数
正整数
零
负整数
自然数
奇数
偶数
最小的奇数是1,最小的偶数是0。
个位上是0、2、4、6、8的数
个位上是0或5的数
1.下面哪些数能被2整除?为什么?
18
27
30
85
423
76
314
个位上是0、2、4、6、8的数能被2整除。
练习
2.下面哪些数能被5整除?为什么?
30
76
85
370
553
1310
504
个位上是0或5的数能被5整除。
3.把下列各数分别按要求填在相应的圈内。
76
83
293
438
199
2054
977
奇数
偶数
83、293、199、
977、
76、438、2054
4.同时能被2和5整除的数有什么特征?举例说明。
个位上是0、2、4、6、8的数能被2整除。
个位上是0或5的数能被5整除。
个位上是0数能被2和5整除。
10、20、30、40、50、60、70、……
5.用0,1,5这三个数字组成的三位数。
(1)能被2整除的数有(
)。
(2)能被5整除的数有(
)。
(3)既能被2整除,又能被5整除的数有
(
)。
150、510
105、150、510
150、510
5.能被3整除的数
在下面的数中分别找出能被2和5整除的数。
被2整除的数
被5整除的数
18
24
30
36
40
42
46
50
80
100
25
30
40
45
50
65
80
100
35
18
24
25
30
35
36
40
42
45
46
50
65
80
100
能被3整除的数有什么特征?
知识回顾
1、根据数位表中的小棒数,完成下表。
摆出的数
用小棒的根数
是否能被3整除
12
3
√
21
3
√
22
4
×
24
36
观察上面的结果,你发现了小棒的根数与能否被3整除有什么关系?
6
9
7
12
57
43
×
√
√
√
2、从10~50自然数中找出能被3整除的数,分别把个位、十位上的数相加,并把和填在下表中。
18
9
21
3
24
6
27
9
30
3
33
6
36
9
39
12
42
6
45
9
48
12
观察个位、十位上的数相加的和,你发现了什么?
一个数各个数位上的数字的和能被3整除,这个数就能被3整除。
1.你报我答。判断报出的数能否被3整除。
48。
是。
73
……
练习
2.在
里填上一个数字,使这个数能被3整除,各有几种填法?
4
2
1
5
2
5
8
1
4
7
0
3
6
9
6.倍数与因数
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
运动会上两个班同学分别排出下面两种队形,算一算两班各有多少人。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9×4=36(人)
5×7=35(人)
知识回顾
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9×4=36(人)
4×9=36(人)
36是9和4的倍数,
9和4是36的因数。
5×7=35(人)
7×5=35(人)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35是5和7的倍数,
5和7是35的因数。
根据算式说一说哪个数是哪个数的倍数,哪个数是哪个数的因数。
25×3=75
20×5=100
在25×3=75中,75是25和3的倍数,25和3是75的因数。
在20×5=100中,100是20和5的倍数,20和5是100的因数。
如果a×b=c(a,b,c是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。
判断:3是因数,18是倍数。(
)
×
3×6=18,我们可以说3是18的因数,18是3的倍数。单独的3和18不能说是因数或倍数。
下面哪些数是7的倍数?与同伴交流你的想法。
7
14
17
25
77
7=7×1
14=7×2
77=7×11
所以7,14,77是7的倍数。
下面哪些数是7的倍数?与同伴交流你的想法。
7÷7=1
14÷7=2
17÷7=2……3
所以7,14,77是7的倍数。
25÷7=3……4
77÷7=11
7
14
17
25
77
7的倍数
1×7=7
7,14,21,28,35,42,49,…都是7的倍数。
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
……
一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
你能找出24的因数吗?
根据乘法算式找出24的因数。
1×24=24
2×12=24
3×8=24
4×6=24
1和24是24的因数
2和12是24的因数
3和8是24的因数
4和6是24的因数
如何根据除法算式找出24的因数?
1×24=24
2×12=24
3×8=24
4×6=24
24÷1=24
24÷2=12
24÷3=8
24÷4=6
24的因数有:
1、2、3、4、6、8、12、24。
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
你能找出24的因数吗?
1.分别找出18和20的所有因数。
18
3
6
2
9
1、2、3、6、9、18。
20
2
10
4
5
1、2、4、
5、10、20。
练习
2.分别找出4和5的倍数。
8
12
16
20
4、8、12、
16、20……
10
15
20
25
5、10、15、
20、25……
7.素数与合数
1.用若干个小正方形拼成长方形的方法,研究3,4,5,6这几个数分别有哪些因数。
3的因数:1,3。
4的因数:1,2,4。
知识回顾
1.用若干个小正方形拼成长方形的方法,研究3,4,5,6这几个数分别有哪些因数。
5的因数:1,
5
6的因数:1,2,3,6
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
1的因数有
2的因数有
3的因数有
4的因数有
5的因数有
6的因数有
1
1,2
1,3
1,2,4
1,5
1,2,3,6
7的因数有
8的因数有
9的因数有
10的因数有
11的因数有
12的因数有
1,7
1,2,4,8
1,3,9
1,2,5,10
1,11
1,2,3,4,6,12
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
只有一个因数
只有1和它本身两个因数
至少有三个因数
1
2,3,5,7,11
4,6,8,9,10,12,
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
一个数如果除了1和它本身,还有别的因数,这样的数叫做合数。
1的因数只有1,1既不是素数,也不是合数。
只有一个因数
只有1和它本身两个因数
至少有三个因数
1
2,3,5,7,11
4,6,8,9,10,12,
一个数,如果只有1和它本身两个因数,这样的数叫做素数(也叫质数)。
1
2,3,5,7,11
4,6,8,9,10,12,
判断下列各数中哪些是素数,哪些是合数。
17
22
29
35
37
87
93
96
素数:17,29,37。
合数:22,35,87,93,96。
找出下表中的素数。
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
把100以内的素数在下表中涂色表示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
把100以内的素数在下表中涂色表示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
(1)观察100以内的数表,素数是怎样分布的?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
除2、3以外,素数大都分布在6的倍数的两边,但6的倍数两边的数不一定都是素数。
(2)在以4或6为首的一列数中,有没有素数?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
没有。以4为首和以6为首的两列数分别是2和3的倍数。
(3)选几个素数,分别除以6,它们的余数有什么特点?
7÷6=1……1
100以内的素数。
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
11÷6=1……5
13÷6=2……1
17÷6=2……5
19÷6=3……1
23÷6=3……5
29÷6=4……5
31÷6=5……1
余数为1或者5。
自然数
因数
自然数
因数
15
32
19
37
21
41
28
45
1.写出下面各数的因数。
1,3,5,15
1,19
1,3,7,21
1,2,4,7,14,28
1,2,4,8,16,32
1,37
1,41
1,3,5,9,15,45
练习
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2.探索。
(1)先划去1,再一次划去2,3,5,7的倍数
(2,3,5,7除外)。
(2)没有划去的数都是素数吗?
是
3.在
里填既是素数,又是奇数的数。
24=
+
8=
+
10=
+
12=
+
22=
+
16=
+
11
13
3
5
3
7
5
7
5
17
5
11
4.把下面的自然数分成两类。
21、29、45、51、73、81、91、97、
(1)素数:(
)。
(2)合数:(
)。
5.按顺序说出20以内的全部素数,看谁说得快。
29、73、97、
21、45、51、81、91
2、3、5、7、11、13、17、19
6.判断。
(1)正整数除了1,不是素数就是合数。(
)
(2)9既是奇数,又是合数。(
)
(3)13的因数都是素数。(
)
7.在两位数的素数中:
(1)个位是1的有(
)
(2)个位是3的有(
)
(3)个位是7的有(
)
(4)个位是9的有(
)
√
√
×
11、31、41、61、71
13、23、43、53、73、83、
17、37、47、67、97
19、29、59、79、89
8.写出5个素数,把它们从小到大排列起来,使相邻两个数的差都是6。
5、11、17、23、29、
8.分解素因数
下面各数中哪些是素数,哪些是合数?分别填入指定的圈里。
素数
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
合数
知识回顾
你能把30写成几个素数相乘的形式吗?
先把30分解成两个数相乘的形式,30分解成5×6。
5是素数,不需要再分解;6是合数,需要再进行分解,6分解成2×3。
30
5
6
2
3
你能把30写成几个素数相乘的形式吗?
还可以把30先分解成2×15或3×10,然后再进行分解。
30
2
15
3
5
30
3
10
2
5
无论怎样分解,30都能分解为2、3、5这3个素数相乘的形式。
你能把30写成几个素数相乘的形式吗?
还可以用短除法进行分解。
把要分解的数30写在短除号里。
用30的因数中的素数去除,一般从最小的素数开始。
30
2
用2去除,2是素数。
直到商是素数为止。
15
5
3
15是3的倍数,用3去除,3是素数。
5是素数,分解结束。
把除数和商写成相乘的形式。
30=2×3×5
你能把30写成几个素数相乘的形式吗?
也可以按如下方式分解:
30
5
6
2
3
30
3
10
2
5
30=2×3×5
30=2×3×5
30
5
6
2
3
30
15
5
3
2
30=2×3×5
30可以写成素数2、3、5相乘的形式,2、3、5叫做30的素因数。
把一个合数写成用素因数相乘的形式表示出来,叫做分解素因数。
你能把30写成几个素数相乘的形式吗?
1、把下面各数分解素因数。
24
35
45
77
84
24=2×2×2×3
35=5×7
45=3×3×5
77=7×11
84=2×2×3×7
练习
2、把36、48、60这三个数分解素因数,并指出这三个数有哪些公有的素因数。
36=2×2×3×3
48=2×2×2×2×3
60=2×2×3×5
公有的是2,2,3
3、写出三组成倍数关系的数,并将它们分解素因数。你发现了什么?
6=2×3
36=2×2×3×3
216=2×2×2×3×3×3
……
整理与应用
一
1、填空。
(1)在1,2,3,6,9,17,24,71,80这些自然数中:
(
)是素数,(
)是合数;
(
)是奇数,(
)是偶数;
(
)既是偶数又是素数,(
)既是奇数又是合数。
(2)因为45能被(
)整除,所以45的因数有(
)。
2,3,17,71
6,9,24,80
1,3,9,17,71
2,6,24,80
2
9
1,3,5,9,15,45
1,3,5,9,15,45
2、填空。
(3)在54、37、20、75、87、95这些数中,2的倍数有(
),3的倍数有(
)5的倍数有(
)。
(4)在算式3×5×7=105中,3,5,7是105的(
)。
(5)规定盈利为正,某公司去年亏损18000元,记为(
)元,今年盈利25000元,记为
(
)元。
素因数
-18000
+25000
54,20,
54,75,87
20,75,95
3、先读一读下面的数,再把它们填入对应的圈内。
-6
+15
0
20
-30
-100
50
正数
负数
+15,20,50
-6,-30,-100
4、先把560分解素因数,再写出两个因数相乘积都是560的式子。
(
)×(
)=(
)×(
)
560=2×2×2×2×5×7
7
80
35
16
5、在横线上填上合适的数。
90×8=
×(8+2)
25×(10+
)=35×10
36×20=24×(
+10)
35×(14+2)=
×14
72
4
20
40
类别
童话
少儿科技
智力游戏
故事
数量/本
57
71
93
105
6、下面各种图书分别能平均分给3个班吗?
童话书、智力游戏书、故事书能平均分给3个班。
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
中间各停靠站上车33人,下车49人,共82人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(1)中间各停靠站上、下车共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
从A站驶向B站时,车上共有36人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(2)从A站驶向B站时,车上共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
从D站驶向E站时,车上共有31人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(3)从D站驶向E站时,车上共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
公交车到达体育馆时,车上还剩多少人?
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(4)你还能提出哪些数学问题?
谢
谢
一
自然数与整数
复习课件
知识网络
整数
整除
正整数
零
负整数
自然数
奇数
偶数
倍数
因数
能被2、3、5整除的数的特征
素数
合数
素因数
分解素因数
1.自然数
1.数一数下面体育用品的个数。
人们在数物体时,用来表示物体个数的1,2,3,4,5,6,7,8,……以及0叫做自然数。
知识回顾
自然数中有最大的数吗?
1+1+1+1+1=5
1+1+1+1+1+1+1+1=8
一个一个数一共有几个?
“1”是非零自然数的单位。
自然数的个数是无限的。
0为什么也是自然数呢?
自然数除了表示物体的数量,还有什么用途?
1
2
3
4
5
6
7
8
自然数可以用来表示物体的个数,也可以用来表示事物的顺序。
自然数都是整数。
2.说一说,下面的数中,哪些表示顺序?哪些表示个数?
(1)强强家的门牌是132号,聪聪家所在的小区有132户人家。
(2)60个同学排成4列,迪迪排在第3列第12个。
用来表示门牌的次序。
表示小区人家的户数多少。
表示学生的人数。
表示学生队列的个数。
表示迪迪所在列的序号。
表示迪迪位置的序号。
门牌号132号的132表示顺序。
132户人家的132表示个数。
60个同学和4列中的60和4表示个数。
第3列和第12个中的3和12表示顺序。
1、(1)把自然数从小到大排列,999前面的一个数是(
),999后面的一个数是(
)。
(2)796后面的连续五个自然数是
(
)。
998
1000
797、798、799、800、801
练习
2
.把自然数1至200按下面的方法组成A,B,C三组。
想一想:这些数的排列方法是怎样的?A组的数有什么特点?B组、C组的数呢?
大家讨论:
(1)每一组有多少个数?最后一个数各是什么?
(2)B组第7个数是多少?C组第56个数呢?
(3)173是哪一组的第几个数?
A组:1
6
7
12
13
18
……
B组:2
5
8
11
14
17
……
C组:3
4
9
10
15
16
……
2.认识负数
1、看温度计说说你对“零上5℃”和“零下5℃”的理解。
零上5℃
0℃
零上5℃和0℃相比,哪个温度更高?
零上5℃比0℃高5℃。
知识回顾
1、看温度计说说你对“零上5℃”和“零下5℃”的理解。
0℃
零下5℃
0℃和零下5℃相比,哪个温度更高?
零下5℃比0℃低5℃。
零上5℃比0℃高5℃。
零下5℃比0℃低5℃。
“零上温度”和“零下温度”是具有相反意义的量。
看温度是在零上还是在零下,要以什么作标准?
以0℃做标准,比0℃高的是零上温度,比0℃低的是零下温度。
2、迪迪从校门口向东走了3米,强强从校门口向西走了3米,看看他们在什么位置。
迪迪
●
强强
●
“向东路程”和“向西路程”是具有相反意义的量。
它们有什么相同点?
两种具有相反意义的量。
为了表示具有相反意义的量,我们把一种意义的量规定为正,用如:3、5等数来表示,这样的数是正数。正数前面也可以写上“+”(正号)。
把另一种意义相反的量规定为负,在数的前面写上“-”(负号)来表示。如-3、-5等,这样的数是负数。
读作:负三
读作:正三
0既不是正数也不是负数。
3、生活中还有哪些量可以用正数与负数表示?
1.在知识竞赛中,如果把加10分记为+10分,那么扣20分记为(
)。
2.汽车在一条南北走向的公路上行驶,如果规定向北行驶的路程为正,那么汽车向北行驶60千米,记为(
)千米,汽车向南行驶80千米,记为(
)千米。
-20
+60
-80
练习
3.某仓库把运进大米吨数记为正,则-4吨表示(
),+6吨表示(
)。
4.如果+5表示转盘向逆时针方向转5圈,那么-3表示(
)。
运出4吨
运进6吨
顺时针方向转3圈
3.整除
商是整数而没有余数,我们可以说:
6能被3整除,也能被2整除。
……
知识回顾
商是整数而有余数,我们可以说:
6不能被4整除。
……
整数a除以整数b(b≠0),所得的商是整数,余数是0,就说a能被b整除。
1、被除数和除数都是整数。
2、商是整数。
3、商后没有余数。
第一个数能被第二个数整除需要满足什么条件?
1、240÷60=6,(
)能被(
)整除。
240
60
2、在36,9,4,12这几个数中,选择两个说一说它们的整除关系。
36能被9整除。
36能被4整除。
12能被4整除。
36能被12整除。
练习
3、15能被哪些数整除?你能用15个小正方形拼成的长方体来表示吗?
15能被1、3、5、15整除。
4、看图说一说什么数能被什么数整除,什么数不能被什么数整除。
18不能被4整除。
18不能被5整除。
14不能被3整除。
5、看图说一说什么数能被什么数整除,什么数不能被什么数整除。
7能被7整除。
7能被1整除。
18能被6整除。
18能被3整除。
4.能被2、5整除的数
1、在1~50的自然数中,分别找出能被4和6整除的数。
被4整除
被6整除
4
8
12
16
20
24
28
32
36
40
44
48
6
12
18
24
36
42
48
知识回顾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
在1~100的自然数中,找出能被5整除的数,用红笔圈出来;找出能被2整除的数,用紫笔圈出来。
能被2整除的数有什么特征?
能被2整除的数的特征:个位上是0、2、4、6、8。
一个正整数,如果能被2整除,这个数叫做偶数;如果不能被2整除,这个数叫做奇(jī)数。
最小的奇数是1,最小的偶数是0。
你知道吗?
能被5整除的数有什么特征?
能被5整除的数的特征:个位上是0或5。
1、能被2整除的数的特征:
2、能被5整除的数的特征:
整数
正整数
零
负整数
自然数
奇数
偶数
最小的奇数是1,最小的偶数是0。
个位上是0、2、4、6、8的数
个位上是0或5的数
1.下面哪些数能被2整除?为什么?
18
27
30
85
423
76
314
个位上是0、2、4、6、8的数能被2整除。
练习
2.下面哪些数能被5整除?为什么?
30
76
85
370
553
1310
504
个位上是0或5的数能被5整除。
3.把下列各数分别按要求填在相应的圈内。
76
83
293
438
199
2054
977
奇数
偶数
83、293、199、
977、
76、438、2054
4.同时能被2和5整除的数有什么特征?举例说明。
个位上是0、2、4、6、8的数能被2整除。
个位上是0或5的数能被5整除。
个位上是0数能被2和5整除。
10、20、30、40、50、60、70、……
5.用0,1,5这三个数字组成的三位数。
(1)能被2整除的数有(
)。
(2)能被5整除的数有(
)。
(3)既能被2整除,又能被5整除的数有
(
)。
150、510
105、150、510
150、510
5.能被3整除的数
在下面的数中分别找出能被2和5整除的数。
被2整除的数
被5整除的数
18
24
30
36
40
42
46
50
80
100
25
30
40
45
50
65
80
100
35
18
24
25
30
35
36
40
42
45
46
50
65
80
100
能被3整除的数有什么特征?
知识回顾
1、根据数位表中的小棒数,完成下表。
摆出的数
用小棒的根数
是否能被3整除
12
3
√
21
3
√
22
4
×
24
36
观察上面的结果,你发现了小棒的根数与能否被3整除有什么关系?
6
9
7
12
57
43
×
√
√
√
2、从10~50自然数中找出能被3整除的数,分别把个位、十位上的数相加,并把和填在下表中。
18
9
21
3
24
6
27
9
30
3
33
6
36
9
39
12
42
6
45
9
48
12
观察个位、十位上的数相加的和,你发现了什么?
一个数各个数位上的数字的和能被3整除,这个数就能被3整除。
1.你报我答。判断报出的数能否被3整除。
48。
是。
73
……
练习
2.在
里填上一个数字,使这个数能被3整除,各有几种填法?
4
2
1
5
2
5
8
1
4
7
0
3
6
9
6.倍数与因数
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
运动会上两个班同学分别排出下面两种队形,算一算两班各有多少人。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9×4=36(人)
5×7=35(人)
知识回顾
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9×4=36(人)
4×9=36(人)
36是9和4的倍数,
9和4是36的因数。
5×7=35(人)
7×5=35(人)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35是5和7的倍数,
5和7是35的因数。
根据算式说一说哪个数是哪个数的倍数,哪个数是哪个数的因数。
25×3=75
20×5=100
在25×3=75中,75是25和3的倍数,25和3是75的因数。
在20×5=100中,100是20和5的倍数,20和5是100的因数。
如果a×b=c(a,b,c是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。
判断:3是因数,18是倍数。(
)
×
3×6=18,我们可以说3是18的因数,18是3的倍数。单独的3和18不能说是因数或倍数。
下面哪些数是7的倍数?与同伴交流你的想法。
7
14
17
25
77
7=7×1
14=7×2
77=7×11
所以7,14,77是7的倍数。
下面哪些数是7的倍数?与同伴交流你的想法。
7÷7=1
14÷7=2
17÷7=2……3
所以7,14,77是7的倍数。
25÷7=3……4
77÷7=11
7
14
17
25
77
7的倍数
1×7=7
7,14,21,28,35,42,49,…都是7的倍数。
2×7=14
3×7=21
4×7=28
5×7=35
6×7=42
7×7=49
8×7=56
9×7=63
……
一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
你能找出24的因数吗?
根据乘法算式找出24的因数。
1×24=24
2×12=24
3×8=24
4×6=24
1和24是24的因数
2和12是24的因数
3和8是24的因数
4和6是24的因数
如何根据除法算式找出24的因数?
1×24=24
2×12=24
3×8=24
4×6=24
24÷1=24
24÷2=12
24÷3=8
24÷4=6
24的因数有:
1、2、3、4、6、8、12、24。
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
你能找出24的因数吗?
1.分别找出18和20的所有因数。
18
3
6
2
9
1、2、3、6、9、18。
20
2
10
4
5
1、2、4、
5、10、20。
练习
2.分别找出4和5的倍数。
8
12
16
20
4、8、12、
16、20……
10
15
20
25
5、10、15、
20、25……
7.素数与合数
1.用若干个小正方形拼成长方形的方法,研究3,4,5,6这几个数分别有哪些因数。
3的因数:1,3。
4的因数:1,2,4。
知识回顾
1.用若干个小正方形拼成长方形的方法,研究3,4,5,6这几个数分别有哪些因数。
5的因数:1,
5
6的因数:1,2,3,6
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
1的因数有
2的因数有
3的因数有
4的因数有
5的因数有
6的因数有
1
1,2
1,3
1,2,4
1,5
1,2,3,6
7的因数有
8的因数有
9的因数有
10的因数有
11的因数有
12的因数有
1,7
1,2,4,8
1,3,9
1,2,5,10
1,11
1,2,3,4,6,12
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
只有一个因数
只有1和它本身两个因数
至少有三个因数
1
2,3,5,7,11
4,6,8,9,10,12,
填写1至20各数的全部因数,再根据因数的个数,把自然数分类。
一个数如果除了1和它本身,还有别的因数,这样的数叫做合数。
1的因数只有1,1既不是素数,也不是合数。
只有一个因数
只有1和它本身两个因数
至少有三个因数
1
2,3,5,7,11
4,6,8,9,10,12,
一个数,如果只有1和它本身两个因数,这样的数叫做素数(也叫质数)。
1
2,3,5,7,11
4,6,8,9,10,12,
判断下列各数中哪些是素数,哪些是合数。
17
22
29
35
37
87
93
96
素数:17,29,37。
合数:22,35,87,93,96。
找出下表中的素数。
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
把100以内的素数在下表中涂色表示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
把100以内的素数在下表中涂色表示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
(1)观察100以内的数表,素数是怎样分布的?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
除2、3以外,素数大都分布在6的倍数的两边,但6的倍数两边的数不一定都是素数。
(2)在以4或6为首的一列数中,有没有素数?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
没有。以4为首和以6为首的两列数分别是2和3的倍数。
(3)选几个素数,分别除以6,它们的余数有什么特点?
7÷6=1……1
100以内的素数。
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
11÷6=1……5
13÷6=2……1
17÷6=2……5
19÷6=3……1
23÷6=3……5
29÷6=4……5
31÷6=5……1
余数为1或者5。
自然数
因数
自然数
因数
15
32
19
37
21
41
28
45
1.写出下面各数的因数。
1,3,5,15
1,19
1,3,7,21
1,2,4,7,14,28
1,2,4,8,16,32
1,37
1,41
1,3,5,9,15,45
练习
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2.探索。
(1)先划去1,再一次划去2,3,5,7的倍数
(2,3,5,7除外)。
(2)没有划去的数都是素数吗?
是
3.在
里填既是素数,又是奇数的数。
24=
+
8=
+
10=
+
12=
+
22=
+
16=
+
11
13
3
5
3
7
5
7
5
17
5
11
4.把下面的自然数分成两类。
21、29、45、51、73、81、91、97、
(1)素数:(
)。
(2)合数:(
)。
5.按顺序说出20以内的全部素数,看谁说得快。
29、73、97、
21、45、51、81、91
2、3、5、7、11、13、17、19
6.判断。
(1)正整数除了1,不是素数就是合数。(
)
(2)9既是奇数,又是合数。(
)
(3)13的因数都是素数。(
)
7.在两位数的素数中:
(1)个位是1的有(
)
(2)个位是3的有(
)
(3)个位是7的有(
)
(4)个位是9的有(
)
√
√
×
11、31、41、61、71
13、23、43、53、73、83、
17、37、47、67、97
19、29、59、79、89
8.写出5个素数,把它们从小到大排列起来,使相邻两个数的差都是6。
5、11、17、23、29、
8.分解素因数
下面各数中哪些是素数,哪些是合数?分别填入指定的圈里。
素数
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
合数
知识回顾
你能把30写成几个素数相乘的形式吗?
先把30分解成两个数相乘的形式,30分解成5×6。
5是素数,不需要再分解;6是合数,需要再进行分解,6分解成2×3。
30
5
6
2
3
你能把30写成几个素数相乘的形式吗?
还可以把30先分解成2×15或3×10,然后再进行分解。
30
2
15
3
5
30
3
10
2
5
无论怎样分解,30都能分解为2、3、5这3个素数相乘的形式。
你能把30写成几个素数相乘的形式吗?
还可以用短除法进行分解。
把要分解的数30写在短除号里。
用30的因数中的素数去除,一般从最小的素数开始。
30
2
用2去除,2是素数。
直到商是素数为止。
15
5
3
15是3的倍数,用3去除,3是素数。
5是素数,分解结束。
把除数和商写成相乘的形式。
30=2×3×5
你能把30写成几个素数相乘的形式吗?
也可以按如下方式分解:
30
5
6
2
3
30
3
10
2
5
30=2×3×5
30=2×3×5
30
5
6
2
3
30
15
5
3
2
30=2×3×5
30可以写成素数2、3、5相乘的形式,2、3、5叫做30的素因数。
把一个合数写成用素因数相乘的形式表示出来,叫做分解素因数。
你能把30写成几个素数相乘的形式吗?
1、把下面各数分解素因数。
24
35
45
77
84
24=2×2×2×3
35=5×7
45=3×3×5
77=7×11
84=2×2×3×7
练习
2、把36、48、60这三个数分解素因数,并指出这三个数有哪些公有的素因数。
36=2×2×3×3
48=2×2×2×2×3
60=2×2×3×5
公有的是2,2,3
3、写出三组成倍数关系的数,并将它们分解素因数。你发现了什么?
6=2×3
36=2×2×3×3
216=2×2×2×3×3×3
……
整理与应用
一
1、填空。
(1)在1,2,3,6,9,17,24,71,80这些自然数中:
(
)是素数,(
)是合数;
(
)是奇数,(
)是偶数;
(
)既是偶数又是素数,(
)既是奇数又是合数。
(2)因为45能被(
)整除,所以45的因数有(
)。
2,3,17,71
6,9,24,80
1,3,9,17,71
2,6,24,80
2
9
1,3,5,9,15,45
1,3,5,9,15,45
2、填空。
(3)在54、37、20、75、87、95这些数中,2的倍数有(
),3的倍数有(
)5的倍数有(
)。
(4)在算式3×5×7=105中,3,5,7是105的(
)。
(5)规定盈利为正,某公司去年亏损18000元,记为(
)元,今年盈利25000元,记为
(
)元。
素因数
-18000
+25000
54,20,
54,75,87
20,75,95
3、先读一读下面的数,再把它们填入对应的圈内。
-6
+15
0
20
-30
-100
50
正数
负数
+15,20,50
-6,-30,-100
4、先把560分解素因数,再写出两个因数相乘积都是560的式子。
(
)×(
)=(
)×(
)
560=2×2×2×2×5×7
7
80
35
16
5、在横线上填上合适的数。
90×8=
×(8+2)
25×(10+
)=35×10
36×20=24×(
+10)
35×(14+2)=
×14
72
4
20
40
类别
童话
少儿科技
智力游戏
故事
数量/本
57
71
93
105
6、下面各种图书分别能平均分给3个班吗?
童话书、智力游戏书、故事书能平均分给3个班。
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
中间各停靠站上车33人,下车49人,共82人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(1)中间各停靠站上、下车共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
从A站驶向B站时,车上共有36人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(2)从A站驶向B站时,车上共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
从D站驶向E站时,车上共有31人。
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(3)从D站驶向E站时,车上共有多少人?
7、
下表记录了一辆308路公共汽车全程载客数量的情况。(正数为上车人数,负数为下车人数)
公交车到达体育馆时,车上还剩多少人?
站名
南山路
中间停靠站
体育馆
A
B
C
D
E
F
G
上、下车人数
+32
+8
+7
+5
+6
+4
+3
0
-16
-4
-5
-10
-8
-9
-5
-8
(4)你还能提出哪些数学问题?
谢
谢
同课章节目录
- 一 自然数与整数
- 1.自然数
- 2.认识负数
- 3.整除
- 4.能被2,5整除的数
- 5.能被3整除的数
- 6.倍数与因数
- 7.素数与合数
- 8.分解因数
- 二 可能性
- 9.认识可能性
- 三 分数与除法
- 10.分数与除法的关系
- 11.一个数是另一个数的几分之几
- 12.真分数与假分数
- 13.假分数与整数
- 14.假分数与带分数
- 四 几何小天地
- 15.角的度量
- 16.角的分类
- 17.轴对称图形
- 18.图形的旋转
- 19.三角形的边
- 20.三角形的角
- 21.三角形内角和
- 22.平行四边形的边与角
- 23.梯形的边与角
- 24.图形的高与底
- 五 代数式与方程
- 25.代数式(一)
- 26.代数式(二)
- 27.认识方程
- 28.等式的性质
- 29.解方程
- 30.列方程解题(一)
- 31.列方程解题(二)
- 六 总复习
