四年级下册数学课件-四 几何小天地 复习课件 浙教版 (共115张PPT) (1)
文档属性
| 名称 | 四年级下册数学课件-四 几何小天地 复习课件 浙教版 (共115张PPT) (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 00:00:00 | ||
图片预览




文档简介
(共115张PPT)
四
几何小天地
复习课件
知识的梳理
线段、射线和直线(数线段)
位置关系(点到直线的距离、垂直与平行)
图形的变换——认识圆、认识角
几何小天地
15.角的度量
从一点可以引出无数条射线。
射线:只有一个端点,可以向一端无限延伸。不可度量长度。
复习
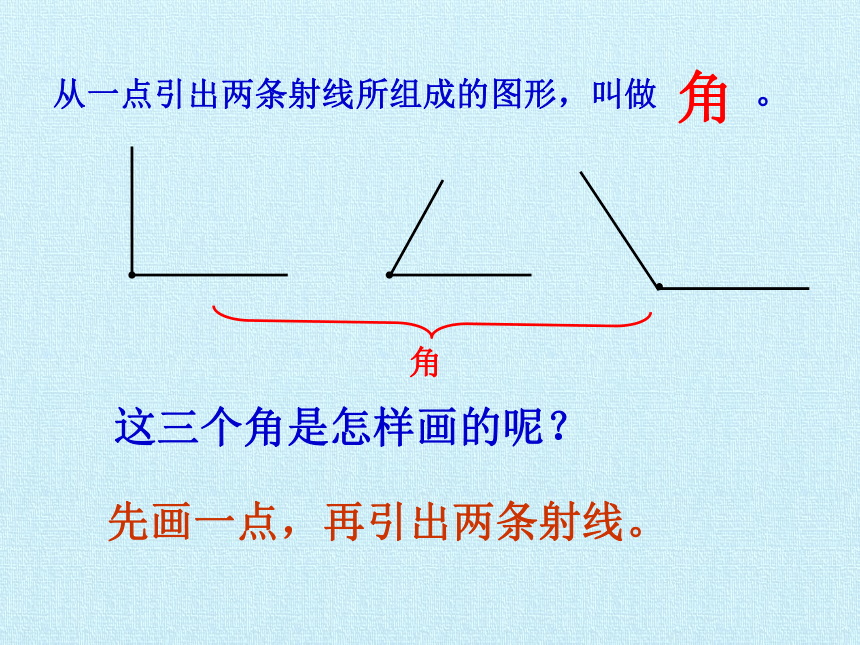
这三个角是怎样画的呢?
先画一点,再引出两条射线。
角
从一点引出两条射线所组成的图形,叫做
。
角
量
角
器
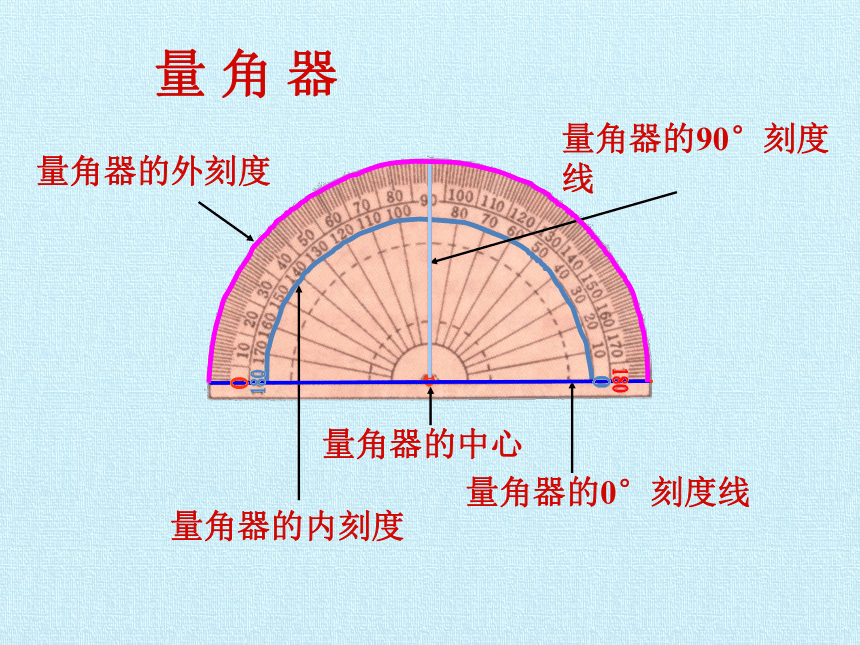
量角器的中心
量角器的0°刻度线
量角器的内刻度
量角器的外刻度
量角器的90°刻度线
0
0
0
0
0
0
0
0
0
0
180
180
180
180
180
180
180
180
180
180
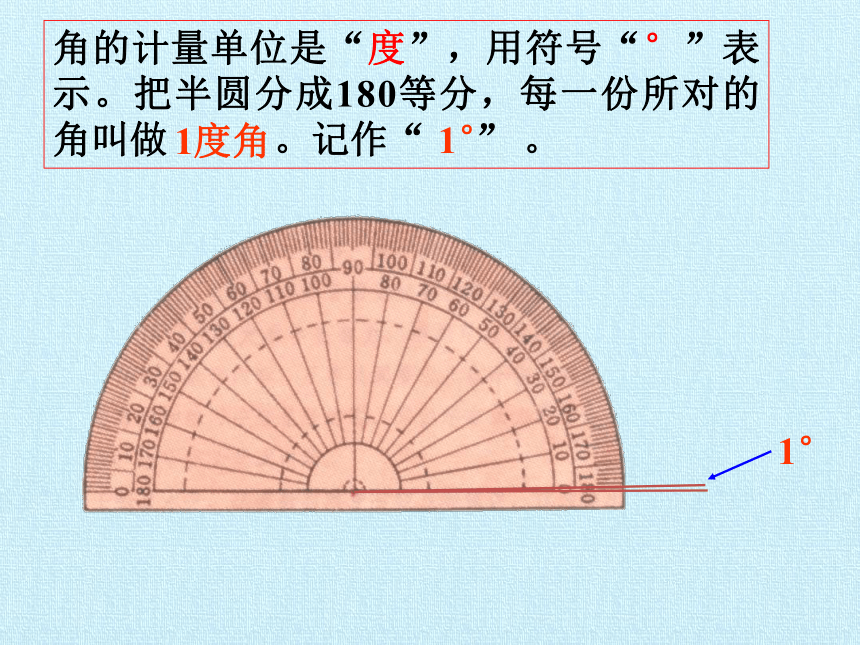
角的计量单位是“度”,用符号“°”表示。把半圆分成180等分,每一份所对的角叫做
。记作“
”
。
1度角
1°
1°
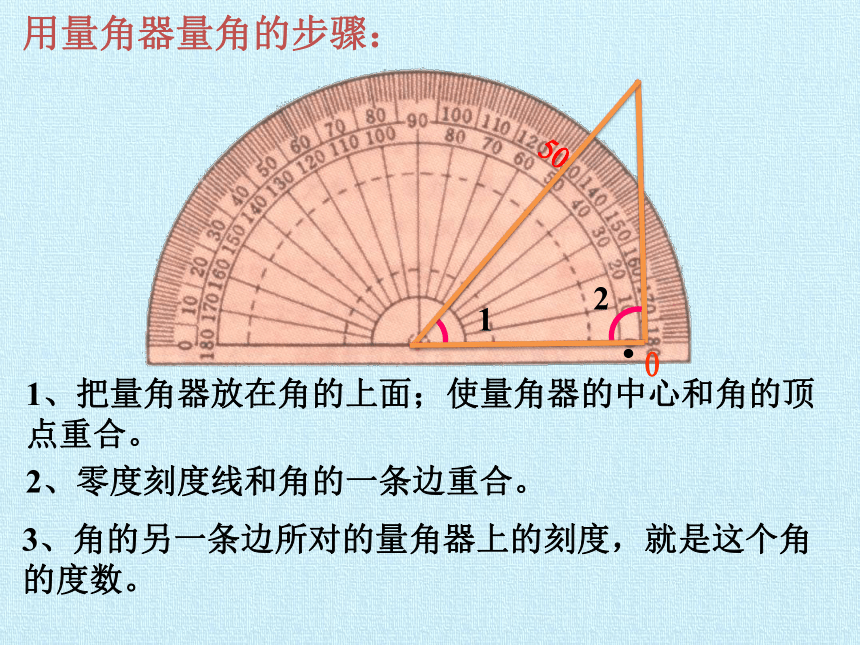
用量角器量角的步骤:
1、把量角器放在角的上面;使量角器的中心和角的顶点重合。
2、零度刻度线和角的一条边重合。
3、角的另一条边所对的量角器上的刻度,就是这个角的度数。
50
0
1
2
·
(1)画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合。
(2)在量角器65°刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,再画一条射线。
60
(4)画完后在角上标上符号,写出度数。
画60°角的步骤:
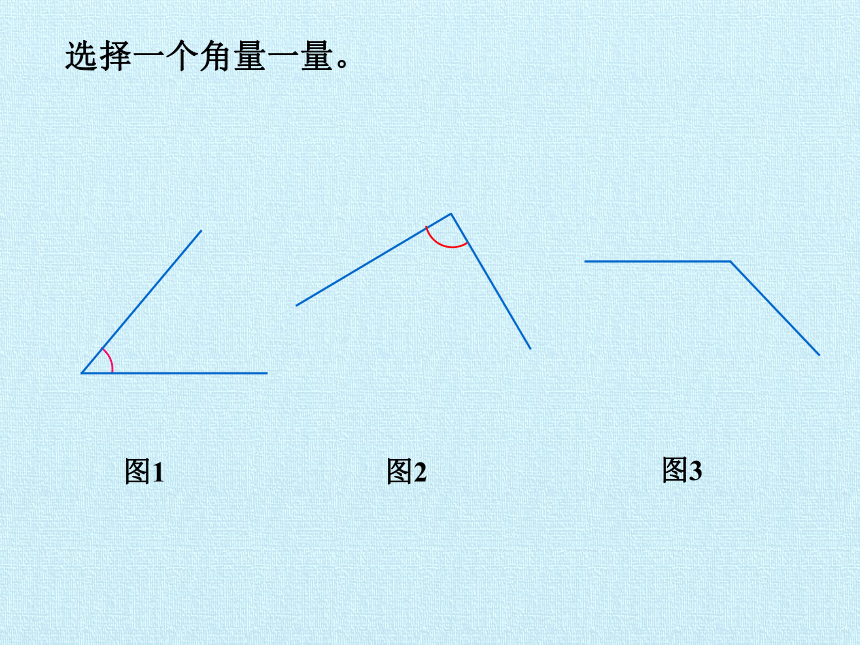
选择一个角量一量。
图1
图2
图3
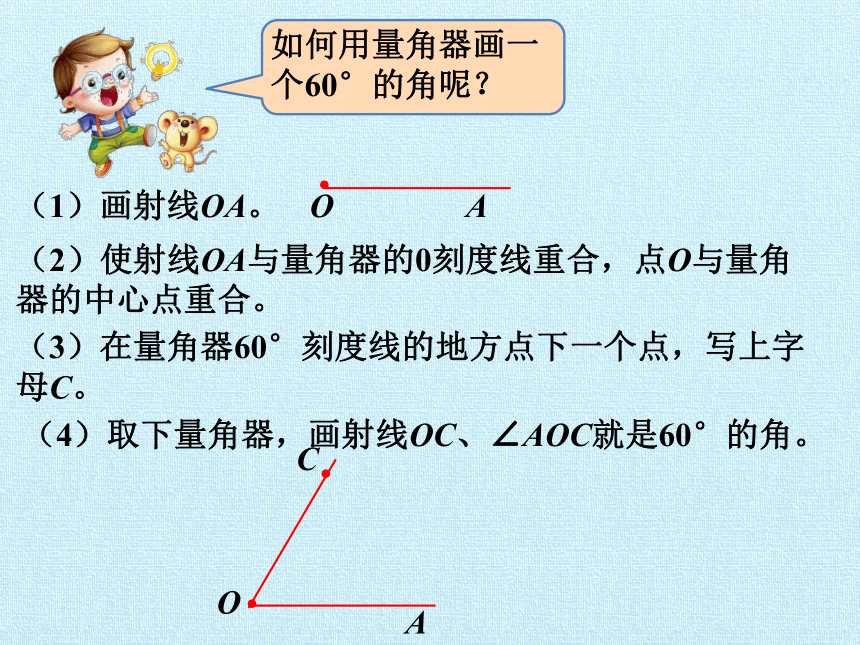
如何用量角器画一个60°的角呢?
(1)画射线OA。
(2)使射线OA与量角器的0刻度线重合,点O与量角器的中心点重合。
(3)在量角器60°刻度线的地方点下一个点,写上字母C。
(4)取下量角器,画射线OC、∠AOC就是60°的角。
C
O
A
O
A
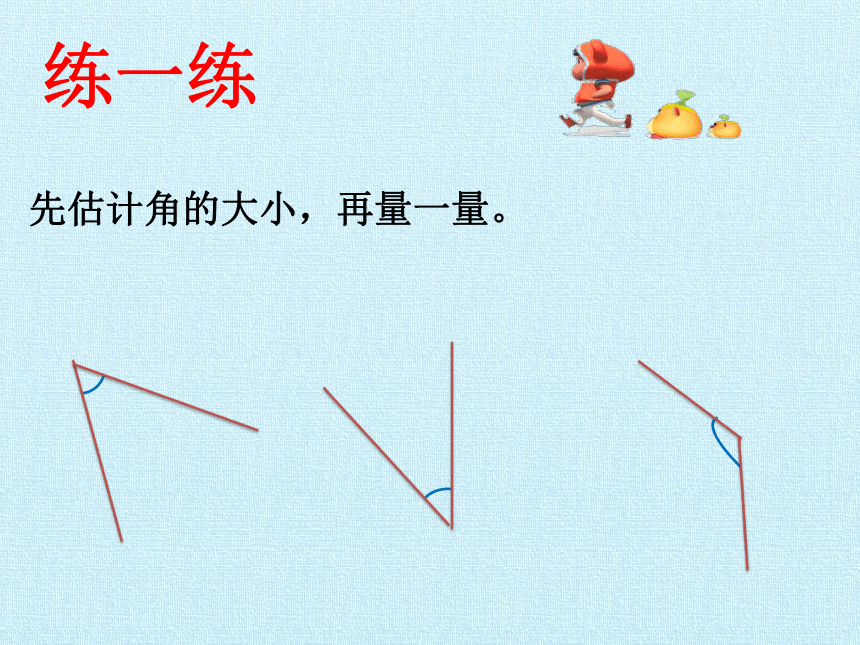
先估计角的大小,再量一量。
练一练
度量一个角,角的一条边对着量角器上内圈“0”的刻度,另一条边对着内圈刻度“60”,这个角是(
)。
A.60°
B.180°
C.20°
A
拓展训练
量出下面各图中角的度数。
三个角的度数和是(
)
三个角的度数和是(
)
180°
180°
16.角的分类
因为它们的度数都是90°,都是直角。
一个直角是90度
注意:直角是一种特殊角,它的度数是固定不变的,是90°。
这种角叫做平角。
因为它比较特殊,角的两边成一条直线,它的度数刚好是180度。
注意:1平角=2直角
因为这三个角的度数都小于90度。
大于0°而小于90°的角,叫做锐角。
补充条件:因为它们的度数既大于90°,又小于180°。
这叫做钝角
这是周角。
注意:1周角=2平角=4直角
.
O
A
角的一边绕顶点旋转一周,与另一边重合,这时所形成的角叫做周角。周角是360°。
因为它们的度数都是90度,都是直角。
一个直角是90度的角叫做直角
注意:直角是一种特殊角,它的度数是固定不变的,是90度。
两个直角拼在一起形成的角是180°,这个角叫做平角。
平角的两边成一条直线
注意:1平角=2直角
.
大于0°而小于90°的角叫做锐角。
锐角
钝角
大于90°而小于180°的角叫做钝角。
.
O
A
角的一边绕顶点旋转一周,与另一边重合,这时所形成的角叫做周角。周角是360°。
注意:1周角=2平角=4直角
两块三角板公有6个角。用两块三角板拼角,你能拼出几种不同的角?
①
.
思考:1、刚才我们把角分成了哪几类?
2、按从大到小的顺序应怎样排列?
3、它们分别有什么特征?
名称:
周角
平角
钝角
直角
锐角
特征:等于
360度
等于
180度
等于
90度
大于90度
小于180度
大于0度
小于90度
O
E
A
D
C
B
∠BOC是(
)角。
∠BOD是(
)角。
∠AOD是(
)角。
∠AOE是(
)角。
巩固练习
1、80°的角与(
)°的角能拼成一个直角。
2、一个直角与一个锐角的和,一定是(
)角。
3、一个平角与一个锐角的差,一定是(
)角。
判断
10
钝
钝
1、直角总是90°。
(
)
2、锐角都小于90°。
(
)
3、大于90?的角叫钝角。
(
)
4、钝角都大于90°。
(
)
口答
√
√
×
√
17.轴对称图形
下面第一行的四个图形顺着虚线对折后,会变成第二行四个图形中的那一个?用线连一连。
一个图形对折后能够完全重合,这个图形就是轴对称图形。折痕所在的直线就是这个轴对称图形的对称轴。
先找出轴对称图形,在画出轴对称图形的对称轴。
A
有些图形有多条对称轴。在画一个轴对称图形的对称轴时,要考虑多个方向。
下列图案哪些是轴对称图形?是的指出它们的对称轴。
画一画五角星有几条对称轴?
在方格纸上,根据给出的对称轴,画出轴对称图形,并说一说你是怎么画的。
知识拓展
想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车车牌的号码吗?
答:MT7936
如图是在平面镜中看的钟表,你能告诉老师现在几点了么?
答:2:35
18.图形的旋转
.
.
A
B
想一想,画一画
线段AB绕着点A向逆时针方向旋转45度,先画出线段AB的位置,在画出点B经过的路线。如果是旋转90度呢?
.
.
A
B
N
M
以点A为顶点,AB为角的一边,在用量角器量出45度的角,AM就是AB旋转后的位置。再以点A为圆心,以AB长为半径画圆,曲线BM就是B经过的路线。
.
.
线段AN就是AB向逆时针方向旋转后的位置。曲线BN就是点B经过的路线。
动手画出线段AK绕着点A向逆时针方向旋转90度后的位置,并画出K点经过的路线。如果是135度呢?
.
.
A
B
N
M
.
.
K
.
.
.
P
Q
AK旋转90度后的位置为AP,路线为KP。
AK旋转135度后的位置为AQ,路线为KQ。
随堂练习
12
1
2
3
4
5
6
7
8
9
10
11
O
指针从“12”到“1”,指针绕点O
顺时针旋转了30°
。
指针从“1”到(
),指针绕点O
顺时针旋转了60°
。
指针从“3”到“6”,指针绕点O
顺时针旋转(
)
。
3
90
°
想一想,画一画
长方形ABCD绕着点A向顺时针方向旋转90度后的位置。
A
B
D
C
.
.
.
.
A
B
D
C
.
.
.
F
E
G
.
.
.
.
(1)线段AB绕点A向顺时针方向旋转90度后,点B应该在那个位置?
(2)线段AC绕点A向顺时针方向旋转90度后,点C应该在那个位置?
(3)线段AD绕点A向顺时针方向旋转90度后,点D应该在那个位置?
长方形AGEF就是绕点ABCD向顺时针。
A
B
D
C
E
G
.
.
.
请画出长方形ABCD绕点D向顺时针方向旋转90度后的位置。
.
.
.
F
.
A
O
D
E
45°
点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;旋转的角度是___。
问题一
B
E
OE
DE
45°
练习
C
B
A
D
F
E
O
如图,将△ABC绕着外面的点O旋转60°将整个△ABC旋转到△DEF的位置。
点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;旋转的角度是___。
问题二
F
FE
DF
60°
19.三角形的边
长度/cm
3
4
5
7
8
数量/根
2
3
1
1
1
从下面的小棒中选3根,摆出不同的三角形。
围成三角形的三条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
三角形的三个顶点通常用三个字母表示,三角形用符号“△”表示,右面的三角形可以记做“△ABC”,读作“三角形ABC”。三角形的三个边可以读作AB边、BC边、AC边。
A
B
C
和同学一起讨论,把下面的三角形按边分一分。把编号填在相应的柜里。
任意两边都不相等
两边相等
三边都相等
⑤、⑥、⑧
①、③、④、⑨
②、⑦
①
②
③
④
⑤
⑥
⑦
⑧
⑨
两条边相等的三角形叫做等腰三角形。
三边相等的三角形叫做等边三角形,又叫做正三角形。
等腰三角形里,相等的两条边叫做腰,另一条边叫做底。两腰的夹角叫做顶角,腰和底的夹角叫做底角,两个底角相等。
顶角
底角
底角
腰
腰
点
等腰三角形是特殊的三角形,等边三角形又是特殊的等腰三角形。
用三根木条钉成一个三角形,用力拉,这个三角形不会变形。这就是三角形的稳定性。
生活中哪些地方利用了三角形的稳定性?
有长度不相等的一些小棒:
①
②
③
④
⑤
3cm
7cm
5cm
4cm
9cm
选三根搭一个三角形。
选择①,②,④可以搭一个三角形。
你还能选3跟搭一个三角形吗?选②,④,⑤能搭一个三角形吗?为什么?
A
B
C
想一想,在三角形ABC中,下面的关系式是否成立?为什么?
AB+AC>BC
BA+BC>AC
CA+CB>AB
三角形任意两边的和大于第三边。
随堂练习
1.用同样长度的小棒搭成如右图所示的形状,一共用了几根小棒?有多少个三角形?
9根小棒
5个三角形
2.用同样长度的小棒(火柴棒或牙签)3根、4根、5根、6根、7根、8根……搭三角形,把搭的结果填在表格里。
小棒根数
3
4
5
6
7
8
能否搭成三角形
能
不能
能
不能
能
不能
搭成三角形的个数
1
2
3
三角形的类型
等边
等边
等边
下列长度的各组线段,能构成三角形的是:
A.
5cm、4cm、3cm
B.
9cm、5cm、4cm
C.
7cm、4cm、2cm
答:A
知识巩固
从A点到B点,最短的路径是哪一条?若要与过C点的路径比较,谁的路程远呢?
A
B
C
根据线段的基本性质有:AB<AC+BC
20.三角形的角
三个角都是锐角的三角形叫做锐角三角形。
有一个角是钝角的三角形叫做钝角三角形。
别忘了还有直角三角形。
有一个角是直角的三角形叫做直角三角形。
三角形按角分
锐角三角形
钝角三角形
直角三角形
(3个角都是锐角的三角形)
(有1个角是直角的三角形)
(有1个角是钝角的三角形)
A
B
C
}
}
直角三角形
锐角三角形
钝角三角形
开动你的大脑思考下
△ABC的顶点A在直线上运动,可以形成哪些三角形?
21.三角形内角和
所有三角形的内角和都是180度吗?
?
所有三角形的内角和都是180度!
那我们来看看怎样来解题呢。
解法一:
解法二:
1、在△ABC中,∠C=78°,∠B=44°,求∠A。
∠A=180°-78°-44°
=102°-44°
=58°
∠A=180°-(78°+44°)
=180°-122°
=58°
2、等腰直角三角形的两个底角各是多少度?
∠B=∠A
=(180°-90°)÷2
=45°
A
B
C
一个直角三角形中最多有( )个直角,
为什么?
一个钝角三角形中最多有( )个钝角,
为什么?
练一练
1
1
1、填空
2、一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
180°-70°×2
180°-70°
-70°
70°
70°
40°
内角和180°
180°-90°-50°=40°
180°-(50°+90°)=40°
3、一个直角三角形,一个锐角是50°,另一个锐角是几度?
50°
90°-50°=40°
?
A、比90°小
B、比90°大
C、可能等于90°,大于90°或小于90°
D、还是180°
①把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和(
)
D
拓展训练
A.一定是锐角
B.一定是钝角
C.一定是直角
D.可能是锐角或钝角或直角。
②一个三角形,有两个角是锐角,则第三个角(
)
D
判断
(1)三角形的内角和是180°。(
)
(2)钝角三角形的内角和比锐角三角形的大。(
)
(3)三角形越大,它的内角和就越大。(
)
√
×
×
22.平行四边形的边与角
像这样两组对边分别平行的四边形叫做平行四边形。
(1)
(2)
(3)
(4)
(5)
(6)
长方形和正方形的两组对边都互相平行。
那么我们再看看下列图形中哪些是平行四边形?
所以:长方形和正方形它们都是特殊的平行四边形。
我还可以用图形表示长方形、正方形和平行四边形的关系。
平行四边形
长方形
正方形
你可以想到什么?
两组对边分别相等。
例、像右图那样,从长方形中剪下一个直角三角形,把它平移到另一侧,可以拼成一个平行四边形。
例、剪一些平行四边形
把它们的对角线分别重叠起来,重叠∠A,∠C。重叠∠B,∠D。
你会有什么发现?
两组对角分别相等。
练一练
特征
平行四边形
长方形
正方形
对边平行
对边相等
四边相等
对角相等
四个角都是直角
1、根据平行四边形、长方形、正方形的特征在
里画√。
√
√
√
√
√
√
√
√
√
√
√
√
2、把点与点连接起来,画出两个面积不等的平行四边形。
3、下面每组两个图形的大小有什么关系?剪一剪,拼一拼,想一想。
1、下面图形中是平行四边形的打上“√”。
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
√
√
√
√
2
3
4
5
6
7
8
拓展练习
1
2、填空题:
平行四边形的对边(
)而且(
),对角(
)。
平行
相等
相等
23.梯形的边与角
构成的图形是哪一类四边形?
只有一组对边平行的四边形叫做梯形。
我们把只有一组对边平行的四边形叫做梯形。
上底
下底
腰
腰
互相平行的一组对边分别叫做梯形的上底和下底,
不平行的一组对边叫做梯形的腰。
判断下面图形哪些是梯形,是的和不是都说出理由。
是
是
1.生活中你在哪些地方见过梯形呢?
梯子
沟渠横截面
堤坝横截面
2.思考一下
把长方形像右图那样剪开,就得到了两个梯形。
想一想,这是为什么?
腰相等
腰相等
3.用彩色笔画出下面梯形的腰,两腰相等吗?你是怎样发现的?
两腰相等的梯形叫做等腰梯形。
(1)观察下面梯形,它们的角有什么特别的地方?
梯形②和④中有直角。
像这样有直角的梯形叫做直角梯形。
4.
(2)观察下面梯形,它们的角有什么特别的地方?
上图中哪些是等腰梯形?
①和③
上底
下底
腰
腰
其中哪些角相等?
1
2
3
4
∠1=∠2
∠3=∠4
把点与点连接起来,画出两个形状不同的梯形。
练一练
找出下图中的梯形,并指出梯形的上底、下底和高。
平行四边形
梯形
梯形
梯形
下底
上底
上底
下底
上底
下底
拓展练习
24.图形的高与底
1、从三角形的一个顶点向它的对边作一条垂线,顶点和垂足间的线段叫做三角形的高,
三角形的高
这条对边叫做三角形的底。
底
三角形的高
底
2、从平行四边形一条边上的一点向对边作一条垂线,
平行四边形的高
这个点和垂足间的线段叫做平行
四边形的高,
这条对边叫做平行四边形的底。
底
高
底
3、从梯形上底的一点向下底作一条垂线,
这个点和垂足间的线段叫做梯形的高。
高
高
高
底
4、画三角形的高:先把三角尺的一条直角边与三角形的某一条边重合,另一条直角边平移到三角形的顶点,从这个顶点沿着三角尺的直角边向该线画垂线,这条垂线就是三角形这条边上的高。
练一练:
1、根据三角形的底,用三角尺画出他们的高。
底
高
底
高
底
高
2、根据平行四边形的底,用三角尺画出他们的高。
底
高
底
高
底
高
3、描出梯形的高。
下底
上底
上底
下底
下底
上底
1、判断下面的蓝色线段是平行四边形的底和高吗?是的话,哪条是底,哪条是高?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
拓展练习:
2、画出每个三角形底边上的高。
底
底
高
高
高
底
谢
谢
四
几何小天地
复习课件
知识的梳理
线段、射线和直线(数线段)
位置关系(点到直线的距离、垂直与平行)
图形的变换——认识圆、认识角
几何小天地
15.角的度量
从一点可以引出无数条射线。
射线:只有一个端点,可以向一端无限延伸。不可度量长度。
复习
这三个角是怎样画的呢?
先画一点,再引出两条射线。
角
从一点引出两条射线所组成的图形,叫做
。
角
量
角
器
量角器的中心
量角器的0°刻度线
量角器的内刻度
量角器的外刻度
量角器的90°刻度线
0
0
0
0
0
0
0
0
0
0
180
180
180
180
180
180
180
180
180
180
角的计量单位是“度”,用符号“°”表示。把半圆分成180等分,每一份所对的角叫做
。记作“
”
。
1度角
1°
1°
用量角器量角的步骤:
1、把量角器放在角的上面;使量角器的中心和角的顶点重合。
2、零度刻度线和角的一条边重合。
3、角的另一条边所对的量角器上的刻度,就是这个角的度数。
50
0
1
2
·
(1)画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合。
(2)在量角器65°刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,再画一条射线。
60
(4)画完后在角上标上符号,写出度数。
画60°角的步骤:
选择一个角量一量。
图1
图2
图3
如何用量角器画一个60°的角呢?
(1)画射线OA。
(2)使射线OA与量角器的0刻度线重合,点O与量角器的中心点重合。
(3)在量角器60°刻度线的地方点下一个点,写上字母C。
(4)取下量角器,画射线OC、∠AOC就是60°的角。
C
O
A
O
A
先估计角的大小,再量一量。
练一练
度量一个角,角的一条边对着量角器上内圈“0”的刻度,另一条边对着内圈刻度“60”,这个角是(
)。
A.60°
B.180°
C.20°
A
拓展训练
量出下面各图中角的度数。
三个角的度数和是(
)
三个角的度数和是(
)
180°
180°
16.角的分类
因为它们的度数都是90°,都是直角。
一个直角是90度
注意:直角是一种特殊角,它的度数是固定不变的,是90°。
这种角叫做平角。
因为它比较特殊,角的两边成一条直线,它的度数刚好是180度。
注意:1平角=2直角
因为这三个角的度数都小于90度。
大于0°而小于90°的角,叫做锐角。
补充条件:因为它们的度数既大于90°,又小于180°。
这叫做钝角
这是周角。
注意:1周角=2平角=4直角
.
O
A
角的一边绕顶点旋转一周,与另一边重合,这时所形成的角叫做周角。周角是360°。
因为它们的度数都是90度,都是直角。
一个直角是90度的角叫做直角
注意:直角是一种特殊角,它的度数是固定不变的,是90度。
两个直角拼在一起形成的角是180°,这个角叫做平角。
平角的两边成一条直线
注意:1平角=2直角
.
大于0°而小于90°的角叫做锐角。
锐角
钝角
大于90°而小于180°的角叫做钝角。
.
O
A
角的一边绕顶点旋转一周,与另一边重合,这时所形成的角叫做周角。周角是360°。
注意:1周角=2平角=4直角
两块三角板公有6个角。用两块三角板拼角,你能拼出几种不同的角?
①
.
思考:1、刚才我们把角分成了哪几类?
2、按从大到小的顺序应怎样排列?
3、它们分别有什么特征?
名称:
周角
平角
钝角
直角
锐角
特征:等于
360度
等于
180度
等于
90度
大于90度
小于180度
大于0度
小于90度
O
E
A
D
C
B
∠BOC是(
)角。
∠BOD是(
)角。
∠AOD是(
)角。
∠AOE是(
)角。
巩固练习
1、80°的角与(
)°的角能拼成一个直角。
2、一个直角与一个锐角的和,一定是(
)角。
3、一个平角与一个锐角的差,一定是(
)角。
判断
10
钝
钝
1、直角总是90°。
(
)
2、锐角都小于90°。
(
)
3、大于90?的角叫钝角。
(
)
4、钝角都大于90°。
(
)
口答
√
√
×
√
17.轴对称图形
下面第一行的四个图形顺着虚线对折后,会变成第二行四个图形中的那一个?用线连一连。
一个图形对折后能够完全重合,这个图形就是轴对称图形。折痕所在的直线就是这个轴对称图形的对称轴。
先找出轴对称图形,在画出轴对称图形的对称轴。
A
有些图形有多条对称轴。在画一个轴对称图形的对称轴时,要考虑多个方向。
下列图案哪些是轴对称图形?是的指出它们的对称轴。
画一画五角星有几条对称轴?
在方格纸上,根据给出的对称轴,画出轴对称图形,并说一说你是怎么画的。
知识拓展
想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车车牌的号码吗?
答:MT7936
如图是在平面镜中看的钟表,你能告诉老师现在几点了么?
答:2:35
18.图形的旋转
.
.
A
B
想一想,画一画
线段AB绕着点A向逆时针方向旋转45度,先画出线段AB的位置,在画出点B经过的路线。如果是旋转90度呢?
.
.
A
B
N
M
以点A为顶点,AB为角的一边,在用量角器量出45度的角,AM就是AB旋转后的位置。再以点A为圆心,以AB长为半径画圆,曲线BM就是B经过的路线。
.
.
线段AN就是AB向逆时针方向旋转后的位置。曲线BN就是点B经过的路线。
动手画出线段AK绕着点A向逆时针方向旋转90度后的位置,并画出K点经过的路线。如果是135度呢?
.
.
A
B
N
M
.
.
K
.
.
.
P
Q
AK旋转90度后的位置为AP,路线为KP。
AK旋转135度后的位置为AQ,路线为KQ。
随堂练习
12
1
2
3
4
5
6
7
8
9
10
11
O
指针从“12”到“1”,指针绕点O
顺时针旋转了30°
。
指针从“1”到(
),指针绕点O
顺时针旋转了60°
。
指针从“3”到“6”,指针绕点O
顺时针旋转(
)
。
3
90
°
想一想,画一画
长方形ABCD绕着点A向顺时针方向旋转90度后的位置。
A
B
D
C
.
.
.
.
A
B
D
C
.
.
.
F
E
G
.
.
.
.
(1)线段AB绕点A向顺时针方向旋转90度后,点B应该在那个位置?
(2)线段AC绕点A向顺时针方向旋转90度后,点C应该在那个位置?
(3)线段AD绕点A向顺时针方向旋转90度后,点D应该在那个位置?
长方形AGEF就是绕点ABCD向顺时针。
A
B
D
C
E
G
.
.
.
请画出长方形ABCD绕点D向顺时针方向旋转90度后的位置。
.
.
.
F
.
A
O
D
E
45°
点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;旋转的角度是___。
问题一
B
E
OE
DE
45°
练习
C
B
A
D
F
E
O
如图,将△ABC绕着外面的点O旋转60°将整个△ABC旋转到△DEF的位置。
点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;旋转的角度是___。
问题二
F
FE
DF
60°
19.三角形的边
长度/cm
3
4
5
7
8
数量/根
2
3
1
1
1
从下面的小棒中选3根,摆出不同的三角形。
围成三角形的三条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
三角形的三个顶点通常用三个字母表示,三角形用符号“△”表示,右面的三角形可以记做“△ABC”,读作“三角形ABC”。三角形的三个边可以读作AB边、BC边、AC边。
A
B
C
和同学一起讨论,把下面的三角形按边分一分。把编号填在相应的柜里。
任意两边都不相等
两边相等
三边都相等
⑤、⑥、⑧
①、③、④、⑨
②、⑦
①
②
③
④
⑤
⑥
⑦
⑧
⑨
两条边相等的三角形叫做等腰三角形。
三边相等的三角形叫做等边三角形,又叫做正三角形。
等腰三角形里,相等的两条边叫做腰,另一条边叫做底。两腰的夹角叫做顶角,腰和底的夹角叫做底角,两个底角相等。
顶角
底角
底角
腰
腰
点
等腰三角形是特殊的三角形,等边三角形又是特殊的等腰三角形。
用三根木条钉成一个三角形,用力拉,这个三角形不会变形。这就是三角形的稳定性。
生活中哪些地方利用了三角形的稳定性?
有长度不相等的一些小棒:
①
②
③
④
⑤
3cm
7cm
5cm
4cm
9cm
选三根搭一个三角形。
选择①,②,④可以搭一个三角形。
你还能选3跟搭一个三角形吗?选②,④,⑤能搭一个三角形吗?为什么?
A
B
C
想一想,在三角形ABC中,下面的关系式是否成立?为什么?
AB+AC>BC
BA+BC>AC
CA+CB>AB
三角形任意两边的和大于第三边。
随堂练习
1.用同样长度的小棒搭成如右图所示的形状,一共用了几根小棒?有多少个三角形?
9根小棒
5个三角形
2.用同样长度的小棒(火柴棒或牙签)3根、4根、5根、6根、7根、8根……搭三角形,把搭的结果填在表格里。
小棒根数
3
4
5
6
7
8
能否搭成三角形
能
不能
能
不能
能
不能
搭成三角形的个数
1
2
3
三角形的类型
等边
等边
等边
下列长度的各组线段,能构成三角形的是:
A.
5cm、4cm、3cm
B.
9cm、5cm、4cm
C.
7cm、4cm、2cm
答:A
知识巩固
从A点到B点,最短的路径是哪一条?若要与过C点的路径比较,谁的路程远呢?
A
B
C
根据线段的基本性质有:AB<AC+BC
20.三角形的角
三个角都是锐角的三角形叫做锐角三角形。
有一个角是钝角的三角形叫做钝角三角形。
别忘了还有直角三角形。
有一个角是直角的三角形叫做直角三角形。
三角形按角分
锐角三角形
钝角三角形
直角三角形
(3个角都是锐角的三角形)
(有1个角是直角的三角形)
(有1个角是钝角的三角形)
A
B
C
}
}
直角三角形
锐角三角形
钝角三角形
开动你的大脑思考下
△ABC的顶点A在直线上运动,可以形成哪些三角形?
21.三角形内角和
所有三角形的内角和都是180度吗?
?
所有三角形的内角和都是180度!
那我们来看看怎样来解题呢。
解法一:
解法二:
1、在△ABC中,∠C=78°,∠B=44°,求∠A。
∠A=180°-78°-44°
=102°-44°
=58°
∠A=180°-(78°+44°)
=180°-122°
=58°
2、等腰直角三角形的两个底角各是多少度?
∠B=∠A
=(180°-90°)÷2
=45°
A
B
C
一个直角三角形中最多有( )个直角,
为什么?
一个钝角三角形中最多有( )个钝角,
为什么?
练一练
1
1
1、填空
2、一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
180°-70°×2
180°-70°
-70°
70°
70°
40°
内角和180°
180°-90°-50°=40°
180°-(50°+90°)=40°
3、一个直角三角形,一个锐角是50°,另一个锐角是几度?
50°
90°-50°=40°
?
A、比90°小
B、比90°大
C、可能等于90°,大于90°或小于90°
D、还是180°
①把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和(
)
D
拓展训练
A.一定是锐角
B.一定是钝角
C.一定是直角
D.可能是锐角或钝角或直角。
②一个三角形,有两个角是锐角,则第三个角(
)
D
判断
(1)三角形的内角和是180°。(
)
(2)钝角三角形的内角和比锐角三角形的大。(
)
(3)三角形越大,它的内角和就越大。(
)
√
×
×
22.平行四边形的边与角
像这样两组对边分别平行的四边形叫做平行四边形。
(1)
(2)
(3)
(4)
(5)
(6)
长方形和正方形的两组对边都互相平行。
那么我们再看看下列图形中哪些是平行四边形?
所以:长方形和正方形它们都是特殊的平行四边形。
我还可以用图形表示长方形、正方形和平行四边形的关系。
平行四边形
长方形
正方形
你可以想到什么?
两组对边分别相等。
例、像右图那样,从长方形中剪下一个直角三角形,把它平移到另一侧,可以拼成一个平行四边形。
例、剪一些平行四边形
把它们的对角线分别重叠起来,重叠∠A,∠C。重叠∠B,∠D。
你会有什么发现?
两组对角分别相等。
练一练
特征
平行四边形
长方形
正方形
对边平行
对边相等
四边相等
对角相等
四个角都是直角
1、根据平行四边形、长方形、正方形的特征在
里画√。
√
√
√
√
√
√
√
√
√
√
√
√
2、把点与点连接起来,画出两个面积不等的平行四边形。
3、下面每组两个图形的大小有什么关系?剪一剪,拼一拼,想一想。
1、下面图形中是平行四边形的打上“√”。
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
√
√
√
√
2
3
4
5
6
7
8
拓展练习
1
2、填空题:
平行四边形的对边(
)而且(
),对角(
)。
平行
相等
相等
23.梯形的边与角
构成的图形是哪一类四边形?
只有一组对边平行的四边形叫做梯形。
我们把只有一组对边平行的四边形叫做梯形。
上底
下底
腰
腰
互相平行的一组对边分别叫做梯形的上底和下底,
不平行的一组对边叫做梯形的腰。
判断下面图形哪些是梯形,是的和不是都说出理由。
是
是
1.生活中你在哪些地方见过梯形呢?
梯子
沟渠横截面
堤坝横截面
2.思考一下
把长方形像右图那样剪开,就得到了两个梯形。
想一想,这是为什么?
腰相等
腰相等
3.用彩色笔画出下面梯形的腰,两腰相等吗?你是怎样发现的?
两腰相等的梯形叫做等腰梯形。
(1)观察下面梯形,它们的角有什么特别的地方?
梯形②和④中有直角。
像这样有直角的梯形叫做直角梯形。
4.
(2)观察下面梯形,它们的角有什么特别的地方?
上图中哪些是等腰梯形?
①和③
上底
下底
腰
腰
其中哪些角相等?
1
2
3
4
∠1=∠2
∠3=∠4
把点与点连接起来,画出两个形状不同的梯形。
练一练
找出下图中的梯形,并指出梯形的上底、下底和高。
平行四边形
梯形
梯形
梯形
下底
上底
上底
下底
上底
下底
拓展练习
24.图形的高与底
1、从三角形的一个顶点向它的对边作一条垂线,顶点和垂足间的线段叫做三角形的高,
三角形的高
这条对边叫做三角形的底。
底
三角形的高
底
2、从平行四边形一条边上的一点向对边作一条垂线,
平行四边形的高
这个点和垂足间的线段叫做平行
四边形的高,
这条对边叫做平行四边形的底。
底
高
底
3、从梯形上底的一点向下底作一条垂线,
这个点和垂足间的线段叫做梯形的高。
高
高
高
底
4、画三角形的高:先把三角尺的一条直角边与三角形的某一条边重合,另一条直角边平移到三角形的顶点,从这个顶点沿着三角尺的直角边向该线画垂线,这条垂线就是三角形这条边上的高。
练一练:
1、根据三角形的底,用三角尺画出他们的高。
底
高
底
高
底
高
2、根据平行四边形的底,用三角尺画出他们的高。
底
高
底
高
底
高
3、描出梯形的高。
下底
上底
上底
下底
下底
上底
1、判断下面的蓝色线段是平行四边形的底和高吗?是的话,哪条是底,哪条是高?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
拓展练习:
2、画出每个三角形底边上的高。
底
底
高
高
高
底
谢
谢
同课章节目录
- 一 自然数与整数
- 1.自然数
- 2.认识负数
- 3.整除
- 4.能被2,5整除的数
- 5.能被3整除的数
- 6.倍数与因数
- 7.素数与合数
- 8.分解因数
- 二 可能性
- 9.认识可能性
- 三 分数与除法
- 10.分数与除法的关系
- 11.一个数是另一个数的几分之几
- 12.真分数与假分数
- 13.假分数与整数
- 14.假分数与带分数
- 四 几何小天地
- 15.角的度量
- 16.角的分类
- 17.轴对称图形
- 18.图形的旋转
- 19.三角形的边
- 20.三角形的角
- 21.三角形内角和
- 22.平行四边形的边与角
- 23.梯形的边与角
- 24.图形的高与底
- 五 代数式与方程
- 25.代数式(一)
- 26.代数式(二)
- 27.认识方程
- 28.等式的性质
- 29.解方程
- 30.列方程解题(一)
- 31.列方程解题(二)
- 六 总复习
