《探索三角形全等条件（二）》PPT

(共15张PPT)
义务教育课程标准实验教科书（北师大版）七年级下册
第五章第4节（第2课时）
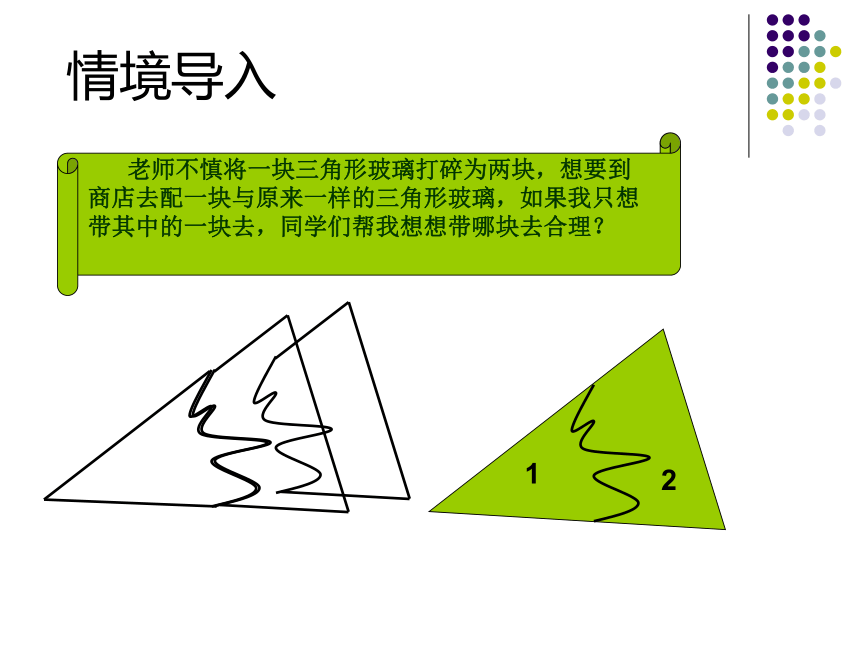
情境导入
老师不慎将一块三角形玻璃打碎为两块，想要到商店去配一块与原来一样的三角形玻璃，如果我只想带其中的一块去，同学们帮我想想带哪块去合理？
1
2
做一做
如果“两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60 和80 ，它们所夹的边为5cm，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？
60
80
5cm
60
判定条件2：
两角和它们的夹边对应
相等的两个三角形全等，
简写成“角边角”或“ASA”
判定条件3：
两角和其中一角的对边对应
相等的两个三角形全等，
简写成“角角边”或“AAS”
例题讲解
例1、如图，AB＝AC，∠B＝∠C，你能证明△ABD≌△ACE吗？
证明： △ABD和△ACE中
∠ =∠ （已知）
= （已知）
∠ =∠ （公共角）
∴ ≌ （ ）
B
C
AB
AC
A
A
△ABD
△ACE
ASA
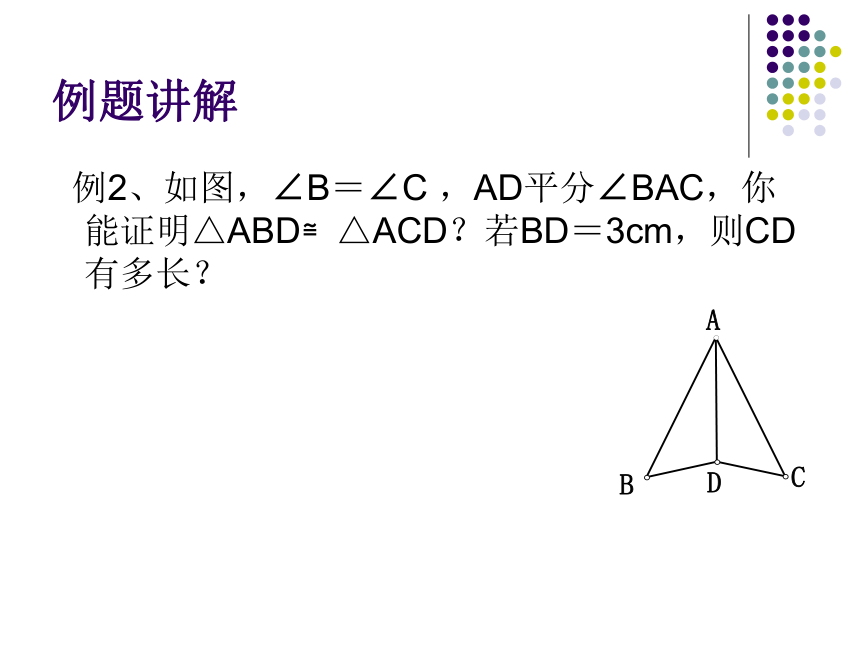
例题讲解
例2、如图，∠B＝∠C ，AD平分∠BAC，你能证明△ABD≌△ACD？若BD＝3cm，则CD有多长？
例题讲解
例3、如图，在△ABC中，BE⊥AD于E，CF⊥AD于F，且BE＝CF，那么BD与DC相等吗？你能说明理由吗？
双基巩固
1、如图，若AB=DE，∠A=∠D,∠B=∠E,则可判断△ABC≌△DEF,根据是 。
A
B
C
E
F
D
ASA
双基巩固
2、如图，已知AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO=DO吗？
证明：∵AD∥BC（已知）
∴∠A= ，（ ）
∠D= ，（ ）
在 中，
∴ ≌ （ ）
∴BO=DO（ ）
∠C
两直线平行，内错角相等
∠B
两直线平行,内错角相等
△AOD和△COB
△AOD
△COB
∠A=∠C(已知)
AD=BC (已知)
∠D=∠B(已知)
ASA
全等三角形的对应边相等
课堂小结：
本节课我们经历了对符合两角一边的条件的三角形进行画图验证，探索出三角形全等的另两个条件，它们分别是：　　　　
1）两角和它们的夹边对应相等的两个三角形全等（ASA）；
2）两角和其中一角的对边对应相等的两个三角形全等（AAS）。
再加上前面学的（SSS），证明两个三角形全等共有三个条件，我们要学会根据题目给出的已知选用合适的条件来证明两个三角形全等。
课后思考
如图，AB∥CD，∠A＝∠D，BF＝CE，∠AEB＝110°，求∠DFC的度数。
解：∵AB∥CD(已知)
∴∠B=∠C(两直线平行，内错角相等)
∵BF=CE(已知)
∴BF－EF=CE－EF
∴BE=CF
在△ABE和△DCF中
∠B=∠C(已知)
∠A=∠D(已知)
BE=CF(已知)
∴△ ABE≌△DCF(AAS)
∴∠DFC=∠AEB=110 (全等三角形的对应角相等)
°
作业布置
1、课本164页，习题5.8知识技能1、2、3题
2、预习教材165页—166页。