12.2.3 全等三角形的判定AAS,ASA课时达标(含答案)
文档属性
| 名称 | 12.2.3 全等三角形的判定AAS,ASA课时达标(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2.3全等三角形的判定AAS,ASA课时达标
一、选择题
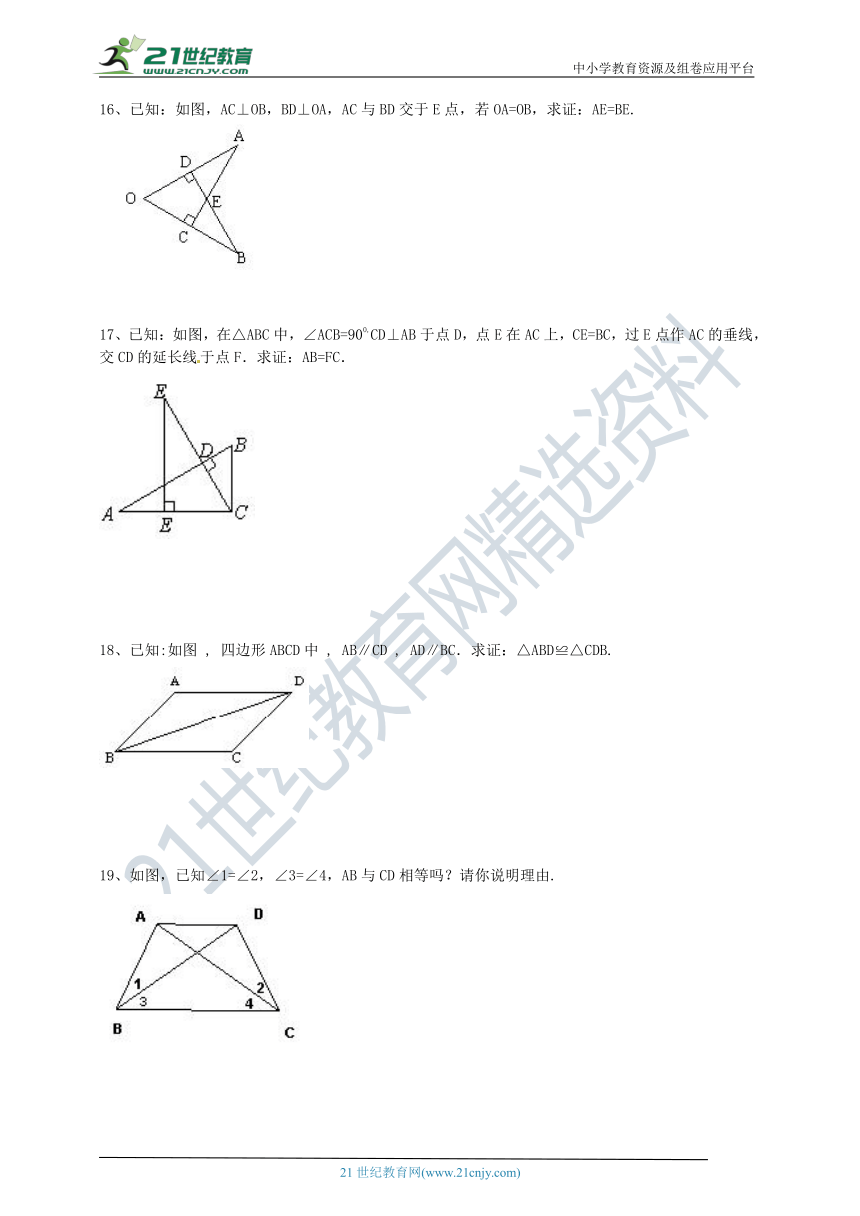
1、要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是(??
)
A.SSS????????
?
B.ASA???????
?
C.SAS??????
???
D.HL
2、小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
A.第1块????
B.第2块????
C.第3块????
D.第4块
3、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是(
??)
A.甲和乙?
B.乙和丙?
C.只有乙?
D.只有丙
4、如图,已知AB=AD,使用“ASA”能直接判定△ABC≌△ADE的是(
)
A.∠B=∠C????
B.AC=AD?????
C.BC=DE???????
D.∠ACB=∠AED
5、如图,已知∠ADB=∠ADC,欲证△ABD≌△ACD,还必须从下列选项中选一个补充条件,其中错误的选项是( )
A.∠BAD=∠CAD?
??
B.AB=AC???????C.BD=CD????
D.∠B=∠C
6、如图,已知△ABC中,∠ABC=450,AC=4,H是高AD和BE的交点,则线段BH的长度为(???
)
A.2???????
B.4???????
C.5???????????
D.不能确定
?
7、如图所示,已知D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC∥AB,若BD=2,CF=5,则AB的长为(
)
A.1
B.3
C.5
D.7
8、如图,请看以下两个推理过程:
①∵∠D=∠B,∠E=∠C,DE=BC,
∴△ADE≌△ABC(AAS);
②∵∠DAE=∠BAC,∠E=∠C,DE=BC,∴△ADE≌△ABC(AAS).
则以下判断正确的(包括判定三角形全等的依据)是( ).
A.①对②错?
B.①错②对
C.①②都对?
D.①②都错
二、填空题
9、如下图,Rt△ABC和Rt△DEF,∠C=∠F=90°
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是__________.
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是__________.
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是__________.
(4)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是__________.
10、如图
,
AC⊥BC于C
,
DE⊥AC于E
,
AD⊥AB于A
,
BC=AE.若AB=5
,
则AD=___________。
?
11、如图,点B、E、F、C在同一直线上.
已知∠A
=∠D,∠B
=∠C,要使△ABF≌△DCE,需要补充的一个条件是???????
(写出一个即可).
12、如图,∠E=∠F=900,∠B=∠C,AE=AF。给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论是?????????
(填序号)。
13、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ。则下列结论:①
AD=BE;②
PQ∥AE;③
AP=BQ;④
DE=DP。其中正确的是???
??????????????。
三、解答题
14、如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:AE=CF.
15、已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B求证:△ABC≌△CDE
16、已知:如图,AC⊥OB,BD⊥OA,AC与BD交于E点,若OA=OB,求证:AE=BE.
?
17、已知:如图,在△ABC中,∠ACB=900,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.求证:AB=FC.
?
18、已知:如图
,
四边形ABCD中
,
AB∥CD
,
AD∥BC.求证:△ABD≌△CDB.
19、如图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
20、如图,给出五个等量关系:①AD=BC、②AC=BD、③CE=DE、④∠D=∠C、⑤∠DAB=∠CBA.
请你以其中两个为条件,另三个中的一个为结论,推出一个正确的命题(只需写出一种情况),并加以证明.
已知:
求证:
证明:
?
21、已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC求证:BC=DE
22、在△ABC中,∠ABC=900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E;
(1)当直线MN绕点C旋转到图甲的位置时,
求证:(1)△ADC≌CEB;(2)DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明。
参考答案
一、选择题
1、B???????
????????????
2、B解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:B.
3、B
4、a
5、B解:A、∵∠ADB=∠ADC,∠BAD=∠CAD,AD=AD,利用ASA可以证明△ABD≌△ACD,正确;
B、∵∠ADB=∠ADC,AD=AD,AB=AC,不能证明△ABD≌△ACD,错误;
C、∵∠ADB=∠ADC,AD=AD,BD=CD,利用SAS能证明△ABD≌△ACD,正确;
D、∵∠ADB=∠ADC,∠B=∠C,AD=AD,利用AAS可以证明△ABD≌△ACD,正确;
6、B
7、D
8、B 点拨:①中的判定根据为ASA,不是AAS,①错误;②是正确的.故选B.
二、填空题
三、解答题
14、证明:∵AB∥CD,
∴∠B=∠D(两直线平行,内错角相等)
又∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(ASA)
∴AE=CF(全等三角形对应边相等)????
15、证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E?
又∵∠ACD=∠B,
∴∠B=∠D???????????
又∵AC=CE,
∴△ABC≌△CDE
16、证明:∵AC⊥OB,BD⊥OA,∴∠ODB=∠OCA=90°
∴在△OCA和△ODB中
∵OA=OB,∠ODB=∠OCA,∠O=∠O
∴△OCA≌△ODB(AAS)
∴OD=OC
∴AD=BC
在△ADE和△BCE中
∵DA=CB,∠ADE=∠BCE,∠AED=∠BEC
∴△ADE≌△BCE(AAS)
∴AE=BE
17、证明:∵
FE⊥AC于点E,
∠ACB=90°,
∴
∠FEC
=∠ACB=90°.
∴
∠F+∠ECF=90°.
又∵
CD⊥AB于点D,
∴
∠A+∠ECF=90°
.
∴
∠A=∠F
.??
在△ABC和△FCE中,
∴
△ABC≌△FCE.
∴
AB=FC
.
18、∵AB∥CD
,
AD∥BC
∴∠ABD=∠CDB,
∠ADB=∠CBD
又∵BD=DB
∴△ABD≌△CDB.
19、解:AB=CD,理由如下:
?
∵∠1=∠2,,∠3=∠4
?
∴∠1+∠3=∠2+∠4
?
∴∠ABC=∠DCB
?
又∵
BC=CB
?
∴△ABC≌△DCB(ASA)
?
∴
AB=CD
20、情况一:已知:AD=BC,AC=BD
求证:CE=DE(或∠D=∠C或∠DAB=∠CBA)
证明:在△ABD和△BAC中
∴△ABD≌△BAC
??
即CE=ED.
情况二:已知:∠D=∠C或∠DAB=∠CBA
求证:AD=BC(或AC=BD或CE=DE)
证明:在△ABD和△BAC中
∠D=∠C,∠DAB=∠CBA
∵AB=AB
∴△ABD≌△BAC
∴AD=BC.
21、证明:∵AB∥EC,
?
∴∠A=∠DCE??
?
在△ABC和△CDE中,
∴△ABC≌△CDE.
∴BC=DE????
?
22、证明:(1)①
???
???
???
???
②
???
???
???
(2)
???
???
又
???
???
(3)当MN旋转到图丙的位置时,AD、DE、BE所满足的等量关系是DE=BE-AD
(或AD=BE-DE,BE=AD+DE等)
?
?
???
又∵AC=BC
???
???
???
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2.3全等三角形的判定AAS,ASA课时达标
一、选择题
1、要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是(??
)
A.SSS????????
?
B.ASA???????
?
C.SAS??????
???
D.HL
2、小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
A.第1块????
B.第2块????
C.第3块????
D.第4块
3、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是(
??)
A.甲和乙?
B.乙和丙?
C.只有乙?
D.只有丙
4、如图,已知AB=AD,使用“ASA”能直接判定△ABC≌△ADE的是(
)
A.∠B=∠C????
B.AC=AD?????
C.BC=DE???????
D.∠ACB=∠AED
5、如图,已知∠ADB=∠ADC,欲证△ABD≌△ACD,还必须从下列选项中选一个补充条件,其中错误的选项是( )
A.∠BAD=∠CAD?
??
B.AB=AC???????C.BD=CD????
D.∠B=∠C
6、如图,已知△ABC中,∠ABC=450,AC=4,H是高AD和BE的交点,则线段BH的长度为(???
)
A.2???????
B.4???????
C.5???????????
D.不能确定
?
7、如图所示,已知D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC∥AB,若BD=2,CF=5,则AB的长为(
)
A.1
B.3
C.5
D.7
8、如图,请看以下两个推理过程:
①∵∠D=∠B,∠E=∠C,DE=BC,
∴△ADE≌△ABC(AAS);
②∵∠DAE=∠BAC,∠E=∠C,DE=BC,∴△ADE≌△ABC(AAS).
则以下判断正确的(包括判定三角形全等的依据)是( ).
A.①对②错?
B.①错②对
C.①②都对?
D.①②都错
二、填空题
9、如下图,Rt△ABC和Rt△DEF,∠C=∠F=90°
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是__________.
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是__________.
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是__________.
(4)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是__________.
10、如图
,
AC⊥BC于C
,
DE⊥AC于E
,
AD⊥AB于A
,
BC=AE.若AB=5
,
则AD=___________。
?
11、如图,点B、E、F、C在同一直线上.
已知∠A
=∠D,∠B
=∠C,要使△ABF≌△DCE,需要补充的一个条件是???????
(写出一个即可).
12、如图,∠E=∠F=900,∠B=∠C,AE=AF。给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论是?????????
(填序号)。
13、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ。则下列结论:①
AD=BE;②
PQ∥AE;③
AP=BQ;④
DE=DP。其中正确的是???
??????????????。
三、解答题
14、如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:AE=CF.
15、已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B求证:△ABC≌△CDE
16、已知:如图,AC⊥OB,BD⊥OA,AC与BD交于E点,若OA=OB,求证:AE=BE.
?
17、已知:如图,在△ABC中,∠ACB=900,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.求证:AB=FC.
?
18、已知:如图
,
四边形ABCD中
,
AB∥CD
,
AD∥BC.求证:△ABD≌△CDB.
19、如图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
20、如图,给出五个等量关系:①AD=BC、②AC=BD、③CE=DE、④∠D=∠C、⑤∠DAB=∠CBA.
请你以其中两个为条件,另三个中的一个为结论,推出一个正确的命题(只需写出一种情况),并加以证明.
已知:
求证:
证明:
?
21、已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC求证:BC=DE
22、在△ABC中,∠ABC=900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E;
(1)当直线MN绕点C旋转到图甲的位置时,
求证:(1)△ADC≌CEB;(2)DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明。
参考答案
一、选择题
1、B???????
????????????
2、B解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:B.
3、B
4、a
5、B解:A、∵∠ADB=∠ADC,∠BAD=∠CAD,AD=AD,利用ASA可以证明△ABD≌△ACD,正确;
B、∵∠ADB=∠ADC,AD=AD,AB=AC,不能证明△ABD≌△ACD,错误;
C、∵∠ADB=∠ADC,AD=AD,BD=CD,利用SAS能证明△ABD≌△ACD,正确;
D、∵∠ADB=∠ADC,∠B=∠C,AD=AD,利用AAS可以证明△ABD≌△ACD,正确;
6、B
7、D
8、B 点拨:①中的判定根据为ASA,不是AAS,①错误;②是正确的.故选B.
二、填空题
三、解答题
14、证明:∵AB∥CD,
∴∠B=∠D(两直线平行,内错角相等)
又∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(ASA)
∴AE=CF(全等三角形对应边相等)????
15、证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E?
又∵∠ACD=∠B,
∴∠B=∠D???????????
又∵AC=CE,
∴△ABC≌△CDE
16、证明:∵AC⊥OB,BD⊥OA,∴∠ODB=∠OCA=90°
∴在△OCA和△ODB中
∵OA=OB,∠ODB=∠OCA,∠O=∠O
∴△OCA≌△ODB(AAS)
∴OD=OC
∴AD=BC
在△ADE和△BCE中
∵DA=CB,∠ADE=∠BCE,∠AED=∠BEC
∴△ADE≌△BCE(AAS)
∴AE=BE
17、证明:∵
FE⊥AC于点E,
∠ACB=90°,
∴
∠FEC
=∠ACB=90°.
∴
∠F+∠ECF=90°.
又∵
CD⊥AB于点D,
∴
∠A+∠ECF=90°
.
∴
∠A=∠F
.??
在△ABC和△FCE中,
∴
△ABC≌△FCE.
∴
AB=FC
.
18、∵AB∥CD
,
AD∥BC
∴∠ABD=∠CDB,
∠ADB=∠CBD
又∵BD=DB
∴△ABD≌△CDB.
19、解:AB=CD,理由如下:
?
∵∠1=∠2,,∠3=∠4
?
∴∠1+∠3=∠2+∠4
?
∴∠ABC=∠DCB
?
又∵
BC=CB
?
∴△ABC≌△DCB(ASA)
?
∴
AB=CD
20、情况一:已知:AD=BC,AC=BD
求证:CE=DE(或∠D=∠C或∠DAB=∠CBA)
证明:在△ABD和△BAC中
∴△ABD≌△BAC
??
即CE=ED.
情况二:已知:∠D=∠C或∠DAB=∠CBA
求证:AD=BC(或AC=BD或CE=DE)
证明:在△ABD和△BAC中
∠D=∠C,∠DAB=∠CBA
∵AB=AB
∴△ABD≌△BAC
∴AD=BC.
21、证明:∵AB∥EC,
?
∴∠A=∠DCE??
?
在△ABC和△CDE中,
∴△ABC≌△CDE.
∴BC=DE????
?
22、证明:(1)①
???
???
???
???
②
???
???
???
(2)
???
???
又
???
???
(3)当MN旋转到图丙的位置时,AD、DE、BE所满足的等量关系是DE=BE-AD
(或AD=BE-DE,BE=AD+DE等)
?
?
???
又∵AC=BC
???
???
???
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
