12.2.4 全等三角形的判定HL课时达标(含答案)
文档属性
| 名称 | 12.2.4 全等三角形的判定HL课时达标(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 17:44:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
12.2.4全等三角形的判定HL课时达标
一、选择题
1、下列条件中,能判定两个直角三角形全等的是(??
)
A.一锐角对应相等???????????????B.两锐角对应相等?
C.一条边对应相等???????????????D.两条直角边对应相等
2、在△ABC和△DEF中,∠A=∠D=90°,则下列条件不能判定△ABC和△DEF全等的是(???
)
A.AB=DE,AC=DF
?
B.AC=EF,BC=DF
C.AB=DE,BC=EF?
D.∠C=∠F,BC=EF
3、如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是(
)
A.∠C=∠B????????????
B.DF∥AE????????????????
C.∠A+∠D=90°???
D.CF=BE
4、如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(???
)
A.SSS?????
B.ASA
C.SSA?????????D.HL
5、如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,AC=6,EC=6,∠ACB=60°,则∠ACD的度数为(
)
A.45°
B.30°
C.20°
D.15°
二、填空题
6、如图,Rt△AOB≌Rt△CDA,且A(-1,0),B(0,2)则点C的坐标是_______。
7、如右图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△__________≌△__________,其判定依据是__________,还有△__________≌△__________,其判定依据是__________.
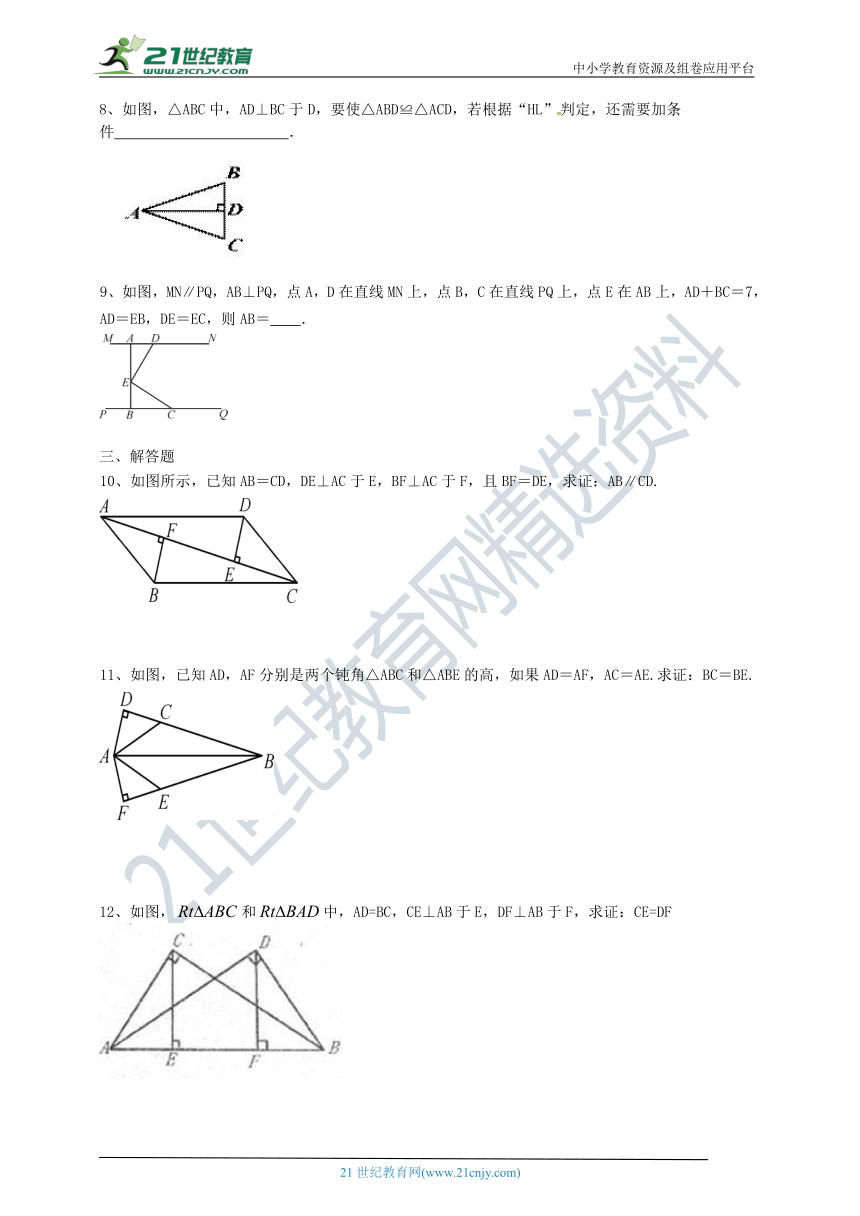
8、如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件???????
????.
?
9、如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=
.
三、解答题
10、如图所示,已知AB=CD,DE⊥AC于E,BF⊥AC于F,且BF=DE,求证:AB∥CD.
11、如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.
12、如图,和中,AD=BC,CE⊥AB于E,DF⊥AB于F,求证:CE=DF
?
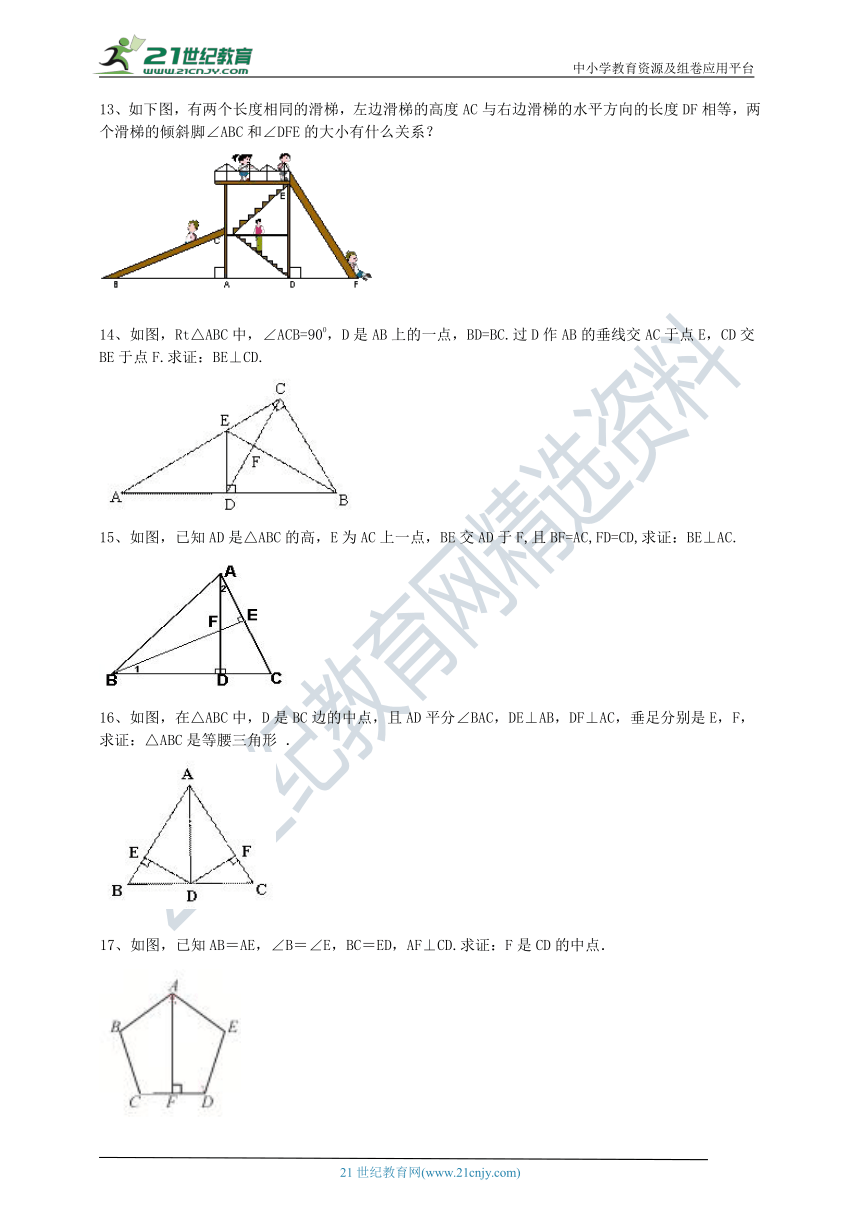
13、如下图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等,两个滑梯的倾斜脚∠ABC和∠DFE的大小有什么关系?
14、如图,Rt△ABC中,∠ACB=900,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.????
15、如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,求证:BE⊥AC.
16、如图,在△ABC中,D是BC边的中点,且AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别是E,F,求证:△ABC是等腰三角形
.
17、如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:F是CD的中点.
参考答案
一、选择题
1、D
2、B
3、C解:∵CE=BF,
∴CE﹣EF=BF=EF,
∴CF=BE,
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△CFD和Rt△BEA中,,
∴Rt△CFD≌Rt△BEA(HL),
∴∠C=∠B,∠D=∠A,
∴CD∥AB,故A,B,D正确,
∵∠C+∠D=90°,
∴∠A+∠C=90°,故C错误,
故选:C.
4、D
5、B
二、填空题
6、(-3,1)
7、ABC?
DCB?
HL?
ABO?
DCO?
AAS
8、AB=AC
9、7
三、解答题
11、证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
∵AB=AB,AD=AF,
∴Rt△ABD≌Rt△ABF.
∴DB=FB.
∵AC=AE,AD=AF,
∴Rt△ADC≌Rt△AFE.
∴DC=FE.
∴DB-DC=FB-FE,即BC=BE.
12、证明:在和中,∠ACB=∠BDA=900.
???
,
???
,
???
;
???
在△BCE和△ADF中.
???
,
???
,
???
,
???
13、用HL证明Rt△BAC≌Rt△EDF
14、证明:∵ED⊥AB
∴∠EDB=900
在Rt△ECB和Rt△EDB中
∴Rt△ECB≌Rt△EDB(HL)
∴∠EBC=∠EBD
又BD=BC
∴BF⊥CD(三线合一)
∵
AD是△ABC的高???
∴∠ADB=∠ADC=90°
∵BF=AC,FD=CD??????
∴RT△BDF≌RT△ADC(HL)
∴∠1=∠2??
∵∠1+∠ADB=∠2+∠AEF??
∴∠AEF=90°?
∴BE⊥AC
16、证明:∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵D是BC边的中点,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDE(HL),
∴∠B=∠C.∴△ABC是等腰三角形
17、证明:连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2.4全等三角形的判定HL课时达标
一、选择题
1、下列条件中,能判定两个直角三角形全等的是(??
)
A.一锐角对应相等???????????????B.两锐角对应相等?
C.一条边对应相等???????????????D.两条直角边对应相等
2、在△ABC和△DEF中,∠A=∠D=90°,则下列条件不能判定△ABC和△DEF全等的是(???
)
A.AB=DE,AC=DF
?
B.AC=EF,BC=DF
C.AB=DE,BC=EF?
D.∠C=∠F,BC=EF
3、如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是(
)
A.∠C=∠B????????????
B.DF∥AE????????????????
C.∠A+∠D=90°???
D.CF=BE
4、如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(???
)
A.SSS?????
B.ASA
C.SSA?????????D.HL
5、如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,AC=6,EC=6,∠ACB=60°,则∠ACD的度数为(
)
A.45°
B.30°
C.20°
D.15°
二、填空题
6、如图,Rt△AOB≌Rt△CDA,且A(-1,0),B(0,2)则点C的坐标是_______。
7、如右图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△__________≌△__________,其判定依据是__________,还有△__________≌△__________,其判定依据是__________.
8、如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件???????
????.
?
9、如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=
.
三、解答题
10、如图所示,已知AB=CD,DE⊥AC于E,BF⊥AC于F,且BF=DE,求证:AB∥CD.
11、如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.
12、如图,和中,AD=BC,CE⊥AB于E,DF⊥AB于F,求证:CE=DF
?
13、如下图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等,两个滑梯的倾斜脚∠ABC和∠DFE的大小有什么关系?
14、如图,Rt△ABC中,∠ACB=900,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.????
15、如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,求证:BE⊥AC.
16、如图,在△ABC中,D是BC边的中点,且AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别是E,F,求证:△ABC是等腰三角形
.
17、如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:F是CD的中点.
参考答案
一、选择题
1、D
2、B
3、C解:∵CE=BF,
∴CE﹣EF=BF=EF,
∴CF=BE,
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△CFD和Rt△BEA中,,
∴Rt△CFD≌Rt△BEA(HL),
∴∠C=∠B,∠D=∠A,
∴CD∥AB,故A,B,D正确,
∵∠C+∠D=90°,
∴∠A+∠C=90°,故C错误,
故选:C.
4、D
5、B
二、填空题
6、(-3,1)
7、ABC?
DCB?
HL?
ABO?
DCO?
AAS
8、AB=AC
9、7
三、解答题
11、证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
∵AB=AB,AD=AF,
∴Rt△ABD≌Rt△ABF.
∴DB=FB.
∵AC=AE,AD=AF,
∴Rt△ADC≌Rt△AFE.
∴DC=FE.
∴DB-DC=FB-FE,即BC=BE.
12、证明:在和中,∠ACB=∠BDA=900.
???
,
???
,
???
;
???
在△BCE和△ADF中.
???
,
???
,
???
,
???
13、用HL证明Rt△BAC≌Rt△EDF
14、证明:∵ED⊥AB
∴∠EDB=900
在Rt△ECB和Rt△EDB中
∴Rt△ECB≌Rt△EDB(HL)
∴∠EBC=∠EBD
又BD=BC
∴BF⊥CD(三线合一)
∵
AD是△ABC的高???
∴∠ADB=∠ADC=90°
∵BF=AC,FD=CD??????
∴RT△BDF≌RT△ADC(HL)
∴∠1=∠2??
∵∠1+∠ADB=∠2+∠AEF??
∴∠AEF=90°?
∴BE⊥AC
16、证明:∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵D是BC边的中点,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDE(HL),
∴∠B=∠C.∴△ABC是等腰三角形
17、证明:连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
