13.1.2 线段的垂直平分线的性质第1课时课时达标(含答案)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质第1课时课时达标(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
13.1.2线段的垂直平分线的性质课时达标
第1课时:线段的垂直平分线的性质与判定
一、选择题
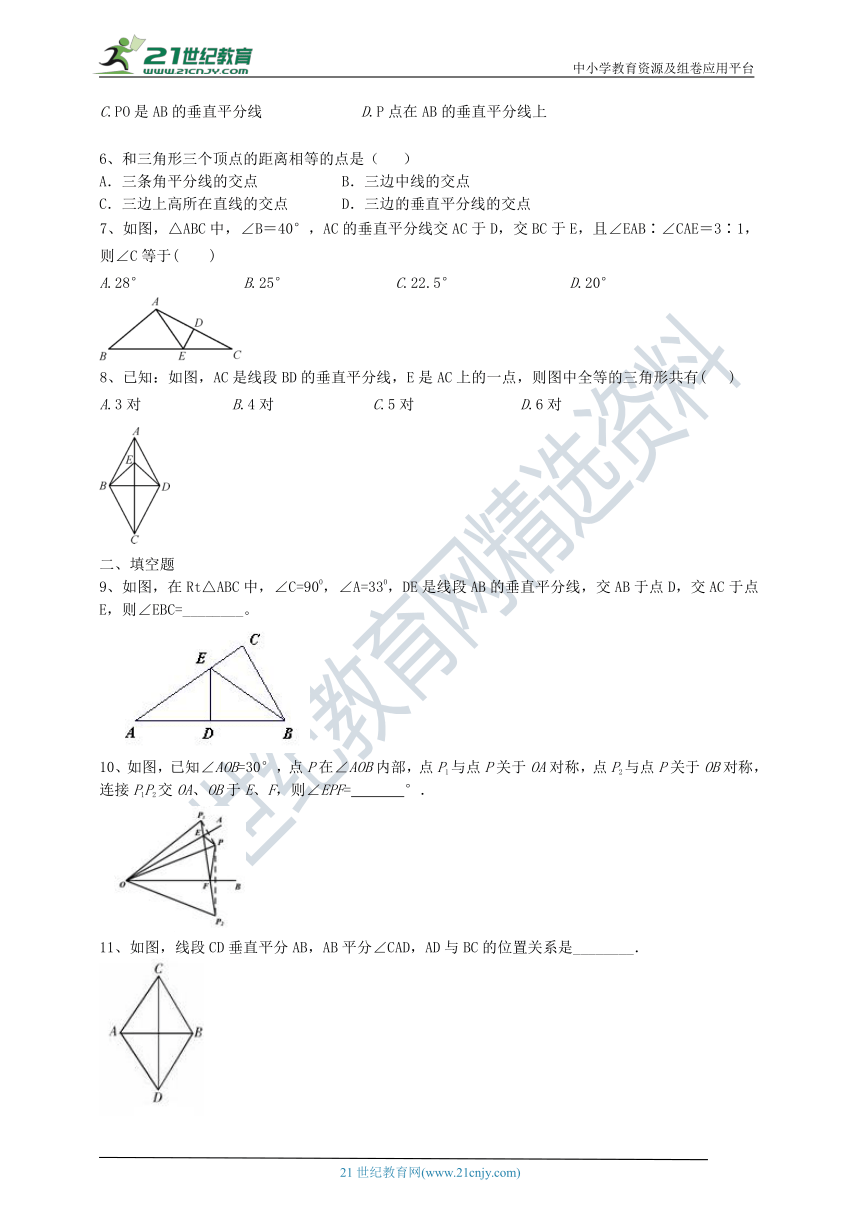
1、如图,△ABC的两边AC和BC的垂直平分线分别交AB于D、E两点,若AB边的长为10cm,则△CDE的周长为( )
A.10cm
B.20cm
C.5cm?
D.不能确定
2、在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是(??
)
A.15°??
?????
B.30°???
?????
C.50°???
??D.65°????
3、如图,Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点D,交BC于点E,AE平分∠BAC,那么下列关系式中不成立的是(???
)
A.∠B=∠CAE???
???
B.∠DEA=∠CEA
C.∠B=∠BAE????
D.AC=2EC
4、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于18cm,则AC的长等于(??
)
A.6
cm???
?
B.8
cm???
?
??
C.10
cm
??
??
D.12
cm
5、已知:如图,直线PO与AB交于O点,PA=PB.则下列结论中正确的是(
)
A.AO=BO
B.PO⊥AB
C.PO是AB的垂直平分线
D.P点在AB的垂直平分线上
6、和三角形三个顶点的距离相等的点是(?
)
A.三条角平分线的交点?????
B.三边中线的交点
C.三边上高所在直线的交点?
D.三边的垂直平分线的交点
7、如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于(
)
A.28°
B.25°
C.22.5°
D.20°
8、已知:如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有(
)
A.3对
B.4对
C.5对
D.6对
二、填空题
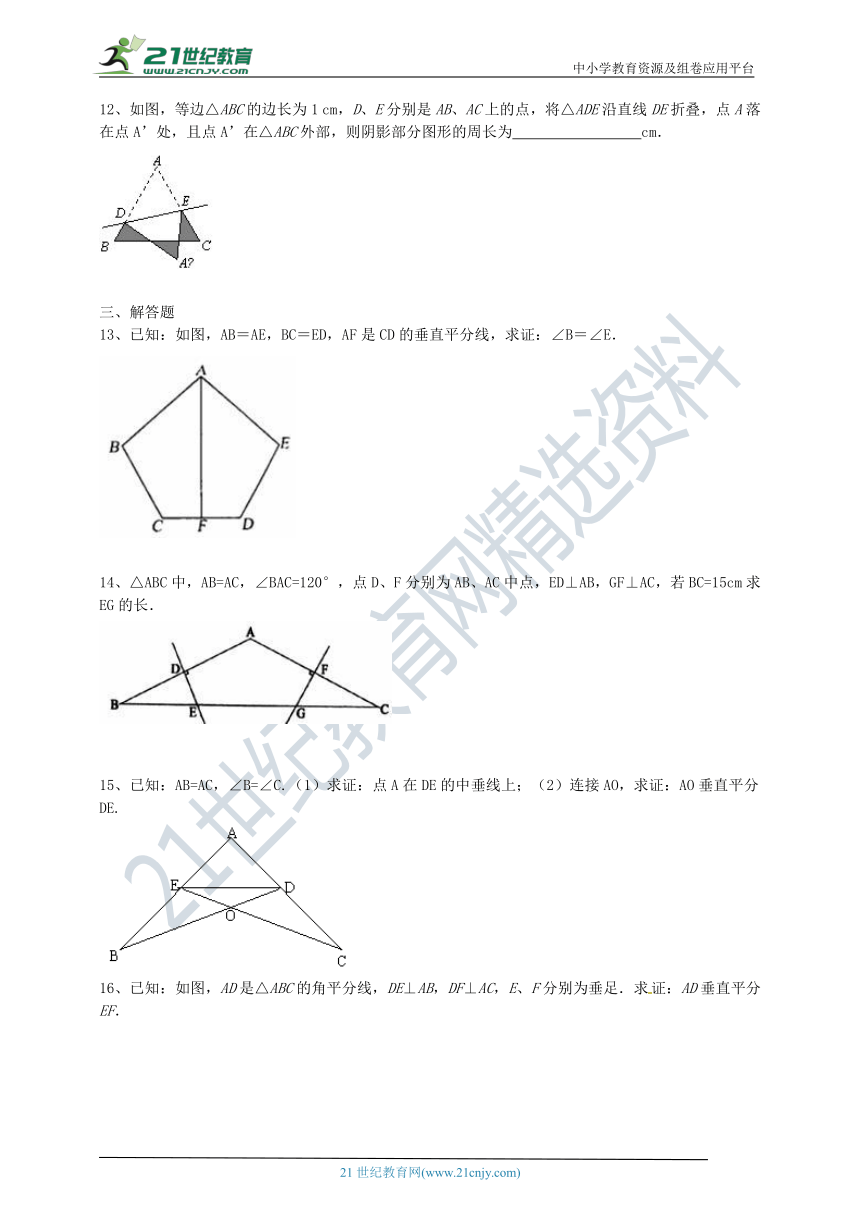
9、如图,在Rt△ABC中,∠C=900,∠A=330,DE是线段AB的垂直平分线,交AB于点D,交AC于点E,则∠EBC=________。
10、如图,已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,则∠EPF= ??
°.
11、如图,线段CD垂直平分AB,AB平分∠CAD,AD与BC的位置关系是________.
12、如图,等边△ABC的边长为1
cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A’处,且点A’在△ABC外部,则阴影部分图形的周长为???
?????cm.
三、解答题
13、已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.?
14、△ABC中,AB=AC,∠BAC=120°,点D、F分别为AB、AC中点,ED⊥AB,GF⊥AC,若BC=15cm求EG的长.
15、已知:AB=AC,∠B=∠C.(1)求证:点A在DE的中垂线上;(2)连接AO,求证:AO垂直平分DE.
16、已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,E、F分别为垂足.求证:AD垂直平分EF.
17、如图,点E是∠AOB的平分线上一点,EC⊥OA,
ED⊥OB,
垂足分别是C,D.
求证:(1)∠ECD
=∠EDC????
(2)
OC
=
OD???
(3)OE是线段CD的垂直平分线.
18、如图,已知△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
参考答案
一、选择题
1、A解:∵△ABC的两边BC和AC的垂直平分线分别交AB于D、E,
∴AD=CD,BE=CE,
∵边AB长为10cm,
∴△CDE的周长为:CD+DE+CE=AD+DE+BE=AB=10cm.
2、B
3、D
4、C
5、D
6、D
7、A
8、D
二、填空题
9、24°?????
10、120
11、互相平行
12、?3??
三、解答题
14、解:如图
?
连结AE、AG
?
∵AD为AB中点,ED⊥AB,∴EB=EA,∴△ABE为等腰三角形
?
?
又∵∠B=,∴∠BAE=30°,∴∠AEG=60°
?
?
同理可证:∠AGE=60°,∴△AEG为等边三角形,∴AE=EG=AG
?
?
又∵AE=BE,AG=GC,∴BE=EG=GC???
?
?
又BE+EG+GC=BC=15(cm)
???
∴EG=5(cm)
15、(1)证△ABD≌△ACE,∴AD=AE,∴A点在DE的中垂线上
???
(2)证EO=DO
???
∴O点在ED的中垂线上
???
∵A在DE的中垂线上
???
∴AO垂直平分DE
16、提示:由角平分线的性质定理,可得DE=DF,进而求得∠DEF=∠DFE,∠AEF=∠AFE,所以AE=AF,所以AD垂直平分EF.
17、解:(1)∠EDC与∠ECD相等??
∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB,
∴EC=ED?????????????
∴△CED是等腰三角形,
∴∠EDC=∠ECD????????
?
(2)OC与OD相等?????????
∵EC⊥OA,ED⊥OB,
∴∠ODE=∠OCE=90°?????????
在Rt△ODE和Rt△OCE中:OE=OE(公共边),DE=CE
∴Rt△ODE≌Rt△OCE(HL)
∴OD=OC
(3)OE是线段CD的垂直平分线
∵EC=ED,
∴E点在线段CD的垂直平分线上
∵OC=OD,
∴O点在线段CD的垂直平分线上
∴OE是线段CD的垂直平分线.
18、证明:(1)连接BE、CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
∵DE垂直平分BC,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
∴Rt△EFB≌Rt△EGC(HL).
∴BF=CG.
(2)∵BF=CG,
∴AB+AC=AB+BF+AG=AF+AG.
又易证Rt△AEF≌Rt△AEG(HL),
∴AF=AG.
∴AF=(AB+AC).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
13.1.2线段的垂直平分线的性质课时达标
第1课时:线段的垂直平分线的性质与判定
一、选择题
1、如图,△ABC的两边AC和BC的垂直平分线分别交AB于D、E两点,若AB边的长为10cm,则△CDE的周长为( )
A.10cm
B.20cm
C.5cm?
D.不能确定
2、在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是(??
)
A.15°??
?????
B.30°???
?????
C.50°???
??D.65°????
3、如图,Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点D,交BC于点E,AE平分∠BAC,那么下列关系式中不成立的是(???
)
A.∠B=∠CAE???
???
B.∠DEA=∠CEA
C.∠B=∠BAE????
D.AC=2EC
4、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于18cm,则AC的长等于(??
)
A.6
cm???
?
B.8
cm???
?
??
C.10
cm
??
??
D.12
cm
5、已知:如图,直线PO与AB交于O点,PA=PB.则下列结论中正确的是(
)
A.AO=BO
B.PO⊥AB
C.PO是AB的垂直平分线
D.P点在AB的垂直平分线上
6、和三角形三个顶点的距离相等的点是(?
)
A.三条角平分线的交点?????
B.三边中线的交点
C.三边上高所在直线的交点?
D.三边的垂直平分线的交点
7、如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于(
)
A.28°
B.25°
C.22.5°
D.20°
8、已知:如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有(
)
A.3对
B.4对
C.5对
D.6对
二、填空题
9、如图,在Rt△ABC中,∠C=900,∠A=330,DE是线段AB的垂直平分线,交AB于点D,交AC于点E,则∠EBC=________。
10、如图,已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,则∠EPF= ??
°.
11、如图,线段CD垂直平分AB,AB平分∠CAD,AD与BC的位置关系是________.
12、如图,等边△ABC的边长为1
cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A’处,且点A’在△ABC外部,则阴影部分图形的周长为???
?????cm.
三、解答题
13、已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.?
14、△ABC中,AB=AC,∠BAC=120°,点D、F分别为AB、AC中点,ED⊥AB,GF⊥AC,若BC=15cm求EG的长.
15、已知:AB=AC,∠B=∠C.(1)求证:点A在DE的中垂线上;(2)连接AO,求证:AO垂直平分DE.
16、已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,E、F分别为垂足.求证:AD垂直平分EF.
17、如图,点E是∠AOB的平分线上一点,EC⊥OA,
ED⊥OB,
垂足分别是C,D.
求证:(1)∠ECD
=∠EDC????
(2)
OC
=
OD???
(3)OE是线段CD的垂直平分线.
18、如图,已知△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
参考答案
一、选择题
1、A解:∵△ABC的两边BC和AC的垂直平分线分别交AB于D、E,
∴AD=CD,BE=CE,
∵边AB长为10cm,
∴△CDE的周长为:CD+DE+CE=AD+DE+BE=AB=10cm.
2、B
3、D
4、C
5、D
6、D
7、A
8、D
二、填空题
9、24°?????
10、120
11、互相平行
12、?3??
三、解答题
14、解:如图
?
连结AE、AG
?
∵AD为AB中点,ED⊥AB,∴EB=EA,∴△ABE为等腰三角形
?
?
又∵∠B=,∴∠BAE=30°,∴∠AEG=60°
?
?
同理可证:∠AGE=60°,∴△AEG为等边三角形,∴AE=EG=AG
?
?
又∵AE=BE,AG=GC,∴BE=EG=GC???
?
?
又BE+EG+GC=BC=15(cm)
???
∴EG=5(cm)
15、(1)证△ABD≌△ACE,∴AD=AE,∴A点在DE的中垂线上
???
(2)证EO=DO
???
∴O点在ED的中垂线上
???
∵A在DE的中垂线上
???
∴AO垂直平分DE
16、提示:由角平分线的性质定理,可得DE=DF,进而求得∠DEF=∠DFE,∠AEF=∠AFE,所以AE=AF,所以AD垂直平分EF.
17、解:(1)∠EDC与∠ECD相等??
∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB,
∴EC=ED?????????????
∴△CED是等腰三角形,
∴∠EDC=∠ECD????????
?
(2)OC与OD相等?????????
∵EC⊥OA,ED⊥OB,
∴∠ODE=∠OCE=90°?????????
在Rt△ODE和Rt△OCE中:OE=OE(公共边),DE=CE
∴Rt△ODE≌Rt△OCE(HL)
∴OD=OC
(3)OE是线段CD的垂直平分线
∵EC=ED,
∴E点在线段CD的垂直平分线上
∵OC=OD,
∴O点在线段CD的垂直平分线上
∴OE是线段CD的垂直平分线.
18、证明:(1)连接BE、CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
∵DE垂直平分BC,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
∴Rt△EFB≌Rt△EGC(HL).
∴BF=CG.
(2)∵BF=CG,
∴AB+AC=AB+BF+AG=AF+AG.
又易证Rt△AEF≌Rt△AEG(HL),
∴AF=AG.
∴AF=(AB+AC).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
