解不等式以及根的分布

(共16张PPT)
解不等式
二次函数根的分布
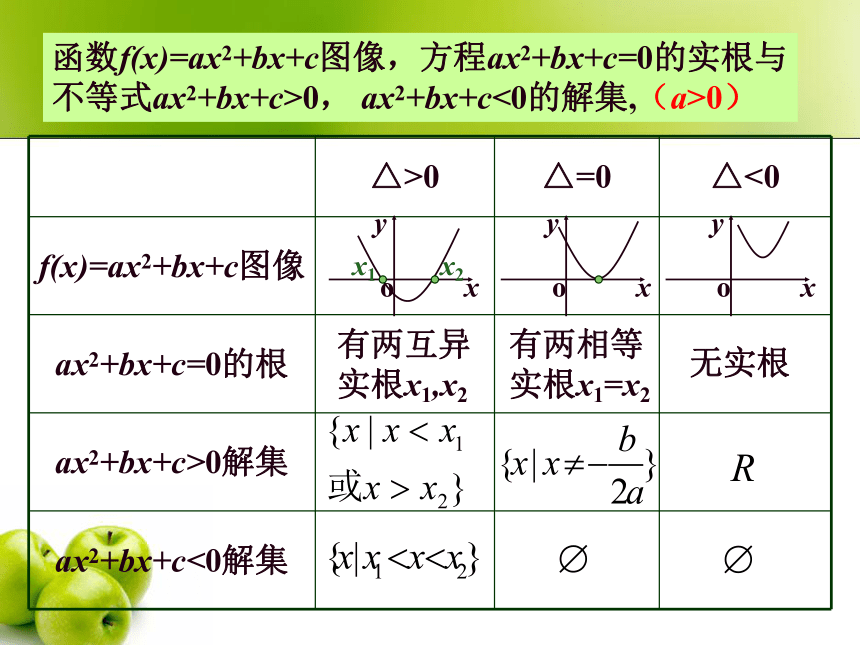
△>0 △=0 △<0
f(x)=ax2+bx+c图像
ax2+bx+c=0的根
ax2+bx+c>0解集
ax2+bx+c<0解集
o
x
y
有两互异
实根x1,x2
函数f(x)=ax2+bx+c图像，方程ax2+bx+c=0的实根与
不等式ax2+bx+c>0， ax2+bx+c<0的解集,（a>0）
o
x
y
有两相等
实根x1=x2
o
x
y
无实根
x1
x2
例1.解下列不等式：
解一元二次不等式的一般步骤：
(1)把二次项系数化为正数；
(2)解对应的一元二次方程的根；
(3)根据一元二次方程的根，结合不等号方向，
写出解集；
例2.解下列不等式：
小结：
例3.
练习：
二次函数根的分布
例1.已知方程x2+(m-2)x+(5-m)=0
的两根：
(1)都是正数； (2)一正一负；
(3)都大于2；
(4)一个根大于2，一个根小于2
分别m的取值范围.
根的分布 x1图像
等价条件
例1.已知方程x2+(m-2)x+(5-m)=0
的两根：
(1)都是正数； (2)一正一负；
(3)都大于2；
(4)一个根大于2，一个根小于2
分别m的取值范围.
练习：
巩固练习
已知关于x的方程3x2-5x+a=0的一根大于-2而小于0，另一根大于1而小于3，求实数a的范围
作业
《导与练》80页第8题；
82页第4，5，6题。
作业：
已知方程x2+(m-2)x+(5-m)=0的两根：
(1)都是正数； (2)一正一负；
(3)都大于2；
(4)一个根大于2，一个根小于2
分别求m的取值范围.