冲刺中考:几何图形中线段和差的最值问题
文档属性
| 名称 | 冲刺中考:几何图形中线段和差的最值问题 |

|
|
| 格式 | ppt | ||
| 文件大小 | 845.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-23 09:21:34 | ||
图片预览

文档简介
(共16张PPT)
几何图形中
线段和差的最值问题
冲刺中考
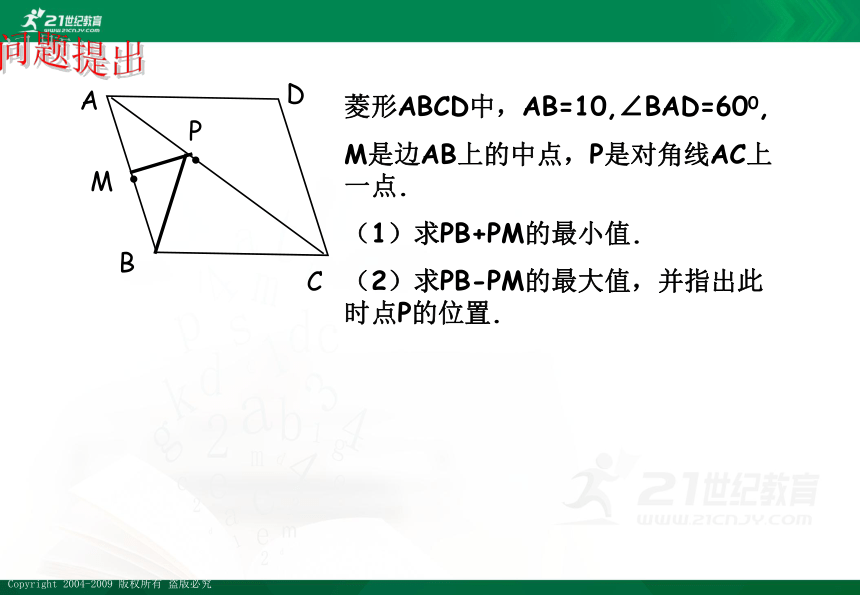
A
P
M
B
C
D
.
.
菱形ABCD中,AB=10,∠BAD=600,
M是边AB上的中点,P是对角线AC上一点.
(1)求PB+PM的最小值.
(2)求PB-PM的最大值,并指出此时点P的位置.
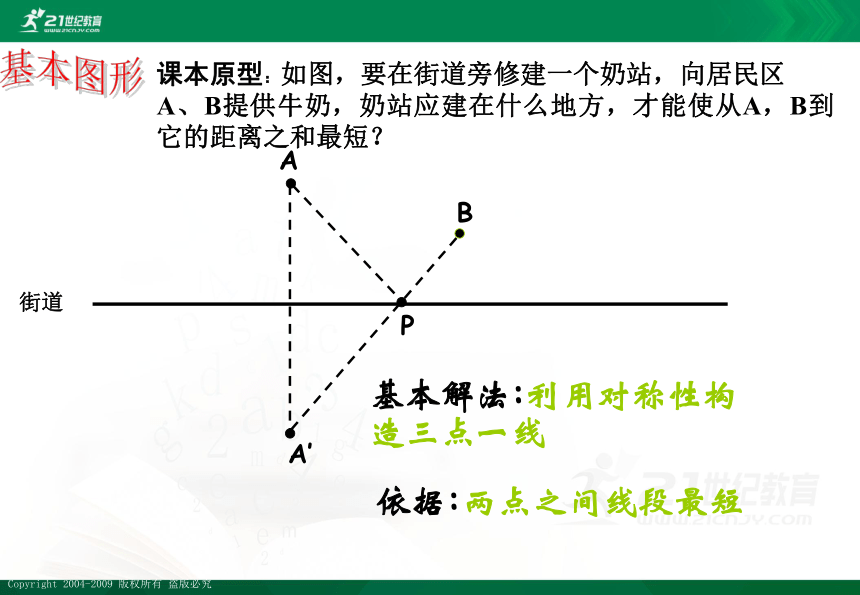
A
B
A’
P
课本原型:如图,要在街道旁修建一个奶站,向居民区 A、B提供牛奶,奶站应建在什么地方,才能使从A,B到它的距离之和最短?
街道
基本解法:利用对称性构 造三点一线
依据:两点之间线段最短
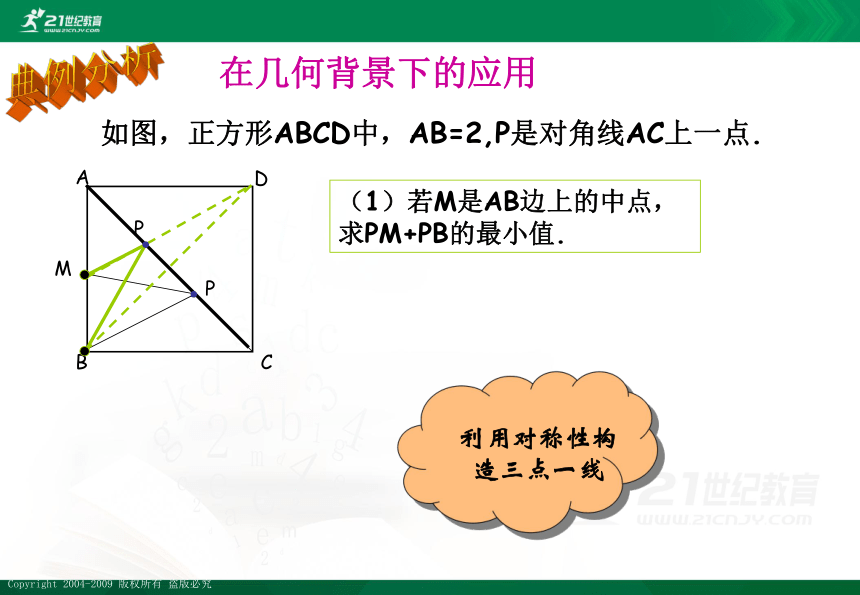
A
B
C
D
M
(1)若M是AB边上的中点,求PM+PB的最小值.
如图,正方形ABCD中,AB=2,P是对角线AC上一点.
P
P
利用对称性构造三点一线
在几何背景下的应用
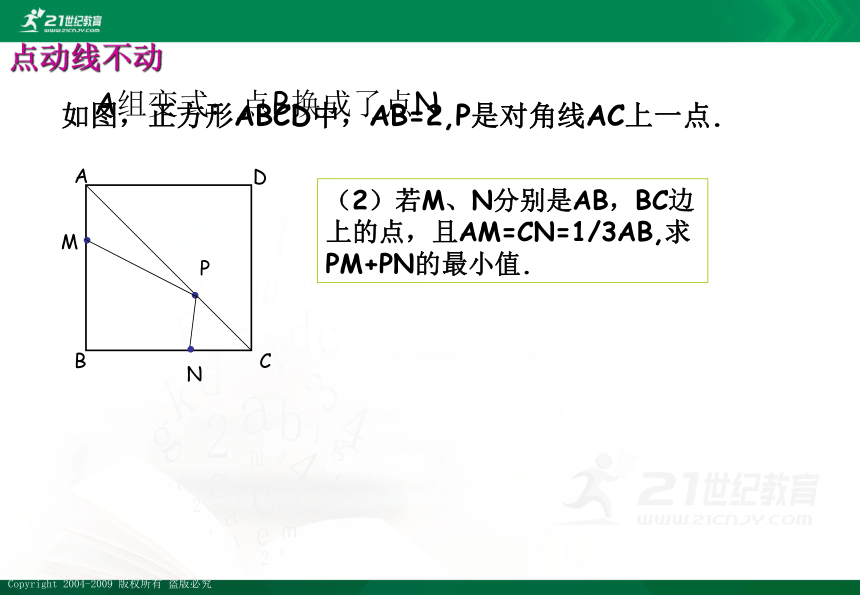
A
B
C
D
M
点动线不动
(2)若M、N分别是AB,BC边上的点,且AM=CN=1/3AB,求PM+PN的最小值.
P
N
A组变式:点B换成了点N
如图,正方形ABCD中,AB=2,P是对角线AC上一点.
A
B
C
D
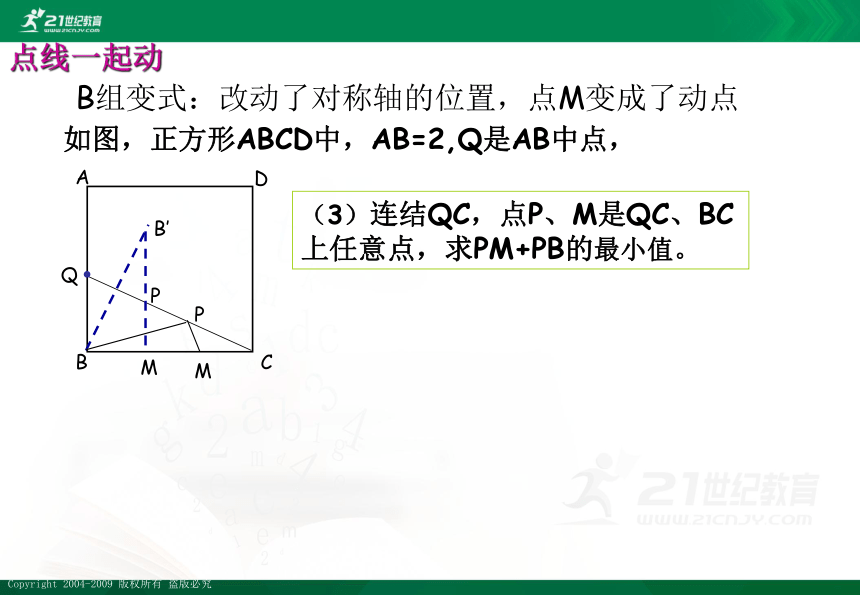
(3)连结QC,点P、M是QC、BC上任意点,求PM+PB的最小值。
B组变式:改动了对称轴的位置,点M变成了动点
如图,正方形ABCD中,AB=2,Q是AB中点,
Q
B’
M
P
点线一起动
P
M
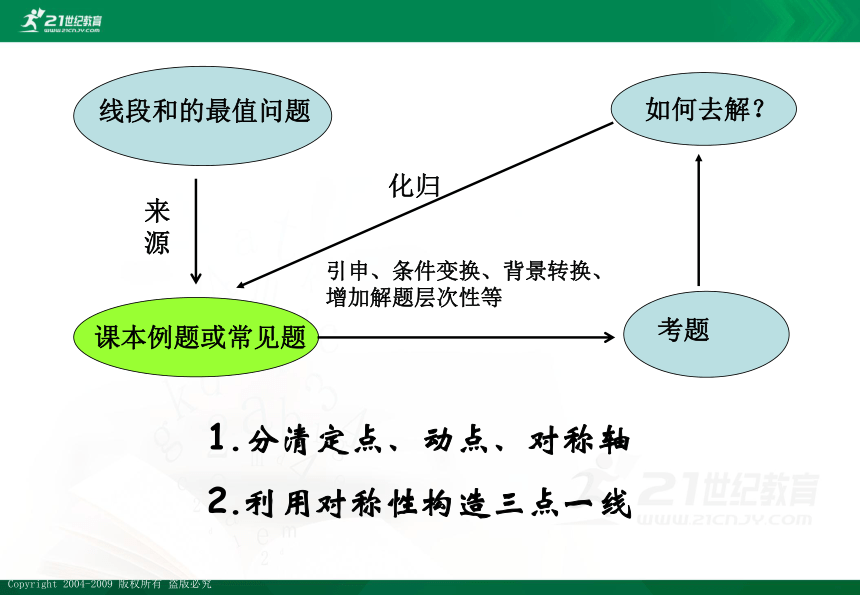
线段和的最值问题
课本例题或常见题
考题
如何去解?
化归
来源
引申、条件变换、背景转换、增加解题层次性等
1.分清定点、动点、对称轴
2.利用对称性构造三点一线
已知抛物线 若一个动点M自P(0,1)出发,先到达对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点F的位置,并求出这个最短路程的长。
y
o
X
1
-1
(0,2)A
(0,1)P
A’(5,2)
F
y
o
X
C
1
-1
(0,2)A
(0,1)P
F
变一变
若一个动点M自P出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点E、点F的位置,并求出这个最短路程的长
E
y
o
X
C
1
-1
(0,2)A
(0,1)P
A’(5,2)
F
若一个动点M自P(0,1)出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点E、点F的位置,并求出这个最短路程的长
E
P’
如图:已知点A(-4,8)和点B(2,n)在抛物线y=ax2上,
(1)求a的值及点B关于X轴对称点P的坐标,并在X轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2 ,记平移后点A的对应点为Aˊ,点B的对应点为Bˊ,点C(-2,0)和D(-4,0)是X轴上的两个定点.
①当抛物线向左平移到某个位置
时,AˊC+CBˊ最短,求
此时抛物线的函数解析式;
②当抛物线向左或向右平移时,
是否存在某个位置,使四边
形AˊBˊCD的周长最短?若
存在求出此时抛物线的解析式;
若不存在,请说明理由。
4
x
2
2
A
8
-2
O
-2
-4
y
6
B
C
D
-4
4
线段和的最值问题
课本例题或常见题
考题
如何去解?
化归:(利用对称性构造三点一线)
来源
引申、条件变换、移植转换、增加解题层次性等
A
B
C
D
M
P
如图,正方形ABCD中,AB=2,
由两个点到多个点,增加层次性
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
点的个数动一动
(3)若M1、M2…M9是AB边上的10等分点, P1、P2…P9依次是对角线AC上任意点,直接写出(P1M1+P1B)2+(P2M1+P2M2)2
+…+(P9M8+P9M9)2的最小值
(2)若M1、M2是AB边上的三等分点, P1、P2依次是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
A
B
C
D
M1
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
P1
如图,正方形ABCD中,AB=2,
(2)若M1、M2是AB边上的三等分点, P1、P2依次是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
M2
P2
点的个数动一动
由两个点到多个点,增加层次性
A
B
C
D
M1
M2
M1’
P1
P2
(P1M1+P1B)2+(P2M1+P2M2)2
M1D2
M1’M22
+
A
B
C
D
M1
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
P1
如图,正方形ABCD中,AB=2,
M2
P2
M9
M8
P9
(3)若M1、M2…M9是AB边上的10等分点, P1、P2…P9依次是对角线AC上任意点,直接写出(P1M1+P1B)2+(P2M1+P2M2)2
+…+(P9M8+P9M9)2的最小值
(2)若M1、M2是AB边上的三等分点, P1、P2是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
点的个数动一动
由两个点到多个点,增加层次性
几何图形中
线段和差的最值问题
冲刺中考
A
P
M
B
C
D
.
.
菱形ABCD中,AB=10,∠BAD=600,
M是边AB上的中点,P是对角线AC上一点.
(1)求PB+PM的最小值.
(2)求PB-PM的最大值,并指出此时点P的位置.
A
B
A’
P
课本原型:如图,要在街道旁修建一个奶站,向居民区 A、B提供牛奶,奶站应建在什么地方,才能使从A,B到它的距离之和最短?
街道
基本解法:利用对称性构 造三点一线
依据:两点之间线段最短
A
B
C
D
M
(1)若M是AB边上的中点,求PM+PB的最小值.
如图,正方形ABCD中,AB=2,P是对角线AC上一点.
P
P
利用对称性构造三点一线
在几何背景下的应用
A
B
C
D
M
点动线不动
(2)若M、N分别是AB,BC边上的点,且AM=CN=1/3AB,求PM+PN的最小值.
P
N
A组变式:点B换成了点N
如图,正方形ABCD中,AB=2,P是对角线AC上一点.
A
B
C
D
(3)连结QC,点P、M是QC、BC上任意点,求PM+PB的最小值。
B组变式:改动了对称轴的位置,点M变成了动点
如图,正方形ABCD中,AB=2,Q是AB中点,
Q
B’
M
P
点线一起动
P
M
线段和的最值问题
课本例题或常见题
考题
如何去解?
化归
来源
引申、条件变换、背景转换、增加解题层次性等
1.分清定点、动点、对称轴
2.利用对称性构造三点一线
已知抛物线 若一个动点M自P(0,1)出发,先到达对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点F的位置,并求出这个最短路程的长。
y
o
X
1
-1
(0,2)A
(0,1)P
A’(5,2)
F
y
o
X
C
1
-1
(0,2)A
(0,1)P
F
变一变
若一个动点M自P出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点E、点F的位置,并求出这个最短路程的长
E
y
o
X
C
1
-1
(0,2)A
(0,1)P
A’(5,2)
F
若一个动点M自P(0,1)出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A。确定使点M运动的总路径最短的点E、点F的位置,并求出这个最短路程的长
E
P’
如图:已知点A(-4,8)和点B(2,n)在抛物线y=ax2上,
(1)求a的值及点B关于X轴对称点P的坐标,并在X轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2 ,记平移后点A的对应点为Aˊ,点B的对应点为Bˊ,点C(-2,0)和D(-4,0)是X轴上的两个定点.
①当抛物线向左平移到某个位置
时,AˊC+CBˊ最短,求
此时抛物线的函数解析式;
②当抛物线向左或向右平移时,
是否存在某个位置,使四边
形AˊBˊCD的周长最短?若
存在求出此时抛物线的解析式;
若不存在,请说明理由。
4
x
2
2
A
8
-2
O
-2
-4
y
6
B
C
D
-4
4
线段和的最值问题
课本例题或常见题
考题
如何去解?
化归:(利用对称性构造三点一线)
来源
引申、条件变换、移植转换、增加解题层次性等
A
B
C
D
M
P
如图,正方形ABCD中,AB=2,
由两个点到多个点,增加层次性
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
点的个数动一动
(3)若M1、M2…M9是AB边上的10等分点, P1、P2…P9依次是对角线AC上任意点,直接写出(P1M1+P1B)2+(P2M1+P2M2)2
+…+(P9M8+P9M9)2的最小值
(2)若M1、M2是AB边上的三等分点, P1、P2依次是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
A
B
C
D
M1
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
P1
如图,正方形ABCD中,AB=2,
(2)若M1、M2是AB边上的三等分点, P1、P2依次是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
M2
P2
点的个数动一动
由两个点到多个点,增加层次性
A
B
C
D
M1
M2
M1’
P1
P2
(P1M1+P1B)2+(P2M1+P2M2)2
M1D2
M1’M22
+
A
B
C
D
M1
(1)若M是AB边上的中点, P是对角线AC上任意一点,求(PM+PB)2的最小值
P1
如图,正方形ABCD中,AB=2,
M2
P2
M9
M8
P9
(3)若M1、M2…M9是AB边上的10等分点, P1、P2…P9依次是对角线AC上任意点,直接写出(P1M1+P1B)2+(P2M1+P2M2)2
+…+(P9M8+P9M9)2的最小值
(2)若M1、M2是AB边上的三等分点, P1、P2是对角线AC上任意两点,求(P1M1+P1B)2+(P2M1+P2M2)2的最小值
点的个数动一动
由两个点到多个点,增加层次性
同课章节目录
