2.3.2 角平分线的性质及作图同步练习题(含答案)
文档属性
| 名称 | 2.3.2 角平分线的性质及作图同步练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-26 20:40:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
3 简单的轴对称图形
第2课时 角平分线的性质及作图
夯实基础
知识点一 角平分线的性质
1.如图,点P是∠BAC的角平分线AD上一点,PE⊥AB于点E,PF⊥AC于点F,则下列结论中不正确的是( )
A. PE=PF B.AE=AF C.△APE≌△APF D.AP=PE+PF
2.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB,垂足为点E,请任意写出一组相等的线段_________________________。
知识点二 作角的平分线
3.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
A. SSS B. SAS C. ASA D. AAS
4.如图,已知∠AOB和C,D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等。
易错点 运用角平分线的性质时,常因忽略“到角两边的距离”而导致错误
5.如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD>DE B.AD=DE C.AD<DE D.不确定
能力提升
6.如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB,垂足为点E,则下面结论中错误的是( )
A. AD+DE=AC B. DB平分∠EDC C. DE平分∠ADB D. DC+BE>BD
7.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A. 8 B. 6 C. 4 D. 2
8.(东营中考)如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是___________。
9.如图,已知四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠BAD+∠C=________?.
10.在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是___________。
11.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP长的最小值为____________。
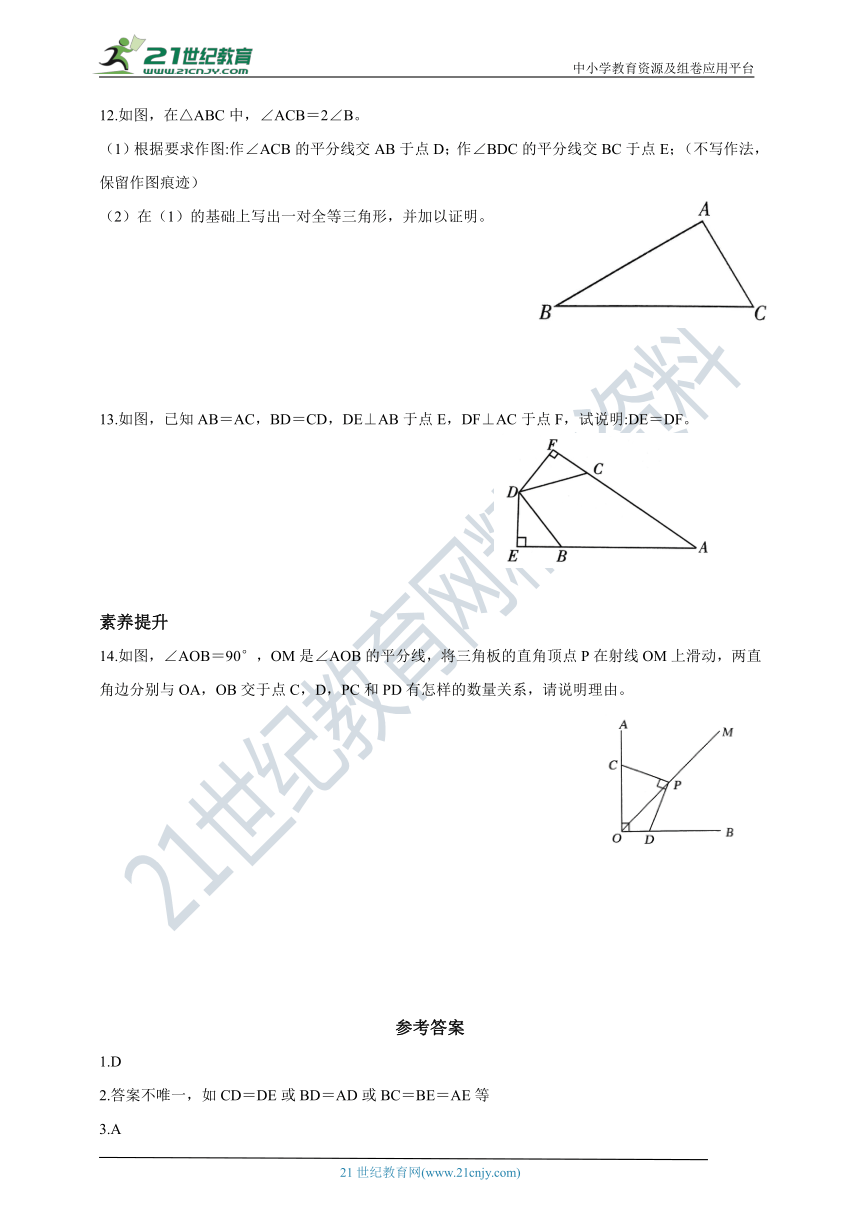
12.如图,在△ABC中,∠ACB=2∠B。
(1)根据要求作图:作∠ACB的平分线交AB于点D;作∠BDC的平分线交BC于点E;(不写作法,保留作图痕迹)
(2)在(1)的基础上写出一对全等三角形,并加以证明。
13.如图,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试说明:DE=DF。
素养提升
14.如图,∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,PC和PD有怎样的数量关系,请说明理由。
参考答案
1.D
2.答案不唯一,如CD=DE或BD=AD或BC=BE=AE等
3.A
4.解:如图,连接CD,作CD的中垂线和∠AOB的平分线,两线的交点即为所求作的点P.
5.D 【解析】本题易出错误原因是误认为角平分线上点与角两边上的任意一点连接的线段都相等,而忽略了“到角两边距离”这一条件,即忽略DE与BC,AB与AD是否垂直,从而错选B
6.C
7.C 【解析】如图,过点P作PE⊥BC于点E.因为AB∥CD,PA⊥AB,所以PD⊥CD.因为BP和CP分别平分∠ABC和∠DCB,所以PA=PE,PD=PE.所以PE=PA=PD.因为p+D=AD=8,所以PA=PD=4,所以PE=4.
8.15 【解析】由作图知CD是∠ACB的平分线,所以点D到∠ACB两边的距离相等又因为∠B=90°,BD=3所以点D到AC边的距离为3.所以△ACD的面积=×10×3=15.
9. 180 10. 4:3 11. 3
12.解:(1)如图所示。
(2)△BDE≌△CDE.
证明:因为CD平分∠ACB,所以∠DCE=∠ACB。
又因为∠ACB=2∠B,所以∠B=∠DCE.
因为DE平分∠BDC,所以∠BDE=∠CDE.
又因为DE=DE,所以△BDE≌△CDE(AAS)
13.解:如图,连接AD。
因为AB=AC,BD=CD,AD=AD,所以△ABD≌△ACD(SSS)
所以∠BAD=∠CAD,即AD是∠EAF的平分线。
又因为DE⊥AB,DF⊥AC,所以DE=DF.
14.解:PC=PD.理由如下:
如图,过点P分别作PE⊥OB于点E,PF⊥OA于点F,则∠CFP=∠DEP=90°。
因为OM是∠AOB的平分线,所以PF=PE。
因为∠1+∠FPD=90°,∠AOB=90°,所以∠FPE=90°。所以∠2+∠FPD=90°所以∠1=∠2.
在△CFP和△DEP中,因为∠CFP=∠DEP,PF=PE,∠1=∠2,所以△CFP≌△DEP(ASA)。
所以PC=PD.
_21?????????è?????(www.21cnjy.com)_
第二章 轴对称
3 简单的轴对称图形
第2课时 角平分线的性质及作图
夯实基础
知识点一 角平分线的性质
1.如图,点P是∠BAC的角平分线AD上一点,PE⊥AB于点E,PF⊥AC于点F,则下列结论中不正确的是( )
A. PE=PF B.AE=AF C.△APE≌△APF D.AP=PE+PF
2.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB,垂足为点E,请任意写出一组相等的线段_________________________。
知识点二 作角的平分线
3.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
A. SSS B. SAS C. ASA D. AAS
4.如图,已知∠AOB和C,D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等。
易错点 运用角平分线的性质时,常因忽略“到角两边的距离”而导致错误
5.如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD>DE B.AD=DE C.AD<DE D.不确定
能力提升
6.如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB,垂足为点E,则下面结论中错误的是( )
A. AD+DE=AC B. DB平分∠EDC C. DE平分∠ADB D. DC+BE>BD
7.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A. 8 B. 6 C. 4 D. 2
8.(东营中考)如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是___________。
9.如图,已知四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠BAD+∠C=________?.
10.在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是___________。
11.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP长的最小值为____________。
12.如图,在△ABC中,∠ACB=2∠B。
(1)根据要求作图:作∠ACB的平分线交AB于点D;作∠BDC的平分线交BC于点E;(不写作法,保留作图痕迹)
(2)在(1)的基础上写出一对全等三角形,并加以证明。
13.如图,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试说明:DE=DF。
素养提升
14.如图,∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,PC和PD有怎样的数量关系,请说明理由。
参考答案
1.D
2.答案不唯一,如CD=DE或BD=AD或BC=BE=AE等
3.A
4.解:如图,连接CD,作CD的中垂线和∠AOB的平分线,两线的交点即为所求作的点P.
5.D 【解析】本题易出错误原因是误认为角平分线上点与角两边上的任意一点连接的线段都相等,而忽略了“到角两边距离”这一条件,即忽略DE与BC,AB与AD是否垂直,从而错选B
6.C
7.C 【解析】如图,过点P作PE⊥BC于点E.因为AB∥CD,PA⊥AB,所以PD⊥CD.因为BP和CP分别平分∠ABC和∠DCB,所以PA=PE,PD=PE.所以PE=PA=PD.因为p+D=AD=8,所以PA=PD=4,所以PE=4.
8.15 【解析】由作图知CD是∠ACB的平分线,所以点D到∠ACB两边的距离相等又因为∠B=90°,BD=3所以点D到AC边的距离为3.所以△ACD的面积=×10×3=15.
9. 180 10. 4:3 11. 3
12.解:(1)如图所示。
(2)△BDE≌△CDE.
证明:因为CD平分∠ACB,所以∠DCE=∠ACB。
又因为∠ACB=2∠B,所以∠B=∠DCE.
因为DE平分∠BDC,所以∠BDE=∠CDE.
又因为DE=DE,所以△BDE≌△CDE(AAS)
13.解:如图,连接AD。
因为AB=AC,BD=CD,AD=AD,所以△ABD≌△ACD(SSS)
所以∠BAD=∠CAD,即AD是∠EAF的平分线。
又因为DE⊥AB,DF⊥AC,所以DE=DF.
14.解:PC=PD.理由如下:
如图,过点P分别作PE⊥OB于点E,PF⊥OA于点F,则∠CFP=∠DEP=90°。
因为OM是∠AOB的平分线,所以PF=PE。
因为∠1+∠FPD=90°,∠AOB=90°,所以∠FPE=90°。所以∠2+∠FPD=90°所以∠1=∠2.
在△CFP和△DEP中,因为∠CFP=∠DEP,PF=PE,∠1=∠2,所以△CFP≌△DEP(ASA)。
所以PC=PD.
_21?????????è?????(www.21cnjy.com)_
