宿迁市2011届高三数学130分训练(8)
文档属性
| 名称 | 宿迁市2011届高三数学130分训练(8) |
|
|
| 格式 | zip | ||
| 文件大小 | 38.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-24 00:00:00 | ||
图片预览

文档简介
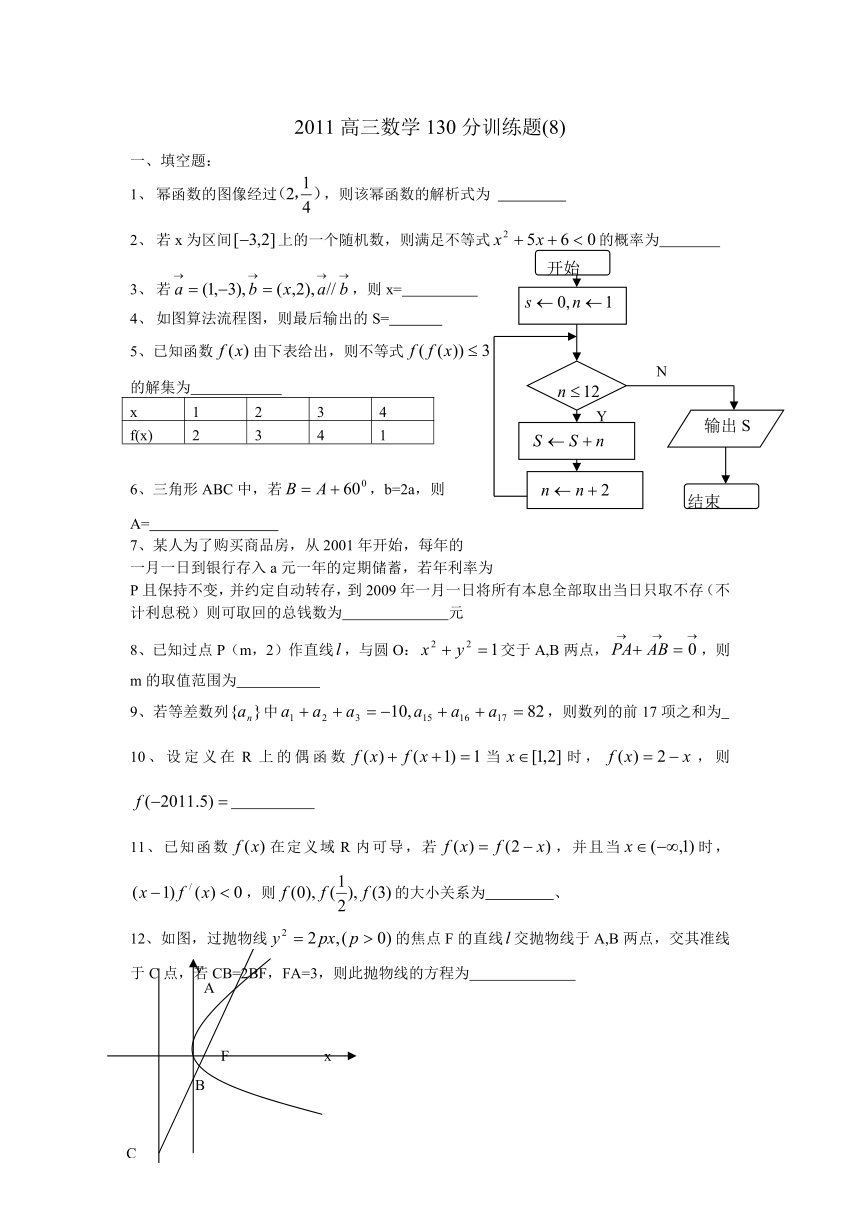
2011高三数学130分训练题(8)
填空题:
幂函数的图像经过,则该幂函数的解析式为
若x为区间上的一个随机数,则满足不等式的概率为
若,则x=
如图算法流程图,则最后输出的S=
5、已知函数由下表给出,则不等式
的解集为
x 1 2 3 4
f(x) 2 3 4 1
6、三角形ABC中,若,b=2a,则
A=
7、某人为了购买商品房,从2001年开始,每年的
一月一日到银行存入a元一年的定期储蓄,若年利率为
P且保持不变,并约定自动转存,到2009年一月一日将所有本息全部取出当日只取不存(不计利息税)则可取回的总钱数为 元
8、已知过点P(m,2)作直线,与圆O:交于A,B两点,,则m的取值范围为
9、若等差数列中,则数列的前17项之和为
10、设定义在R上的偶函数当时,,则
11、已知函数在定义域R内可导,若,并且当时,,则的大小关系为 、
12、如图,过抛物线的焦点F的直线交抛物线于A,B两点,交其准线于C点,若CB=2BF,FA=3,则此抛物线的方程为
13、已知函数对于任意实数x,和g(x)的值至少一个为正数,则实数m的取值范围为
14、设函数的定义域为D,若存在非零实数,使得对于任意,有,且,则称为M上的高调函数,若定义域为的函数为上的m高调函数,则实数m的取值范围为
解答题:
15、若,其中,,,(1)求:的最小正周期
(2)若且,求的值
16、如图在三棱柱中,每个侧面都是边长为2的正方形,为AB的中点,E为的中点,的交点为O(1)求证:(2)求点A到平面的距离
17、如图A为圆形纸片不同于圆心C的定点,动点M在圆周上,将圆形纸片折起,使得点M与点A重合,设折痕m交线段CM于点N,将圆形纸片放在平面直角坐标系中,设,A(1,0),记N点的轨迹方程为E
(1)求证E点轨迹为椭圆,并求出当时的椭圆的标准方程。
(2)设直线过点C和椭圆E上顶点,点A关于直线对称的点为Q,若椭圆E的离心率,求:点Q的纵坐标的取值范围。
18、已知数列中,=1其前n项和为,当时,(1)求证:为等比数列;(2)求数列的通项公式;(3)若,数列的前n项和为,,问是否存在正整数n,使得等式成立?若存在求出相应的n的值和的值,若不存在说明理由。
开始
结束
输出S
N
Y
C
B
A
F
x
y
A
B
C
O
E
D
M
C
A
N
m
y
x
O
填空题:
幂函数的图像经过,则该幂函数的解析式为
若x为区间上的一个随机数,则满足不等式的概率为
若,则x=
如图算法流程图,则最后输出的S=
5、已知函数由下表给出,则不等式
的解集为
x 1 2 3 4
f(x) 2 3 4 1
6、三角形ABC中,若,b=2a,则
A=
7、某人为了购买商品房,从2001年开始,每年的
一月一日到银行存入a元一年的定期储蓄,若年利率为
P且保持不变,并约定自动转存,到2009年一月一日将所有本息全部取出当日只取不存(不计利息税)则可取回的总钱数为 元
8、已知过点P(m,2)作直线,与圆O:交于A,B两点,,则m的取值范围为
9、若等差数列中,则数列的前17项之和为
10、设定义在R上的偶函数当时,,则
11、已知函数在定义域R内可导,若,并且当时,,则的大小关系为 、
12、如图,过抛物线的焦点F的直线交抛物线于A,B两点,交其准线于C点,若CB=2BF,FA=3,则此抛物线的方程为
13、已知函数对于任意实数x,和g(x)的值至少一个为正数,则实数m的取值范围为
14、设函数的定义域为D,若存在非零实数,使得对于任意,有,且,则称为M上的高调函数,若定义域为的函数为上的m高调函数,则实数m的取值范围为
解答题:
15、若,其中,,,(1)求:的最小正周期
(2)若且,求的值
16、如图在三棱柱中,每个侧面都是边长为2的正方形,为AB的中点,E为的中点,的交点为O(1)求证:(2)求点A到平面的距离
17、如图A为圆形纸片不同于圆心C的定点,动点M在圆周上,将圆形纸片折起,使得点M与点A重合,设折痕m交线段CM于点N,将圆形纸片放在平面直角坐标系中,设,A(1,0),记N点的轨迹方程为E
(1)求证E点轨迹为椭圆,并求出当时的椭圆的标准方程。
(2)设直线过点C和椭圆E上顶点,点A关于直线对称的点为Q,若椭圆E的离心率,求:点Q的纵坐标的取值范围。
18、已知数列中,=1其前n项和为,当时,(1)求证:为等比数列;(2)求数列的通项公式;(3)若,数列的前n项和为,,问是否存在正整数n,使得等式成立?若存在求出相应的n的值和的值,若不存在说明理由。
开始
结束
输出S
N
Y
C
B
A
F
x
y
A
B
C
O
E
D
M
C
A
N
m
y
x
O
同课章节目录
