人教版九年级上册数学24.1.4圆周角定理的推论课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册数学24.1.4圆周角定理的推论课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-26 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
圆周角定理的
推论
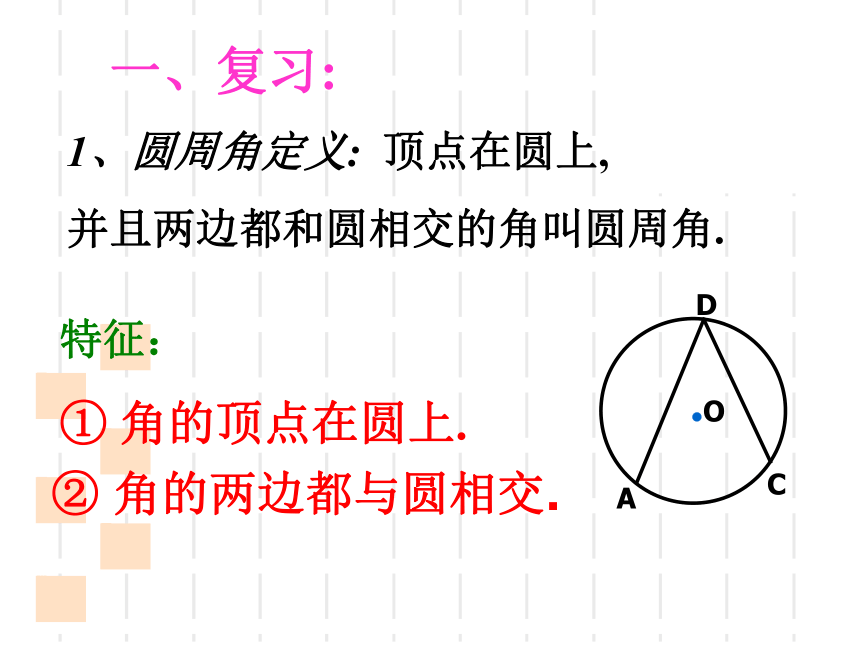
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
1、圆周角定义:
顶点在圆上,
并且两边都和圆相交的角叫圆周角.
一、复习:
A
C
D
(1)圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
(2)圆周角度数定理:
圆周角的度数等于它所对的弧的度数一半。
圆心角的度数等于它所对的弧的度数。
自学指导
内容:课本41---43页内容
时间:5分钟
方法:独立自学
要求:自学后完成下列讨论并回答下列问题
(1)圆周角定理有哪些推论
(2)完成自学检测
问题讨论
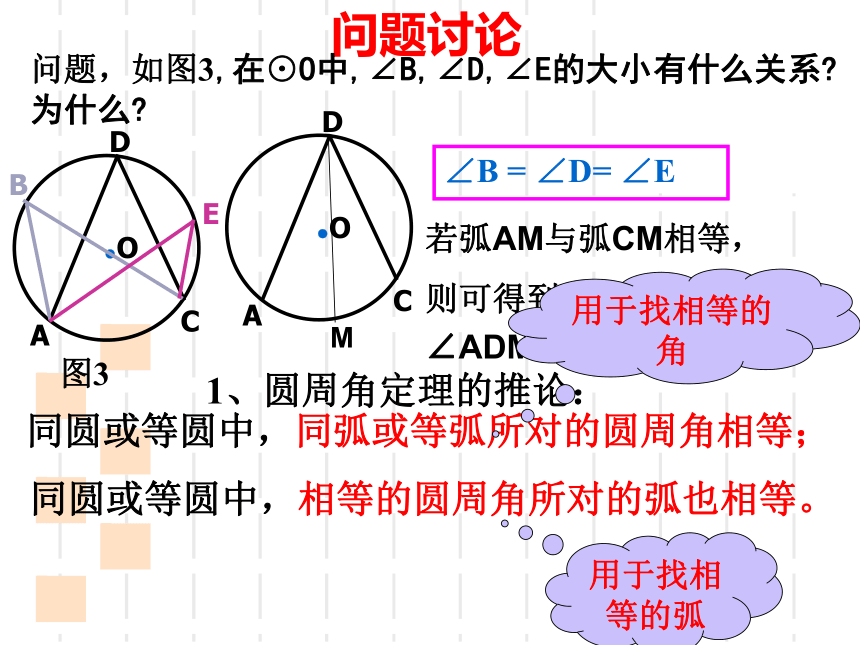
问题,如图3,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
图3
∠B
=
∠D=
∠E
M
若弧AM与弧CM相等,
则可得到什么结论?
∠ADM=
∠CDM
1、圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
用于找相等的角
用于找相等的弧
同圆或等圆中,相等的圆周角所对的弧也相等。
第2课时 圆周角定理的推论
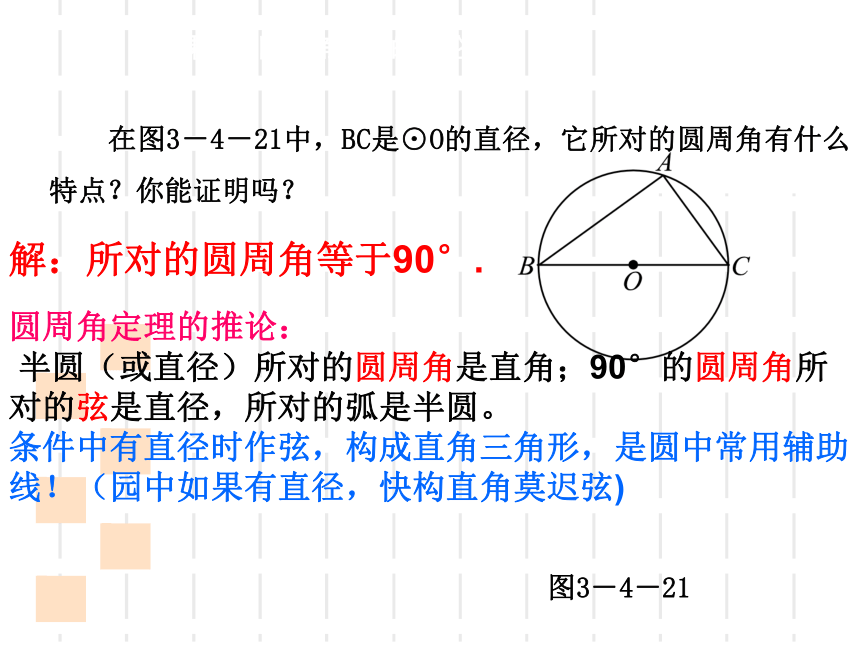
在图3-4-21中,BC是⊙O的直径,它所对的圆周角有什么特点?你能证明吗?
图3-4-21
解:所对的圆周角等于90°.
圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径,所对的弧是半圆。
条件中有直径时作弦,构成直角三角形,是圆中常用辅助线!(园中如果有直径,快构直角莫迟弦)
辨一辨
图3
M
圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
1、同弧或等弧所对的圆周角相等?
2、相等的圆周角所对的弧也相等?
3、同圆或等圆中,一条弦或相等的两条弦所对的圆周角相等?
对
错
错
正确结论:同圆或等圆中,一条弦或相等的两条弦所对的圆周角相等或互补
第2课时 圆周角定理的推论
?
知识点二 圆内接四边形及四边形的外接圆
如果一个四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.
第2课时 圆周角定理的推论
?
知识点三 圆内接四边形的性质
圆内接四边形的对角互补.外角等于内对角
[拓展]
圆内接四边形的对角相等,则此时的四边形是——
(1)圆内接平行四边形是------
(2)圆内接菱形是——--
(3)圆内接梯形是---------
矩形
矩形
正方形
等腰梯形
自学检测:
·
·
C
D
A
B
O
1
2
3
如图,四边形ABCD内接于⊙O.找出图中分别与∠1,
∠2
,∠3相等的角.
4
5
6
7
8
引伸1:若BD=AC,则还可以得到哪些相等关系?
E
引伸2:若∠5=∠2=600,还可以得到哪些600角?
BD=AC
∠3=∠
5
=∠4=∠
7
DE=AE,CE=BE
AB=CD
∠DCB=∠ABC
2:
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°.
求证:△ABC是等边三角形
·
·
A
P
B
C
O
∴∠1=∠APC=60°
(同弧所对的圆周角相等)
∴∠2=∠CPB=60°。
∴△ABC等边三角形。
1
2
∴∠1=∠2=600
45°或135°
3、弦AB分圆周成两部分,其中一部分是另一部分的3倍,则弦AB所对的圆周角∠ACB
度数为________。
若圆的半径为2,则△
ACB面积的最大值是______
2√2+2
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
即
AD⊥BC,
∵AB=AC,
∴∠1=∠2,
(在同圆中,相等的圆周角所对的弧相等).
O.
当堂训练
1
2
当堂训练
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
若∠B=70?,求弧BD的度数?
你还能求哪些弧的度数?
O
若∠B=70?,求弧AE的度数?
当堂训练
O
若∠B=70?,求弧AE的度数?
①
②
③
图③是用了转化思想
图①辅助线是作半径OE构成等腰△AOE,转化成求∠AOE问题
图②辅助线是由条件中的直径AB想到作弦BE
构成Rt△ABE,转化成求∠ABE
当堂训练:
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,(即称这个区域为弓形ACB)C表示一个危险临界点,∠ACB就是“危险角”
弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?
500
1
设AP与弓形交于点E
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?
α
α
Q
F
α
当∠P<
∠α时,…,船P在弓形外,…
当∠P>
∠α时,…,船Q在弓形内,…
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
O
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
D
O
归纳总结
本节课你学习了哪些内容?
圆周角定理的
推论
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
1、圆周角定义:
顶点在圆上,
并且两边都和圆相交的角叫圆周角.
一、复习:
A
C
D
(1)圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
(2)圆周角度数定理:
圆周角的度数等于它所对的弧的度数一半。
圆心角的度数等于它所对的弧的度数。
自学指导
内容:课本41---43页内容
时间:5分钟
方法:独立自学
要求:自学后完成下列讨论并回答下列问题
(1)圆周角定理有哪些推论
(2)完成自学检测
问题讨论
问题,如图3,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
图3
∠B
=
∠D=
∠E
M
若弧AM与弧CM相等,
则可得到什么结论?
∠ADM=
∠CDM
1、圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
用于找相等的角
用于找相等的弧
同圆或等圆中,相等的圆周角所对的弧也相等。
第2课时 圆周角定理的推论
在图3-4-21中,BC是⊙O的直径,它所对的圆周角有什么特点?你能证明吗?
图3-4-21
解:所对的圆周角等于90°.
圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径,所对的弧是半圆。
条件中有直径时作弦,构成直角三角形,是圆中常用辅助线!(园中如果有直径,快构直角莫迟弦)
辨一辨
图3
M
圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
1、同弧或等弧所对的圆周角相等?
2、相等的圆周角所对的弧也相等?
3、同圆或等圆中,一条弦或相等的两条弦所对的圆周角相等?
对
错
错
正确结论:同圆或等圆中,一条弦或相等的两条弦所对的圆周角相等或互补
第2课时 圆周角定理的推论
?
知识点二 圆内接四边形及四边形的外接圆
如果一个四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆.
第2课时 圆周角定理的推论
?
知识点三 圆内接四边形的性质
圆内接四边形的对角互补.外角等于内对角
[拓展]
圆内接四边形的对角相等,则此时的四边形是——
(1)圆内接平行四边形是------
(2)圆内接菱形是——--
(3)圆内接梯形是---------
矩形
矩形
正方形
等腰梯形
自学检测:
·
·
C
D
A
B
O
1
2
3
如图,四边形ABCD内接于⊙O.找出图中分别与∠1,
∠2
,∠3相等的角.
4
5
6
7
8
引伸1:若BD=AC,则还可以得到哪些相等关系?
E
引伸2:若∠5=∠2=600,还可以得到哪些600角?
BD=AC
∠3=∠
5
=∠4=∠
7
DE=AE,CE=BE
AB=CD
∠DCB=∠ABC
2:
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°.
求证:△ABC是等边三角形
·
·
A
P
B
C
O
∴∠1=∠APC=60°
(同弧所对的圆周角相等)
∴∠2=∠CPB=60°。
∴△ABC等边三角形。
1
2
∴∠1=∠2=600
45°或135°
3、弦AB分圆周成两部分,其中一部分是另一部分的3倍,则弦AB所对的圆周角∠ACB
度数为________。
若圆的半径为2,则△
ACB面积的最大值是______
2√2+2
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
即
AD⊥BC,
∵AB=AC,
∴∠1=∠2,
(在同圆中,相等的圆周角所对的弧相等).
O.
当堂训练
1
2
当堂训练
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
若∠B=70?,求弧BD的度数?
你还能求哪些弧的度数?
O
若∠B=70?,求弧AE的度数?
当堂训练
O
若∠B=70?,求弧AE的度数?
①
②
③
图③是用了转化思想
图①辅助线是作半径OE构成等腰△AOE,转化成求∠AOE问题
图②辅助线是由条件中的直径AB想到作弦BE
构成Rt△ABE,转化成求∠ABE
当堂训练:
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,(即称这个区域为弓形ACB)C表示一个危险临界点,∠ACB就是“危险角”
弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?
500
1
设AP与弓形交于点E
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?
α
α
Q
F
α
当∠P<
∠α时,…,船P在弓形外,…
当∠P>
∠α时,…,船Q在弓形内,…
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
O
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
D
O
归纳总结
本节课你学习了哪些内容?
同课章节目录
